Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 1
1. Понятие матрицы. Виды матриц.
2. Угол между прямыми в пространстве.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Какая из следующих функций имеет производную  а) у=6х; б) у=х3+1; в) у=3; г) у=0
Вычислить
а) у=6х; б) у=х3+1; в) у=3; г) у=0
Вычислить  Решить систему уравнений по правилу Крамера
Решить систему уравнений по правилу Крамера  Записать в тригонометрической форме комплексное число 1+i.
Найти периметр треугольника с вершинами А(3, –2, 8), В(–1, 0, 6), С(5, 1, –7).
Записать в тригонометрической форме комплексное число 1+i.
Найти периметр треугольника с вершинами А(3, –2, 8), В(–1, 0, 6), С(5, 1, –7).
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 2
1. Метод Гаусcа.
2. Различные способы задания прямой в пространстве.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Какое из соотношений для множеств является верным:
а) 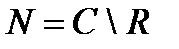 ; б) ; б)  ; в) ; в)  ; г) ; г)  .
Значение выражения .
Значение выражения  равно:
а) 3; б) 35; в) 6; г) другой ответ.
Решить систему уравнений: равно:
а) 3; б) 35; в) 6; г) другой ответ.
Решить систему уравнений:  Записать число z=5i в тригонометрической и показательной формах.
Найти
Записать число z=5i в тригонометрической и показательной формах.
Найти 
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 3
1. Линейные операции над матрицами.
2. Теоремы Ролля, Лагранжа, Коши.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Производной функции у=3х2 является:
а) х3; б) 6х; в) 6х2; г) другой ответ.
Вычислить: i15+i24–i2
Решить систему по правилу Крамера 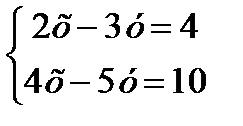 Найти
Найти  Найти центр, оси, вершины, фокусы, эксцентриситет и асимптоты гиперболы 5х2–4у2+30х+8у+21=0
Найти центр, оси, вершины, фокусы, эксцентриситет и асимптоты гиперболы 5х2–4у2+30х+8у+21=0
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 4
1. Метод обратной матрицы для решения системы линейных уравнений.
2. Окружность, ее геометрические свойства и уравнения.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Какое из соотношений для множеств является верным:
а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  Составить уравнение прямой, проходящей через точку В(5; 3;1) и имеющей нормальный вектор
Составить уравнение прямой, проходящей через точку В(5; 3;1) и имеющей нормальный вектор  .
Решить уравнение на множестве комплексных чисел: х2+4х+5=0
Используя формулу Муавра, найти z6, если .
Решить уравнение на множестве комплексных чисел: х2+4х+5=0
Используя формулу Муавра, найти z6, если  Найдите вектор
Найдите вектор  из системы уравнений из системы уравнений 
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 5
1. Определитель 2-ого порядка и его вычисления.
2. Предел функции в точке и на бесконечности.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Укажите, чему равна  , если , если  а) –10; б) 10; в) 110; г) другой ответ
Вычислить
а) –10; б) 10; в) 110; г) другой ответ
Вычислить  Найдите
Найдите  , если , если  Решить уравнение
Решить уравнение 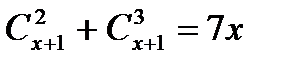 Найти центр, оси, вершины, фокусы, эксцентриситет эллипса 9х2 + 10у2 + 40у – 50 = 0
Найти центр, оси, вершины, фокусы, эксцентриситет эллипса 9х2 + 10у2 + 40у – 50 = 0
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 6
1. Элементарные преобразования матрицы. Транспонирование матрицы.
2. Взаимное расположение прямой и плоскости в пространстве.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Определитель  равен:
а) 5; б) –7; в) 8; г) другой ответ.
Составить уравнение прямой, проходящей через начало координат и точку М (1, 2, –3).
Найти х, если равен:
а) 5; б) –7; в) 8; г) другой ответ.
Составить уравнение прямой, проходящей через начало координат и точку М (1, 2, –3).
Найти х, если  Точка движется прямолинейно по закону
Точка движется прямолинейно по закону  . В какой момент времени ее скорость окажется равной нулю?
Найти центр, оси, вершины, эксцентриситет и асимптоты гиперболы: 16х2 – 9у2 –64х –54у – 161 = 0 . В какой момент времени ее скорость окажется равной нулю?
Найти центр, оси, вершины, эксцентриситет и асимптоты гиперболы: 16х2 – 9у2 –64х –54у – 161 = 0
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ