предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 7
1. Обратная матрица и ее построение.
2. Расстояние от точки до прямой в пространстве.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Производная функции у = 4(х2–1) равна:
а) 4х2; б) 4; в) 8х; г) 8х–4.
Вычислить:  Решите уравнение:
Решите уравнение:  Найти координаты вершин, оси, фокусы, эксцентриситет гиперболы 4х2 – 5у2 – 100 = 0
Найдите вектор
Найти координаты вершин, оси, фокусы, эксцентриситет гиперболы 4х2 – 5у2 – 100 = 0
Найдите вектор 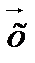 , зная, что он ортогонален векторам , зная, что он ортогонален векторам  и удовлетворяет уравнению и удовлетворяет уравнению 
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 8
.
1. Дифференциал функции и его применение в приближенных вычислениях.
2. Парабола, ее геометрические свойства и уравнение.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Производная функции  равна:
а) 2 cos 2x; б) 2 cos x; в) 4 cos 2x; г) 4 sin 2x.
Составить уравнение прямой, проходящей через начало координат перпендикулярно вектору а (1,-2,3).
Решить уравнение на множестве комплексных чисел: х2 + 4х + 5 = 0
Найти углы треугольника, заданного вершинами А(–6, –3;0), В(6, 7;1), С(2, –1;1)
Если система равна:
а) 2 cos 2x; б) 2 cos x; в) 4 cos 2x; г) 4 sin 2x.
Составить уравнение прямой, проходящей через начало координат перпендикулярно вектору а (1,-2,3).
Решить уравнение на множестве комплексных чисел: х2 + 4х + 5 = 0
Найти углы треугольника, заданного вершинами А(–6, –3;0), В(6, 7;1), С(2, –1;1)
Если система  имеет решение (1; 1), то разность а–в равна:
а) 0; б) 4; в) –4; г) –3; д) 3. имеет решение (1; 1), то разность а–в равна:
а) 0; б) 4; в) –4; г) –3; д) 3.
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 9
1. Определитель 3-ого порядка и его вычисление по правилу треугольника.
2. Эллипс, его геометрические свойства и уравнение.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Чему равна производная функции  а) sin 2x; б) – sin2x; в) cos 2x; г) другой ответ.
Найдите длину вектора
а) sin 2x; б) – sin2x; в) cos 2x; г) другой ответ.
Найдите длину вектора  , если , если  , ,  .
Составьте уравнение средней линии треугольника с вершинами А(5, –2,0), В(1, 6,0), С(–3, 2,0) параллельной стороне ВС.
Найти произведение А . В, если .
Составьте уравнение средней линии треугольника с вершинами А(5, –2,0), В(1, 6,0), С(–3, 2,0) параллельной стороне ВС.
Найти произведение А . В, если  Найдите все значения а, при которых
Найдите все значения а, при которых  для для  , если , если 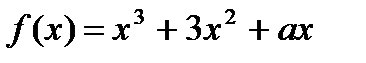
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 10
1. Линейная система 3-ого порядка.
2. Смешанное произведение векторов и его свойства.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Какая из функций имеет производную  а)
а)  ; б) ; б)  ; в) ; в)  ; г) другой ответ.
Вычислить ; г) другой ответ.
Вычислить 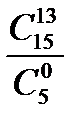 Составьте уравнение эллипса, фокусы которого имеют координаты
Составьте уравнение эллипса, фокусы которого имеют координаты  , а малая ось равна 14.
Найдите внутренние углы треугольника с вершинами А(3; –7,0), В(–1, 4,0), С(–6, –5,0).
Вычислить определитель: , а малая ось равна 14.
Найдите внутренние углы треугольника с вершинами А(3; –7,0), В(–1, 4,0), С(–6, –5,0).
Вычислить определитель: 
|
Преподаватель: _______________
Министерство сельского хозяйства и продовольствия РБ
УО «Столинский государственный аграрно-экономический колледж»
предмет Математика учебный год 2014 / 2015 сессия зимняя
БИЛЕТ № 11
1. Дифференцирование сложной функции.
2. Тригонометрическая форма комплексных чисел, их геометрическая интерпритация.
3.
| Уровень сложности | Кол-во баллов | Задания |
| I II III IV V | Чему равно  , если , если  :
а) –2, б) 2, в) 1, г) другой ответ.
Найдите длину вектора :
а) –2, б) 2, в) 1, г) другой ответ.
Найдите длину вектора  , если , если  , ,  Найдите
Найдите  Найдите значение х и у из равенства
Найдите значение х и у из равенства  Составить уравнение эллипса, найти его эксцентриситет, если расстояние между концами полуосей эллипса равно
Составить уравнение эллипса, найти его эксцентриситет, если расстояние между концами полуосей эллипса равно 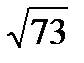 , а разность полуосей а – в = 5. Построить график. , а разность полуосей а – в = 5. Построить график.
|
Преподаватель: _______________