В данном разделе мы докажем некоторые критерии разрешимых, метанильпотентных, дисперсивных по Оре и сверхразрешимых групп в терминах слабо нормальных подгрупп.
Следующая теорема доказывается аналогично теореме 3.5.1.
Группа  разрешима тогда и только тогда, когда
разрешима тогда и только тогда, когда  , где
, где 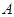 ,
,  - подгруппы группы
- подгруппы группы  такие, что каждая максимальная подгруппа из
такие, что каждая максимальная подгруппа из  и каждая максимальная подгруппа из
и каждая максимальная подгруппа из  слабо нормальны в
слабо нормальны в  .
.
Пусть  - группа тогда следующие утверждения эквивалентны:
- группа тогда следующие утверждения эквивалентны:
(1)  - разрешима;
- разрешима;
(2)  , где
, где  ,
,  - подгруппы группы
- подгруппы группы  такие, что каждая максимальная подгруппа из
такие, что каждая максимальная подгруппа из  и каждая максимальная подгруппа из
и каждая максимальная подгруппа из  слабо квазинормальны в
слабо квазинормальны в  ;
;
(3)  , где
, где  ,
,  - подгруппы группы
- подгруппы группы  такие, что каждая максимальная подгруппа из
такие, что каждая максимальная подгруппа из  и каждая максимальная подгруппа из
и каждая максимальная подгруппа из  слабо нормальны в
слабо нормальны в  .
.
Группа  метанильпотентна тогда и только тогда, когда
метанильпотентна тогда и только тогда, когда  , где подгруппа
, где подгруппа 
 -квазинормальна в
-квазинормальна в  ,
,  - нильпотентна и каждая силовская подгруппа из
- нильпотентна и каждая силовская подгруппа из  слабо нормальна в
слабо нормальна в  .
.
Доказательство. Допустим, что  , где
, где  -
-  -квазинормальна в
-квазинормальна в  ,
,  - нильпотентна и каждая силовская подгруппа из
- нильпотентна и каждая силовская подгруппа из  слабо нормальна в
слабо нормальна в  . Покажем, что группа
. Покажем, что группа  метанильпотентна. Предположим, что это не верно и пусть
метанильпотентна. Предположим, что это не верно и пусть  - контрпример минимального порядка. Тогда справедливы следующие утверждения.
- контрпример минимального порядка. Тогда справедливы следующие утверждения.
(1)  не является нильпотентной группой.
не является нильпотентной группой.
Предположим, что  нильпотентна. Так как ввиду леммы (3),
нильпотентна. Так как ввиду леммы (3), 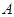 субнормальна, то
субнормальна, то  содержится в некоторой нильпотентной нормальной подгруппе
содержится в некоторой нильпотентной нормальной подгруппе  из
из  по лемме (2). Тогда
по лемме (2). Тогда

нильпотентна и поэтому  метанильпотентна. Полученное противоречие с выбором группы
метанильпотентна. Полученное противоречие с выбором группы  доказывает (1).
доказывает (1).
(2)  .
.
Допустим, что  . Тогда ввиду леммы,
. Тогда ввиду леммы,  нильпотентна, что противоречит (1). Значит, мы имеем (2).
нильпотентна, что противоречит (1). Значит, мы имеем (2).
(3) Если  - абелева минимальная нормальная подгруппа группы
- абелева минимальная нормальная подгруппа группы  , содержащаяся в
, содержащаяся в  , то
, то  метанильпотентна.
метанильпотентна.
Пусть  -
-  -группа и
-группа и  - силовская
- силовская  -подгруппа в
-подгруппа в  . Тогда
. Тогда 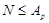 и поэтому по лемме каждая силовская подгруппа из
и поэтому по лемме каждая силовская подгруппа из 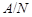 слабо нормальна в
слабо нормальна в  . Поскольку по лемме,
. Поскольку по лемме, 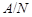
 -квазинормальна в
-квазинормальна в  ,
,


то условия теоремы справедливы для  . Так как
. Так как  , то ввиду выбора группы
, то ввиду выбора группы  ,
,  метанильпотентна.
метанильпотентна.
(4) Условия теоремы справедливы для  (это проямо следует из леммы).
(это проямо следует из леммы).
(5)  разрешима.
разрешима.
Если  , то
, то  метанильпотентна по (4)и выбору группы
метанильпотентна по (4)и выбору группы  . Пусть теперь
. Пусть теперь  . Предположим, что для некоторой силовской подгруппы
. Предположим, что для некоторой силовской подгруппы  из
из  мы имеем
мы имеем  . Тогда ввиду (3),
. Тогда ввиду (3),  разрешима. Пусть теперь
разрешима. Пусть теперь  для каждой силовской подгруппы
для каждой силовской подгруппы  группы
группы  . Тогда по условию каждая силовская подгруппа из
. Тогда по условию каждая силовская подгруппа из  имеет квазинормальной дополнение в
имеет квазинормальной дополнение в  и поэтому
и поэтому  нильпотентна. Полученное противоречие в выбором группы
нильпотентна. Полученное противоречие в выбором группы  доказывает (5).
доказывает (5).
(6) В группе  имеется в точности одна минимальная нормальная подгруппа
имеется в точности одна минимальная нормальная подгруппа  , содержащаяся в
, содержащаяся в  .
.
Пусть  - минимальная нормальная подгруппа группы
- минимальная нормальная подгруппа группы  , содержащаяся в
, содержащаяся в 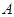 . Тогда
. Тогда  абелева согласно (5), и поэтому ввиду (3),
абелева согласно (5), и поэтому ввиду (3),  метанильпотентна. Так как класс всех метанильпотентных групп. Кроме того, так как класс всех метанильпотентных групп является насыщенной формацией (см.), то
метанильпотентна. Так как класс всех метанильпотентных групп. Кроме того, так как класс всех метанильпотентных групп является насыщенной формацией (см.), то  - единственная минимальная нормальная подгруппа группы
- единственная минимальная нормальная подгруппа группы  , содержащаяся в
, содержащаяся в 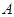 .
.
(7) Если 
 -группа, то каждая силовская
-группа, то каждая силовская  -подгруппа из
-подгруппа из 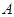 , где
, где  , имеет квазинормальное дополнение в
, имеет квазинормальное дополнение в  .
.
Пусть  - силовская
- силовская  -подгруппа в
-подгруппа в  , где
, где  . Тогда ввиду (6),
. Тогда ввиду (6),  . По условию,
. По условию,  слабо нормальна в
слабо нормальна в  и поэтому
и поэтому  имеет квазинормальную подгруппу
имеет квазинормальную подгруппу  , такую что
, такую что  и
и

Заключительное противоречие.
Пусть  - силовская
- силовская  -подгруппа в
-подгруппа в  и
и  . Тогда
. Тогда

По условию  имеет квазинормальную подгруппу
имеет квазинормальную подгруппу  , такую что
, такую что  и
и

Тогда


и поэтому 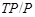 - дополнение для
- дополнение для  в
в 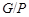 , которое является квазинормальной в
, которое является квазинормальной в 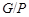 подгруппой. Если
подгруппой. Если  -
-  -подгруппа из
-подгруппа из 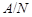 , где
, где  , то ввиду (7),
, то ввиду (7),  имеет дополнение в
имеет дополнение в 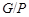 , которое является квазинормальной подгруппой (см. доказательство утверждения (3) леммы). Тогда по лемме,
, которое является квазинормальной подгруппой (см. доказательство утверждения (3) леммы). Тогда по лемме, 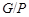 нильпотентна и поэтому
нильпотентна и поэтому  метанильпотентна. Полученное противоречие доказывает метанильпотентность группы
метанильпотентна. Полученное противоречие доказывает метанильпотентность группы  .
.
Обратно, предположим, что  метанильпотентна. Покажем, что каждая силовская подгруппа из
метанильпотентна. Покажем, что каждая силовская подгруппа из  слабо нормальна в
слабо нормальна в  . Предположим, что это не верно и пусть
. Предположим, что это не верно и пусть  - контрпример минимального порядка. Тогда
- контрпример минимального порядка. Тогда  имеет силовскую подгруппу
имеет силовскую подгруппу  , которая не является слабо нормальной в
, которая не является слабо нормальной в  . Пусть
. Пусть  - произвольная минимальная нормальная подгруппа в
- произвольная минимальная нормальная подгруппа в  и
и 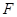 - подгруппа Фиттинга группы
- подгруппа Фиттинга группы  . Предположим, что
. Предположим, что  . Тогда
. Тогда  слабо нормальна в
слабо нормальна в  и поэтому по лемме (1),
и поэтому по лемме (1), 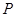 слабо нормальна в
слабо нормальна в  , противоречие. Значит,
, противоречие. Значит,  и поэтому
и поэтому

Так как по условию  метанильпотентна и
метанильпотентна и  - силовская подгруппа в
- силовская подгруппа в  , то
, то  имеет нормальное дополнение
имеет нормальное дополнение  в
в  . Но поскольку
. Но поскольку  и
и  -
-  -группы, то
-группы, то  - нормальное дополнение для
- нормальное дополнение для  в
в  . Следовательно,
. Следовательно,  слабо нормальна в
слабо нормальна в  . Полученное противоречие показывает, что каждая силовская подгруппа из
. Полученное противоречие показывает, что каждая силовская подгруппа из  слабо нормальна в
слабо нормальна в  .
.
Пусть  - группа тогда следующие утверждения эквивалентны:
- группа тогда следующие утверждения эквивалентны:
(1)  - метанильпотентна;
- метанильпотентна;
(2)  , где подгруппа
, где подгруппа  субнормальна в
субнормальна в  ,
,  - абелева холлова подгруппа в
- абелева холлова подгруппа в  и каждая силовская подгруппа из
и каждая силовская подгруппа из  слабо квазинормальна в
слабо квазинормальна в  ;
;
(3)  , где подгруппа
, где подгруппа 
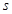 -квазинормальна в
-квазинормальна в  ,
,  - нильпотентна и каждая силовская подгруппа из
- нильпотентна и каждая силовская подгруппа из  слабо нормальна в
слабо нормальна в  .
.
Пусть  , где подгруппа
, где подгруппа 
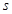 -квазинормальна в
-квазинормальна в  ,
,  нильпотентна. Предположим, что любая максимальная подгруппа каждой нециклической подгруппы из
нильпотентна. Предположим, что любая максимальная подгруппа каждой нециклической подгруппы из  слабо нормальна в
слабо нормальна в  . Тогда
. Тогда  сверхразрешима.
сверхразрешима.
Доказательство. Предположим, что эта теорема не верна и пусть  - контрпример минимального порядка. Тогда:
- контрпример минимального порядка. Тогда:
(1) Каждая собственная подгруппа  группы
группы  , содержащая
, содержащая  , сверхразрешима.
, сверхразрешима.
Пусть  , где
, где  . Тогда
. Тогда

где  нильпотентна и
нильпотентна и 
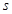 -квазинормальна в
-квазинормальна в  . Так как по лемме (2), любая максимальная подгруппа каждой нециклической силовской подгруппы из
. Так как по лемме (2), любая максимальная подгруппа каждой нециклической силовской подгруппы из  слабо нормальна в
слабо нормальна в  и
и  , то по выбору группы
, то по выбору группы  мы имеем (1).
мы имеем (1).
(2) Пусть 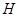 - неединичная нормальная подгруппа в
- неединичная нормальная подгруппа в  . Предположим, что
. Предположим, что 
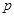 -группа. Допустим, что
-группа. Допустим, что 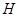 содержит силовскую
содержит силовскую  -подгруппу
-подгруппу  из
из  , или
, или 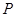 циклична, или
циклична, или  . Тогда
. Тогда  сверхразрешима.
сверхразрешима.
Если  , то
, то

нильпотентна. Пусть теперь  . Так как
. Так как  , то нам только нужно показать, что условия теоремы справедливы для
, то нам только нужно показать, что условия теоремы справедливы для  . Ясно, что
. Ясно, что
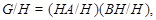
где 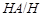
 -квазинормальна в
-квазинормальна в  и
и  нильпотентна. Пусть
нильпотентна. Пусть  силовская
силовская  -подгруппа из
-подгруппа из  и
и  - произвольная максимальная подгруппа в
- произвольная максимальная подгруппа в  . Пусть
. Пусть  - силовская
- силовская  -подгруппа из
-подгруппа из  , такая что
, такая что  . Ясно, что
. Ясно, что  - силовская
- силовская  -подгруппа группы
-подгруппа группы  . Значит,
. Значит, 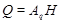 для некоторой силовской
для некоторой силовской  -подгруппы
-подгруппы 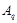 из
из  . Предположим, что
. Предположим, что  не является циклической подгруппой. Тогда
не является циклической подгруппой. Тогда 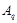 не циклична. Покажем, что
не циклична. Покажем, что  слабо нормальна в
слабо нормальна в  . Если
. Если  , то это прямо следует из леммы. Допустим, что либо силовская
, то это прямо следует из леммы. Допустим, что либо силовская  -подгруппа
-подгруппа  из
из  циклическая, либо
циклическая, либо  . Тогда
. Тогда  . Покажем, что
. Покажем, что  - максимальная в
- максимальная в 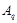 подгруппа. Так как
подгруппа. Так как  и
и  , то
, то
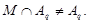
Предположим, что для некоторой подгруппы  из
из  мы имеем
мы имеем

где
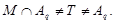
Тогда

Так как  - максимальная в
- максимальная в  подгруппа, то либо
подгруппа, то либо  , либо
, либо  . Если
. Если  , то
, то

что противоречит выбору подгруппы  . Значит,
. Значит,  и поэтому мы имеем
и поэтому мы имеем

противоречие. Следовательно,  - максимальная в
- максимальная в 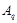 подгруппа и по условию
подгруппа и по условию  слабо нормальна в
слабо нормальна в  . Значит,
. Значит,

слабо нормальна в  . Следовательно, условия теоремы справедливы для
. Следовательно, условия теоремы справедливы для  .
.
(3)  и
и  сверхразрешима.
сверхразрешима.
По выбору группы  ,
,  и поэтому
и поэтому  сверхразрешима согласно (1).
сверхразрешима согласно (1).
(4)  - разрешимая группа.
- разрешимая группа.
По условию 
 -квазинормальна в
-квазинормальна в  и поэтому по лемме (3),
и поэтому по лемме (3),  содержится в некоторой разрешимой нормальной подгруппе
содержится в некоторой разрешимой нормальной подгруппе  группы
группы  . Так как группа
. Так как группа  нильпотентна, то
нильпотентна, то  разрешима.
разрешима.
(5) Если  - простое число и
- простое число и  , то
, то  .
.
Пусть  . Тогда ввиду (2),
. Тогда ввиду (2),  сверхразрешима. Если
сверхразрешима. Если  - множество всех простых делителей порядка группы
- множество всех простых делителей порядка группы  , то по лемме (1),
, то по лемме (1),  , где
, где 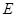 - нормальная
- нормальная  -подгруппа группы
-подгруппа группы  и поэтому
и поэтому

сверхразрешима. Но тогда

сверхразрешима. Полученное противоречие с выбором группы  доказывает (5).
доказывает (5).
(6)  .
.
Допустим, что 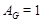 . Тогда по лемме,
. Тогда по лемме,  нильпотентна. Пусть
нильпотентна. Пусть 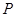 - силовская
- силовская  -подгруппа из
-подгруппа из  . Так как ввиду леммы (3)
. Так как ввиду леммы (3)  субнормальна в
субнормальна в  , то
, то 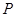 субнормальна в
субнормальна в 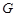 . Тогда
. Тогда  , согласно лемме (1). Но тогда ввиду (2),
, согласно лемме (1). Но тогда ввиду (2),  сверхразершима и поэтому
сверхразершима и поэтому  , по выбору группы
, по выбору группы  . Так как
. Так как  и
и

нильпотентно, то  - силовская
- силовская  -подгруппа из
-подгруппа из  . Пусть
. Пусть  - холлова
- холлова  -подгруппа из
-подгруппа из  и
и  . По лемме,
. По лемме,  нормальна в
нормальна в  и поэтому
и поэтому  . Допустим, что для некоторого простого делителя порядка
. Допустим, что для некоторого простого делителя порядка  , отличного от
, отличного от 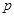 , мы имеем
, мы имеем  . Тогда
. Тогда  нормальна в
нормальна в  и поэтому
и поэтому  - нормальная подгруппа в
- нормальная подгруппа в  , поскольку
, поскольку  . Но тогда
. Но тогда 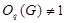 , что противоречит (5). Следовательно,
, что противоречит (5). Следовательно,  и поэтому
и поэтому  . Согласно теореме,
. Согласно теореме,  сверхразрешима и поэтому
сверхразрешима и поэтому  - абелева группа, экспонента которой делит
- абелева группа, экспонента которой делит  , согласно леммы. Но тогда
, согласно леммы. Но тогда  - абелева группа экспоненты, делящей
- абелева группа экспоненты, делящей  и поэтому
и поэтому  сверхразрешима, согласно леммы. Полученное противоречие с выбором группы
сверхразрешима, согласно леммы. Полученное противоречие с выбором группы  доказывает (6).
доказывает (6).
Заключительное противоречие.
Пусть  - минимальная нормальная подгруппа в
- минимальная нормальная подгруппа в  , содержащаяся в
, содержащаяся в  . Пусть
. Пусть  -
-  -группа и
-группа и  - силовская
- силовская  -подгруппа группы
-подгруппа группы  . В силу (2),
. В силу (2),  сверхразрешима и поэтому
сверхразрешима и поэтому  - единственная минимальная нормальная подгруппа группы
- единственная минимальная нормальная подгруппа группы 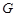 , содержащаяся в
, содержащаяся в  . Ясно, что
. Ясно, что 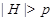 и
и  . Значит, по лемме для некоторой максимальной подгруппы
. Значит, по лемме для некоторой максимальной подгруппы  из
из  мы имеем
мы имеем  . Ясно, что
. Ясно, что  и поэтому по условию
и поэтому по условию  имеет дополнение
имеет дополнение  в
в 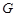 , которое является квазинормальной в
, которое является квазинормальной в  подгруппой. Тогда
подгруппой. Тогда

и поэтому  . Но тогда
. Но тогда

и поэтому, ввиду минимальности  ,
,  . Ввиду (5),
. Ввиду (5),  имеет холлову
имеет холлову  -подгруппу. Так как в силу леммы (3),
-подгруппу. Так как в силу леммы (3),  субнормальна в
субнормальна в  , то каждая холлова
, то каждая холлова  -подгруппа группы
-подгруппа группы  содержится в
содержится в  . Следовательно,
. Следовательно,  -
-  -группа. Отсюда следует, что
-группа. Отсюда следует, что

сверхразрешима. Полученное противоречие завершает доказательство теоремы.
Группа 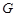 дисперсивна по Оре тогда и только тогда, когда
дисперсивна по Оре тогда и только тогда, когда  , где подгруппа
, где подгруппа  квазинормальна в
квазинормальна в  ,
, 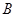 дисперсивна по Оре и каждая максимальная подгруппа любой нециклической силовской подгруппы группы
дисперсивна по Оре и каждая максимальная подгруппа любой нециклической силовской подгруппы группы  слабо нормальна в
слабо нормальна в  .
.
Доказательство. Пусть  , где подгруппа
, где подгруппа  квазинормальна в
квазинормальна в  ,
,  дисперсивна по Оре и каждая максимальная подгруппа любой нециклической силовской подгруппы группы
дисперсивна по Оре и каждая максимальная подгруппа любой нециклической силовской подгруппы группы  слабо нормальна в
слабо нормальна в  . Покажем, что группа
. Покажем, что группа 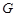 дисперсивна по Оре. Предположим, что это не верно и пусть
дисперсивна по Оре. Предположим, что это не верно и пусть  - контрпример минимального порядка. Тогда:
- контрпример минимального порядка. Тогда:
(1) Каждая собственная подгруппа  группы
группы 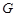 , содержащая
, содержащая  , дисперсивна по Оре.
, дисперсивна по Оре.
Пусть  , где
, где  . Тогда
. Тогда

где  дисперсивна по Оре и
дисперсивна по Оре и  квазинормальна в
квазинормальна в  . Так как по лемме (2) любая максимальная подгруппа каждой нециклической силовской подгруппы из
. Так как по лемме (2) любая максимальная подгруппа каждой нециклической силовской подгруппы из  слабо нормальна в
слабо нормальна в  и
и  , то по выбору группы
, то по выбору группы  мы имеем (1).
мы имеем (1).
(2) Пусть  - неединичная нормальная подгруппа в
- неединичная нормальная подгруппа в  , являющаяся
, являющаяся  -группа для некоторого простого числа
-группа для некоторого простого числа  . Допустим, что либо
. Допустим, что либо  содержит силовскую
содержит силовскую  -подгруппу
-подгруппу  из
из  , либо
, либо  циклична, либо
циклична, либо  . Тогда
. Тогда 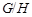 дисперсивна по Оре.
дисперсивна по Оре.
Если  , то
, то

дисперсивна по Оре. Пусть теперь  . Так как
. Так как  , то нам лишь нужно показать, что условия теоремы справедливы для
, то нам лишь нужно показать, что условия теоремы справедливы для 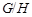 . Ясно, что
. Ясно, что

где  квазинормальна в
квазинормальна в 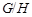 и
и  дисперсивна по Оре. Пусть
дисперсивна по Оре. Пусть  силовская
силовская  -подгруппа из
-подгруппа из  и
и  - произвольная максимальная подгруппа в
- произвольная максимальная подгруппа в  . Пусть
. Пусть  - силовская
- силовская  -подгруппа из
-подгруппа из  , такая что
, такая что  . Ясно, что
. Ясно, что  - силовская
- силовская  -подгруппа группы
-подгруппа группы  . Значит,
. Значит,  для некоторой силовской
для некоторой силовской  -подгруппы
-подгруппы  из
из  . Предположим, что
. Предположим, что  не является циклической подгруппой. Тогда
не является циклической подгруппой. Тогда 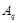 не циклична. Покажем, что
не циклична. Покажем, что  слабо нормальна в
слабо нормальна в 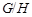 . Если
. Если  , то это прямо следует из леммы. Допустим, что либо силовская
, то это прямо следует из леммы. Допустим, что либо силовская  -подгруппа
-подгруппа  из
из  циклическая, либо
циклическая, либо 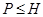 . Тогда
. Тогда  . Покажем, что
. Покажем, что  - максимальная в
- максимальная в  подгруппа. Так как
подгруппа. Так как  и
и  , то
, то

Предположим, что для некоторой подгруппы 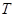 из
из  мы имеем
мы имеем

где

Тогда

Так как  - максимальная в
- максимальная в  подгруппа, то либо
подгруппа, то либо  , либо
, либо  . Если
. Если 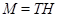 , то
, то  , что противоречит выбору подгруппы
, что противоречит выбору подгруппы 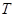 . Значит,
. Значит,  и поэтому мы имеем
и поэтому мы имеем

противоречие. Следовательно, 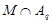 - максимальная в
- максимальная в  подгруппа и по условию
подгруппа и по условию 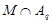 слабо нормальна в
слабо нормальна в  . Значит,
. Значит,
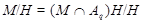
слабо нормальна в 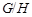 . Следовательно, условия теоремы справедливы для
. Следовательно, условия теоремы справедливы для  .
.
(3) Если  - простое число и
- простое число и  , то
, то  .
.
Пусть

Тогда ввиду (2), 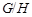 дисперсивна по Оре. С другой стороны, если
дисперсивна по Оре. С другой стороны, если  - множество всех простых делителей
- множество всех простых делителей  , то ввиду леммы (3) и леммы,
, то ввиду леммы (3) и леммы,  , где
, где  - нормальная
- нормальная  -подгруппа в
-подгруппа в