КОНТРОЛЬНАЯ РАБОТА
Вариант№ 72.
ВЫПОЛНИЛ:
Студент группы ПТЗ-30118 / Климко М.Я. /
Подпись Фамилия, И.О.
ПРОВЕРИЛ:
Преподаватель: / Крохмаль Н.Н. /
Подпись Фамилия, И.О.
Курган 2021
Задание 1 структурный анализ двух механических систем
1) обозначить цифрами элементы, т. е. тела (пока не знаем детали или звенья), подвижно соединенные между собой;
2) обозначить латинскими буквами кинематические пары, образуемые этими элементами;
3) определить по формуле Чебышева число W рассматриваемой системы; 4) ответить на вопрос: «Является ли данная система механизмом, статически определимой фермой или статически неопределимой фермой?»
Для механической системы, под номер 7 обозначим цифрами элементы и кинематические пары.
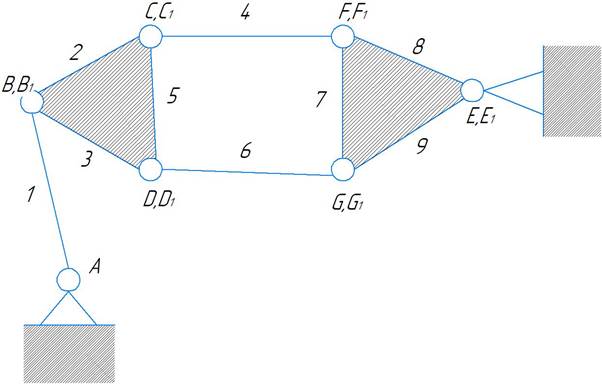
Заметим что детали 2,3,5 и 7,8,9 неподвижны друг относительно друга и образуют единые звенья. С точки зрения теории механизмов более корректно перейти к эквивалентной схеме.
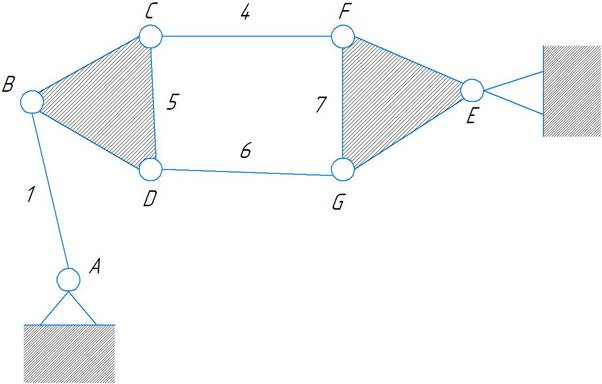
Система содержит 5 подвижных элементов и 7 кинематических вращательных пар 5 класса.
A(0-1), B(1-5), C(5-4), D(5-6), F(4-7), G(6-7),E(0-7).
По формуле Чебышева найдем число степеней свободы W:
W = 3*5 - 2*7 - 0 =1, Следовательно данная система является механизмом.
Для механической системы, под номер 2 обозначим цифрами элементы и кинематические пары.
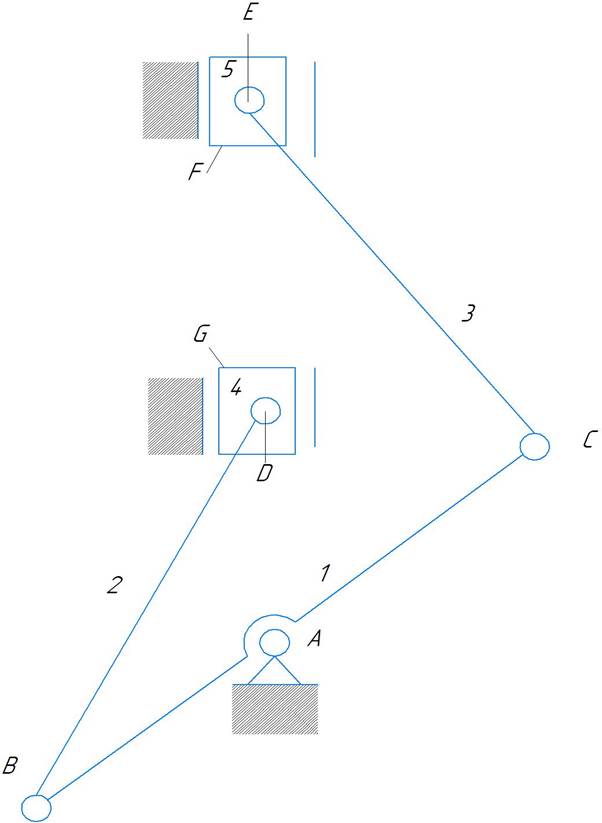
Система содержит 5 подвижных элементов и 7 кинематических (5 вращательных и 2 поступательных) пар 5 класса.
A(0-1 вращательная), B(1-2 вращательная), C(1-3 вращательная),
D(2-4 вращательная), E(3-5 вращательная), F(0-5 поступательная),
G(0-4 поступательная).
По формуле Чебышева найдем число степеней свободы W:
W = 3*5 - 2*7 - 0 =1, Следовательно данная система является механизмом.
Задание 2 кинематический анализ рычажного механизма.
Дано: LAB / L0A =1.7 и e / L0A =0.6
ω1 = 1  ; LOA=0,025 м; LAS=0,5 L постоянные переменные
; LOA=0,025 м; LAS=0,5 L постоянные переменные
1) Вычертим кинематическую схему механизма в 8 совмещенных положениях. Масштаб построения:
µl = LOA / [OA] =0,0017, м/мм,
где LOA – длина звена ОА, м;
[ОА], мм – отрезок, изображающий это звено на схеме.
2) Вычертим шатунную кривую – траекторию точки S, принадлежащей звену 2; 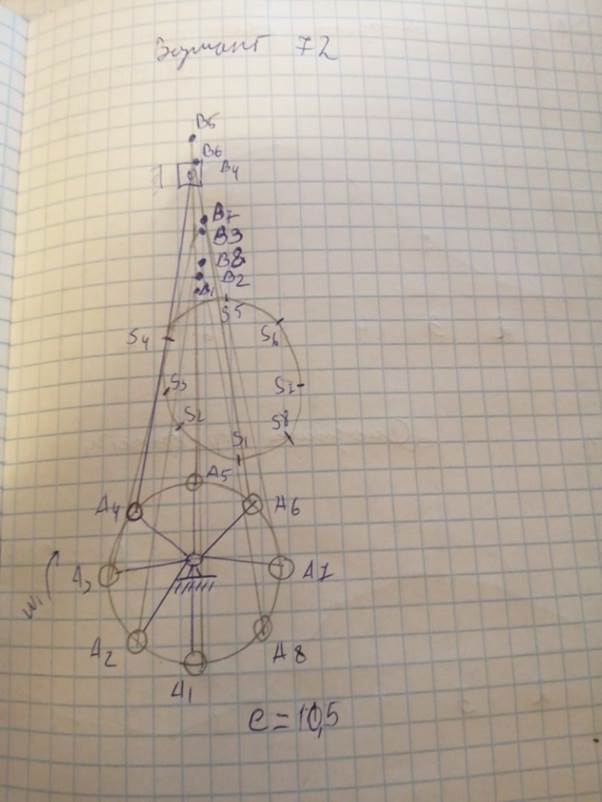
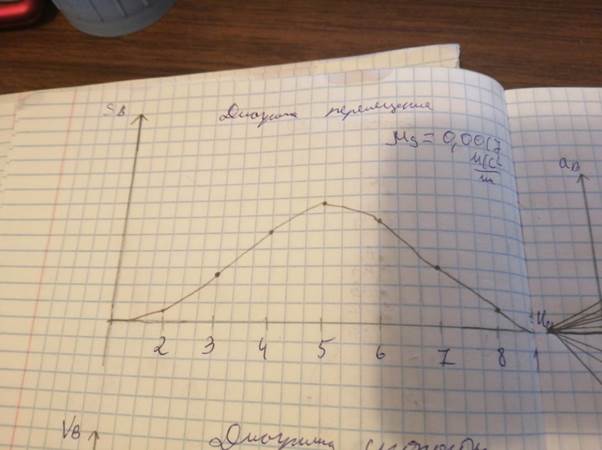
3) Построить диаграмму перемещений точки В, отложив по оси ординат линейное перемещение этой точки, а по оси абсцисс – время одного оборота кривошипа (звена 1). Масштаб по оси ординат µS = µl. =0,0017 м/мм
Масштаб по оси абсцисс:
µt = 2π/ωL, c-1/ мм,
где L – выбирается произвольно;
ω – угловая скорость кривошипа, c-1.
µt = 2π/1 ∙100 = 0,0628 с/мм
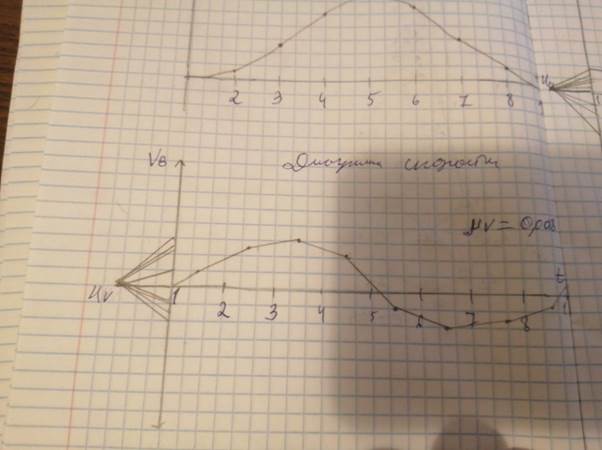
4) Строим диаграмму скоростей точки В способом графического дифференцирования. Для этого на продолжении оси абсцисс диаграммы скоростей, на расстоянии Hv (15 мм) от ее начала выбираем точку Рv. Через эту точку провести прямую параллельную хорде 1-21 (диаграммы перемещений). Пересечение проведенной прямой с осью ординат соответствует значению скорости точки В на середине отрезка 1-2 оси абсцисс диаграммы скоростей. Далее аналогичным образом сносят хорды 21-31, 31-41, 41-51.
Масштаб скорости:
µv = µS/ Hv µt, м c-1 /мм.
µv = 0,0017/(15*0.0628)=0.0018
5) Аналогичным образом строим диаграмму ускорения точки В, дифференцируя по времени диаграмму скоростей. Масштаб ускорения:
µа = µS/ Hv µt, м c-1 /мм.
µа = 0,0017/(15*0.0628)=0.0018
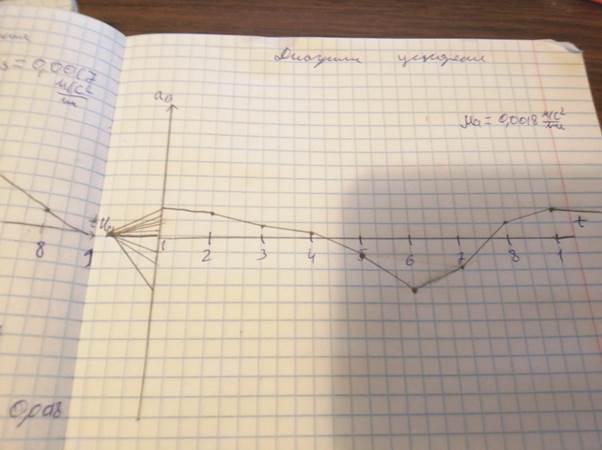
6) Определяем численные значения скорости и ускорения точки В для восьми положений механизма, умножив ординаты точек на диаграммах (в мм) на соответствующий масштаб (µv или µа). Результаты заносим в таблицу 2.
Таблица 2 - Скорости и ускорения точки В.
| VB, м/с | 0,0162 | 0,0252 | 0,0234 | -0,0126 | -.0 0162 | -0,0108 | ||
| aB, м/с2 | 0,0180 | 0,0135 | 0,0072 | -0,0011 | -0,0090 | -0,0270 | -0.0162 | 0,094 |