В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го – 525 шт., с 3-го – 275 шт. и с 4-го – 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го – 0,30, для 3-го – 0,20, для 4-го – 0,10. При раскладке по полкам магазина лампочки были перемешаны.
а) Какова вероятность того, что купленная лампочка прогорит более 1500 часов?
б) Купленная лампочка прогорела более 1500 часов. С какой вероятностью она была изготовлена 1-м заводом?
Для решения этой задачи воспользуемся формулой полной вероятности и формулой Бейеса.
Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий H 1, H 2,..., H n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A.
.
События H 1, H 2,..., H n часто называют «гипотезами».
Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Бейеса
.
а) Пусть A – событие, состоящее в том, что купленная лампочка прогорит более 1500 часов. Лампочка может быть изготовлена любым из четырёх заводов, поэтому возможны 4 гипотезы Н 1 – лампочка изготовлена 1-м заводом, Н 2, Н 3 и Н 4 – изготовлена соответственно 2-м, 3-м или 4-м заводом. Так как всего лампочек 250+525+275+950=2000 шт., то вероятности гипотез соответственно равны:
; 
; 
; 
.
Условная вероятность того, что лампочка, изготовленная 1-м заводом, прогорит более 1500 часов равна 
. Условная вероятность того, что лампочка, изготовленная 2-м заводом, прогорит более 1500 часов равна 
. Аналогично 
и 
(это следует из условия задачи).
Используя формулу полной вероятности, имеем
.
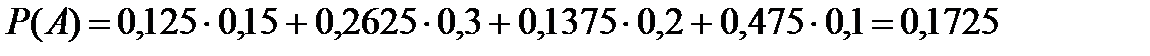б) Так как событие А уже произошло, то искомую вероятность найдём по формуле Бейеса, т.е. переоценим вероятность гипотезы Н 1:
.
Ответ: а) вероятность того, что лампочка прогорит более 1500 часов равна 0,1725;
б) вероятность того, что лампа, прогоревшая 1500 часов, изготовлена 1-м заводом равна 0,11.
Рекомендуемая литература
Основная литература
1. Красс, М.С. Математика для экономистов.- СПб, 2007. РМО
2. Ильин, В.А. Математический анализ: Учеб. в 2-х ч./Под ред. А.Н.Тихонова.- М., 2004. УМО
3. Кудрявцев, Л.Д. Краткий курс математического анализа. В 2-х Т.- М., 2003. РМО
4. Берман, Г.Н. Сборник задач по курсу математического анализа: учеб. пособие.- СПБ, 2008.
5. Беклемишев, Д.В. Курс аналитической геометрии и линейной алгебры: Учеб.-М.: Физматлит, 2004. РМО
6. Ильин, В.А. Линейная алгебра: Учеб.- М., 2004.РМО
7. Красс, М.С. Математика для экономистов: учеб. пособие.- СПб: Питер, 2010. УМО
8. Практикум по высшей математике для экономистов/ Под ред. Н.Ш. Кремера: учеб.-М.: Юнити, 2005.
9. Гмурман, В.Е. Теория вероятностей и математическая статист. М., 2010. РМО
Гмурман, В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие.-М. Высш. образование, 2009. РМО
Дополнительная литература
1. Высшая математика для экономистов: Учеб.-/Н. Ш. Кремер.-М., 2010. УМО
2. Ильин, В.А. Высшая математика: Учеб.- М., 2009. РМО
3. Письменный, Т.Д. Конспект лекций по высшей математике.- М., 2007
4. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2-х ч. – М.,2009. Ч.1-2.
5. Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах: Учеб. пособие / Под ред. В. Ф. Бутузова. — 2-е изд., испр. — М.: ФИЗМАТЛИТ, 2002. — 248 с.
6. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. Учебник. В 2-х частях. - М.: Финансы и статистика, 2006. - 384с.
7. Умнов А.Е. Аналитическая геометрия и линейная алгебра. Учеб. пособие. - М.: МФТИ, 2009 - 570 с.
8. Кремер, Н.Ш.Теория вероятностей и математическая статистика.- М.,2009. РМО
9. Колемаев, В.А. Теория вероятностей и математическая статистика:Учеб.- М.: Кнорус, 2009. УМО
10. Письменный, Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам.-М., 2008