При технологическом проектировании встречаются задачи, число решений которых невелико, а логические зависимости их выбора сложны. В этом случае могут быть использованы алгоритмические таблицы решений.
Пример. Выбор модели токарного автомата.
Таблица 12.1
Комплекс условий применимости (КУП) для выбора станка:
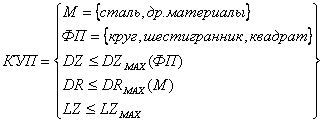
В КУП приняты следующие обозначения: М – материал обрабатываемой заготовки (детали); ФП – форма прутка, применяемого в качество заготовки.
Для решения поставленной задачи можно использовать таблицу решений. Но она будет громоздкой, т.к. условия применимости здесь взаимосвязаны, и объем таблицы решений будет в данном примере в 6 раз больше, чем таблица исходных характеристик станков. Уменьшение объемов таблицы и исключения повторов информации при сложной логике достигают при использовании алгоритмических таблиц решений.
Таблица 12.2
| Алгоритмическая таблица решений для выбора модели токарного автомата | ||||||
| No строки | ФП (1) | DZ (2) | M (3) | DR (4) | LZ (5) | Решение  (6)
|
| =0(4.1) | 
| =0(4.4) | 
| 
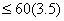
| 1Б112 | |
| =0(4.1) | 
| =0(5.4) | 
|
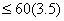
| 1Б118 | |
| =0(4.1) | 
| =0(6.4) |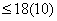 
| 
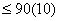
| 1А124 | |
| =6(7.1) | 
| =1(1.4) |
| 
| 1Б112 | |
| =6(7.1) |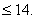 
| =1(2.4) | 
|
| 1Б118 | |
| =6(7.1) | 
| =1(3.4) |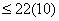 
|
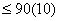
| 1А124 | |
| =4(10) |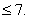 
| =0(4.4) |
| 
| 1Б112 | |
| =4(10) |
| =0(5.4) |
|
| 1Б118 | |
| =4(10) |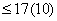 
| =0(6.4) |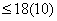
|
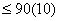
| 1А124 |
В таблице приняты следующие обозначения по ФП: 0 – круглый, 4 – четырехгранный, 6 – шестигранный; по М: 0 – сталь, 1 – другие материалы. Числом «10» условно обозначен номер следующей подпрограммы, к которой осуществляется переход после решении задачи по выбору модели станка.
Каждый элемент таблицы записывается следующим образом: 
, где 
- тип условия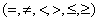 
; 
- характеристическое значение параметра применимости;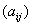 
- адрес (метка) перехода. Имеется три вида переходов:
1. Стандартный – к следующей строке таблицы 
данного столбца 
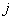(обозначается точкой).
2. Переход к строке 
и столбцу 
данной таблицы, где - номер строки (целая часть 
); - номер столбца (дробная часть ).
3. Переход к другой подпрограмме, при этом - целое число (номер подпрограммы).
Пример поиска. Выбрать токарный автомат на операцию обработки детали из шестигранного стального прутка с размером под ключ 14 мм, у детали имеется резьба М10, длина детали равна 40 мм.
Множество исходных данных запишется следующим образом: U = {ФП, DZ, M, DR, LZ} = {6, 14, 0, 10, 40}. Обозначим через элемент таблицы. Тогда схема поиска:
.
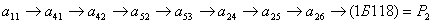Таблицы (матрицы) соответствий
Таблицы решений используют, когда необходимо найти одно решение. Если же нужно найти все допустимые решения, то применяют таблицы соответствий.
Пример. Выбор возможных моделей зубошевинговальных станков (см. ранее). Таблица соответствий представлена в табл. 12.3.
Таблица 12.3
В левой части таблицы соответствий – множество решений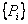 
. В верхней части таблицы – комплекс параметров применимости и их значения. Центральная часть таблицы – матрица соответствий, в которой зафиксированы связи между решениями и значениями параметров, определяющими их применимость: 1 – наличие связи; 0 – отсутствие связи.
Пусть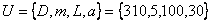 
. Задача решается нахождением соответствующих столбцов (для примера они выделены) и логическим умножением их содержимого. Если результатом логического умножения является «единица», то решение принимается, если «нуль», то не принимается. Для нашего примера возможными (допустимыми) решениями являются: 
и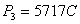 
.
Логические таблицы (матрицы) соответствий
Таблицы решений применяют тогда, когда параметры применимости взаимно независимы. Но условия выбора решений могут быть сложнее.
Пример. Выбор абразивного материала шлифовального круга.
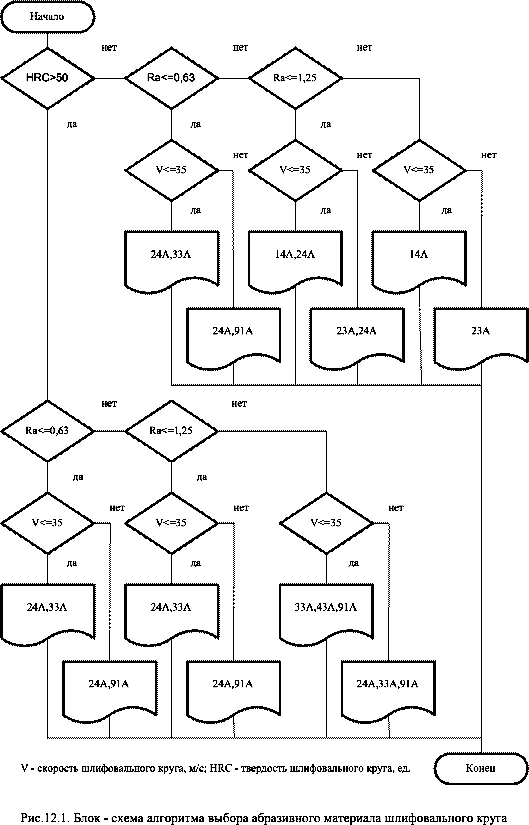
Блок – схема алгоритма выбора абразивного материала шлифовального круга представлена на рис.12.1.
Пусть Ra > 1,25 мкм, V <= 35 м/с. При HRC <= 50 ед. решением будет абразивный материал марки 14А, при HRC > 50 ед. решением будет абразивные материалы марок 33А, 43А, 91А. Пусть теперь Ra > 1,25 мкм, V > 35 м/с. При HRC <= 50 ед. решением будет абразивный материал марки 23А, при HRC >50 ед. решением будет абразивные материалы марок 24А, 33А, 91А.
Если здесь применить таблицу соответствий, то часть решений либо «пропадет», либо будет неверной. При выборе возможных (допустимых) моделей зубошевинговальных станков с помощью таблиц соответствий параметры применимости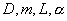 
были независимыми. Здесь же параметры (условия) Ra, V, HRC являются зависимыми, и выбор решений зависит не только от их значений, но и от их сочетаний.
Построим логическую таблицу соответствий для рассматриваемого примера – см. табл. 12.4.
Таблица 12.4
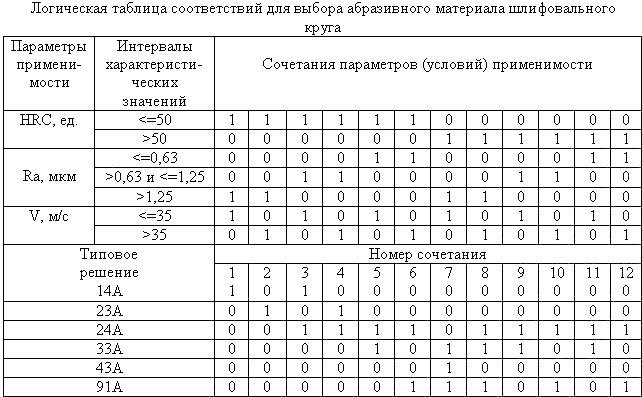
В логическую таблицу соответствий заложены две матрицы:
1. Матрица условий – верхняя правая часть.
2. Матрица решений – нижняя правая часть.
Элементами этих матриц являются булевые переменные, принимающие два значения: 1 – да, 0 – нет.
По матрице условий определяют нужный столбец, для которого в матрице решений выбирают все допустимые решения. Например, HRC <=50 ед.; 0,63 < Ra <= 1,25; V > 35 м/с. Этим исходным данным соответствует 4 столбец, решения – 23А, 24А.
ЛЕКЦИЯ 13