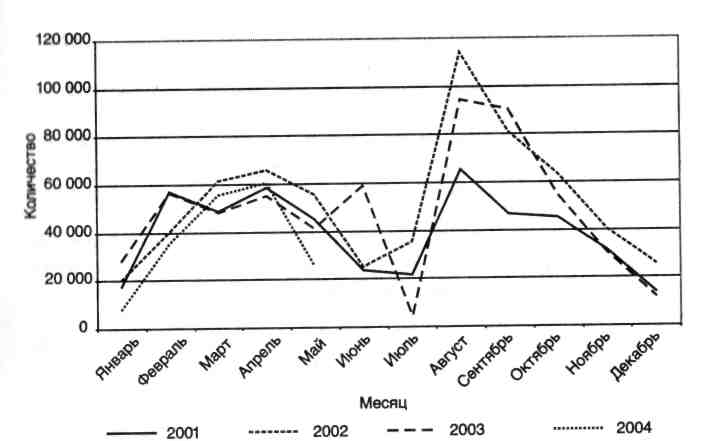
|
Глядя на рис. 8 и 9, можно предположить, что динамика поступлений тесно связана с отгрузками. Для точного вывода требуется провести более детальный анализ.
Рис. 9. Динамика отгрузок товара со склада в 2001-2004 гг.
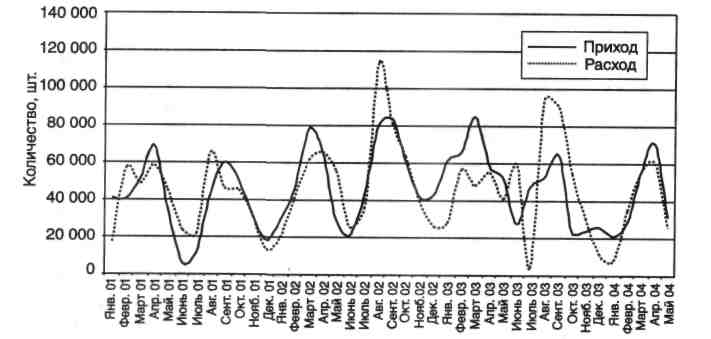
На рис. 10 представлена динамика прихода (сплошные линии) и отгрузок (потребности, объема продаж или товарооборота) (штриховые линии) товара. Тенденции прихода и отгрузок в целом совпадают. Периодически возникающие превышения прихода над отгрузками являются основой повышенного роста отгрузок в дальнейшем периоде. При этом приход имеет более сглаженную динамику, чем отгрузки, что является положительной чертой практики управления запасами товара на складе. В работе с запасом потребление является обслуживаемым фактором, а поставки — организуемым. Более гладкий характер динамики поставок указывает на большую регулярность поставок по сравнению с потреблением.
|
Рис. 10. Динамика прихода и расхода товара в 2001-2004 гг.
Средние показатели входящего и выходящего со склада материальных потоков позволяют получить более обобщенную характеристику соответствия пополнения и использования запаса. Средние показатели пополнения и отгрузок запаса рассчитываются по следующей формуле:
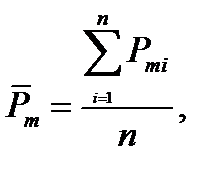(1)
где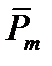 
- среднемесячный объем пополнения (отгрузок, продаж, товарооборота) запаса, единиц/месяц; 
- индекс года статистического ряда; 
- число лет статистических рядов;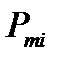 
- объем пополнения (отгрузок, продаж, товарооборота) запаса в месяце 
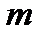года , единиц/месяц.
Средние показатели прихода и отгрузок в примере 1 (рис. 8—10) показывают (рис. 11), что в целом колебания отгрузок значительны, пополнение запаса менее подвержено резким колебаниям. В летний и осенний периоды пополнение запаса медленнее реагирует на изменение отгрузок, чем в зимний и весенний периоды.
|
|
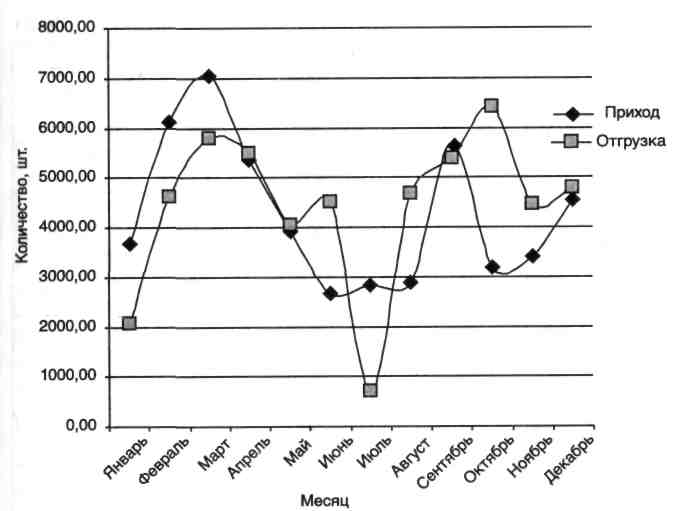
Рис. 11. Динамика средних показателей пополнения и отгрузок запаса за 2001-2004 гг.
Динамика средних показателей прихода и отгрузок (потребности, объема продаж или товарооборота) товара со склада связана с динамикой вариации значений прихода и отгрузок. Вариация показывает степень изменчивости статистического ряда. Она рассчитывается как отношение стандартного отклонения к средней арифметической величине статистического ряда:
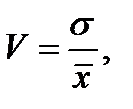(2)
где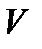 
- коэффициент вариации, доли; 
- стандартное отклонение, единиц; 
- средняя арифметическая величина, единиц.
В свою очередь, стандартное отклонение (или корень из дисперсии) равно
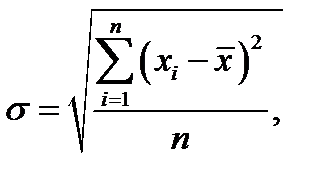(3)
где - стандартное отклонение, единиц; - индекс даты; - число статистических данных; 
- статистическая величина, единиц; - средняя арифметическая величина, единиц, рассчитываемая по формуле:
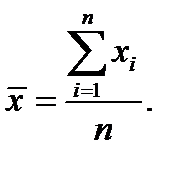(4)
В табл. 1 представлен расчет показателя вариации статистических рядов пополнения и расхода запаса товара на складе из примера 1. За год информация о пополнении запаса представлена в табл. 2, о расходе — в табл. 3. На рис. 12 показана динамика вариации поставок и отгрузок запаса товара.
Таблица 1