Алгоритм решения СЛАУ методом Гаусса

Лабораторная работа №1. Решение системы линейных алгебраических уравнений методом Гаусса

Наиболее распространенным методом решения систем линейных алгебраических уравнений (СЛАУ) является метод Гаусса.

Метод Гаусса для решения СЛАУ обладает рядом преимуществ по сравнению с другими методами:

1) нет необходимости предварительно исследовать систему уравнений на совместность;

2) методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;

3) метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.

Алгоритм решения СЛАУ методом Гаусса

Пусть задана система из линейных уравнений с неиз­вестными:

(1.1)

Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.

На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна.

На втором этапе осуществляется так называемый обратный ход. Суть его заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить систему решений. Если все переменные являются базисными, то единственное решение системы линейных уравнений выражается в численном виде.

Прямой ход. Допустим, что в системе (1.1) коэффициент при в первом уравнении Разделив обе части этого уравнения на , так называемый ведущий элемент, получим равносильную данной систему:

(1.2)

где

Исключим с помощью первого уравнения системы (1.2) неизвестное из всех оставшихся уравнений этой системы. Для этого умножим первое уравнение этой системы последо­вательно на и в том же порядке вычтем получен­ные из второго, третьего и последующих уравнений системы (1.2). В результате получим равносильную систему вида

(1.3)

где

Таким образом, на первом шаге метода Гаусса переменная исключена из всех уравнений, начиная со второго.

Допустим, что коэффициент при во втором урав­нении системы (1.3) отличен от нуля. В противном случае переставим местами уравнения этой системы, записав вторым другое уравнение с подходящим вторым коэффициентом.

На втором шаге будем считать, что ведущий элемент . Исключим неизвестное с помощью второго уравнения из всех последующих уравнений. Для этого разделим второе уравнение на . Затем умножим последовательно полу­ченное второе уравнение на и вычтем эти ре­зультаты из третьего, четвертого и всех оставшихся уравнений.

В итоге получим очередную систему уравнений:

где

Продолжая этот процесс исключения неизвестных, полу­чим либо несовместную, либо совместную систему уравнений. В первом случае в системе будет содержаться уравнение, в ко­тором все коэффициенты левой части равны нулю, а свобод­ный член отличен от нуля, т.е. уравнение вида , где . Во втором случае получим либо систему треугольной формы

(1.4)

либо систему трапециевидной (ступенчатой) формы (раздел 1.2)

(1.5)

Обратный ход. В случае треугольной системы из последнего уравнения (1.4) следует, что 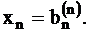Подставляя это значение в пред­последнее уравнение системы (1.4), найдем неизвестное . Подставляя значения и в предыдущее уравнение, найдем значение неизвестного и т.д.

Таким образам, если данная система (1.1) с помощью эле­ментарных преобразований приводится к системе треугольной формы, то система имеет единственное решение (т.е. система совместна и определенна).

ПРИМЕР 1.1Решить систему уравнений методом Гаусса

Решение. Построим расширенную матрицу системы

	Исключаяс помощью первой строки неизвестное из оставшихся строк, получим:
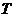~	Исключая неизвестное с помощью второй строки из последующих строк, получим:
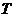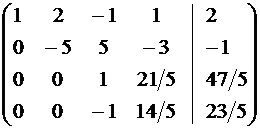
~	Исключаяс помощью третьей строки неизвестное из четвертой строки, получим:
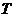~	Матрица, а, следовательно, и система уравнений, приведена к треугольному виду.

Так как матрица системы треугольная, то все переменные – базисные, и система имеет единственное решение.

Проверка Ответ .