Системы уравнений, основная матрица которых прямоугольная или квадратная вырожденная, могут не иметь решений, могут иметь единственное решение, а могут иметь бесконечное множество решений.
Метод Гаусса позволяет установить совместность или несовместность системы линейных уравнений, а в случае ее совместности определить все решения (или одно единственное решение). В принципе процесс исключения неизвестных переменных в случае таких СЛАУ остается таким же. Остановимся подробно на некоторых ситуациях, которые могут возникнуть.
1.2.1 На определенном этапе исключения неизвестных переменных некоторые уравнения системы могут обратиться в тождества 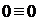 . Это говорит о том, что такие уравнения излишни, то есть, их можно убрать из системы уравнений и продолжить прямой ход метода Гаусса.
. Это говорит о том, что такие уравнения излишни, то есть, их можно убрать из системы уравнений и продолжить прямой ход метода Гаусса.
В этом случае система имеет ступенчатую форму (трапециевидную) (1.5). Тогда, перенося все слагаемые, содержащие неизвестные 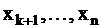 в правую часть уравнений, получим систему вида
в правую часть уравнений, получим систему вида
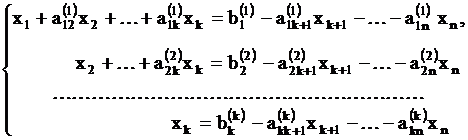 (1.6)
(1.6)
Из (1.6) следует, что значения неизвестных 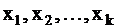 выражаются через значения неизвестных
выражаются через значения неизвестных 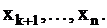 Так как последним неизвестным, называемым свободными неизвестными, можно придавать любые произвольные значения, то система (1.6), а вместе с ней и данная система (1.1), имеет бесконечное множество решений.
Так как последним неизвестным, называемым свободными неизвестными, можно придавать любые произвольные значения, то система (1.6), а вместе с ней и данная система (1.1), имеет бесконечное множество решений.
Итак, если данная система приводится к трапециевидной форме, то она имеет бесконечное множество решений (т.е. система совместна и неопределенна). Найденные решения называются общими решениями системы и записываются в форме
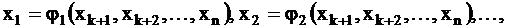
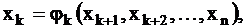
где 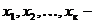 базисные переменные;
базисные переменные; 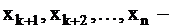 небазисные (свободные) переменные - любые числа. Решения, полученные из общих решений при конкретных значениях свободных неизвестных
небазисные (свободные) переменные - любые числа. Решения, полученные из общих решений при конкретных значениях свободных неизвестных 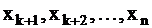 , (небазисных переменных) называются частными решениями.
, (небазисных переменных) называются частными решениями.
ПРИМЕР 1.2 Решить систему уравнений методом Гаусса 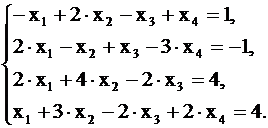
Решение. Составим расширенную матрицу данной системы и выполняя элементарные преобразования над ней, получим
 ~
~  ~
~
~ 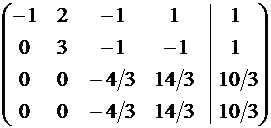 ~
~ 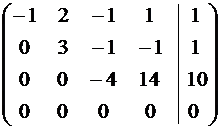 ~
~
Следовательно, четвертое уравнение можно удалить из системы и продолжить решение
~ 
Матрица 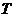 приведена к трапециевидной форме.
приведена к трапециевидной форме.
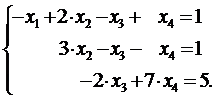
| Тогда  , , 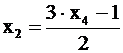 , ,
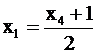 . .
|
Здесь 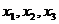 - базисные переменные. Следовательно, общее решение системы запишется в виде
- базисные переменные. Следовательно, общее решение системы запишется в виде
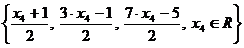 ,
,
где  - небазисная переменная, произвольное число.
- небазисная переменная, произвольное число.
Полагая, например, 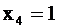 , найдем одно из частных решений
, найдем одно из частных решений 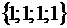 .
.
Замечание.
Расчеты вручную по методу Гаусса значительно упростятся, если коэффициенты при неизвестных будут целыми числами. Для этого нужно, чтобы ведущие элементы были равны единице ( ). Этого можно добиться, совершая элементарные преобразования над строками расширенной матрицы.
). Этого можно добиться, совершая элементарные преобразования над строками расширенной матрицы.
ПРИМЕР 1.3 Решить систему уравнений методом Гаусса 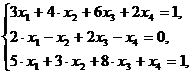
Решение. Составим расширенную матрицу данной системы и выполняя элементарные преобразования над ней (из первого уравнения вычтем второе), получим первый ведущий элемент равный единице
T= 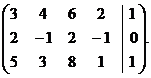 ~
~  ~
~
После первого шага получим
~ 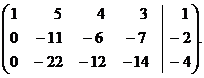 ~
~ 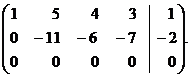 ~
~
~ 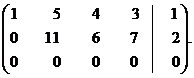
Следовательно, третье уравнение можно удалить из системы.
~ 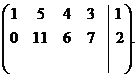
Матрица 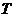 приведена к трапециевидной форме.
приведена к трапециевидной форме.
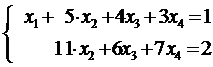 ,
т.е. ,
т.е.
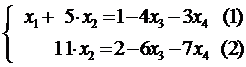
| Тогда из (2), 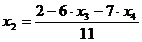 ,
из (1), с учетом (2) ,
из (1), с учетом (2)

|
Переменные  и
и  - небазисные (свободные), а
- небазисные (свободные), а  и
и  - базисные.
- базисные.
Следовательно, общее решение системы запишется в виде
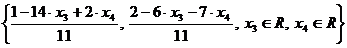 ,
,
где  ,
,  - небазисные переменные, произвольные числа.
- небазисные переменные, произвольные числа.
Полагая, например, 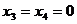 , найдем одно из частных решений
, найдем одно из частных решений 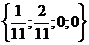 .
.
Можно убедиться, что проверка сходится.
ПРИМЕР 1.4 Методом Гаусса решить систему уравнений  .
.
Решение. Так как ведущий элемент 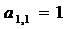 , составляем расширенную матрицу системы и приступаем к первому шагу прямого хода.
, составляем расширенную матрицу системы и приступаем к первому шагу прямого хода.
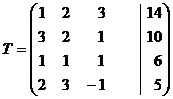 ~
~ 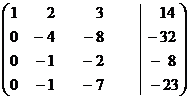 ~
~
Чтобы на втором шаге ведущий элемент был равен единице (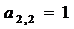 ), третью строку умножаем на -1 и меняем местами строки 2 и 3. Далее приступаем ко второму шагу прямого хода
), третью строку умножаем на -1 и меняем местами строки 2 и 3. Далее приступаем ко второму шагу прямого хода
~  ~
~  ~
~
Третье уравнение можно удалить из системы и после третьего шага, приступить к обратному ходу
~  ~
~ 
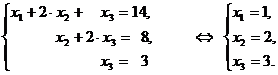
Можно убедиться, что проверка сходится.
1.2.2 При проведении прямого хода метода Гаусса одно (или несколько) уравнений системы могут принять вид 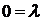 , где
, где 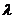 - некоторое число, отличное от нуля. Это говорит о том, что уравнение, которое обратилось в равенство
- некоторое число, отличное от нуля. Это говорит о том, что уравнение, которое обратилось в равенство 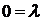 , не может обратиться в тождество ни при каких значениях неизвестных переменных. Другими словами, система линейных алгебраических уравнений в этом случае несовместна (не имеет решения). Наиболее часто такие ситуации встречаются, когда число уравнений в системе больше числа неизвестных переменных.
, не может обратиться в тождество ни при каких значениях неизвестных переменных. Другими словами, система линейных алгебраических уравнений в этом случае несовместна (не имеет решения). Наиболее часто такие ситуации встречаются, когда число уравнений в системе больше числа неизвестных переменных.
ПРИМЕР 1.5 Методом Гаусса решить систему уравнений  .
.
Решение. Преобразуем расширенную матрицу системы
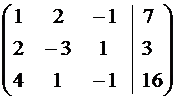 ~
~ 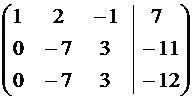 ~
~  .
.
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 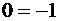 , следовательно, данная система несовместна.
, следовательно, данная система несовместна.
Заключение
Мы рассмотрели решение различных систем линейных алгебраических уравнений методом Гаусса. Можно сделать следующие выводы:
1) Если в конце прямого хода метода Гаусса мы получаем систему, число уравнений в которой совпадает с числом неизвестных переменных, то система совместна и определена, то есть, имеет единственное решение, которое определяется при проведении обратного хода метода Гаусса.
2) Если после завершения прямого хода метода Гаусса в полученной СЛАУ число уравнений меньше числа неизвестных переменных, то система совместна и имеет бесконечное множество решений, которые находятся при обратном ходе метода Гаусса.
3) Если в процессе прямого хода метода Гаусса одно или несколько уравнений принимают вид 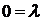 , где
, где 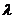 - некоторое число, отличное от нуля, то система несовместна.
- некоторое число, отличное от нуля, то система несовместна.