Вариант 12
Часть 1. Среди множества случайных точек, расположенных в трехмерном пространстве, выбрать подмножество точек, лежащих за пределами эллипсоида заданного размера, имеющего центр, совпадающий с центром тяжести системы координат.
Закон распределения каждой из координат случайных точек – нормальный с одинаковыми средними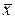 
= 
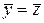и дисперсиями Dx = Dy = Dz.
Обеспечить в графическом окне:
v ввод количества исходных точек,
v параметры распределения
v параметры объемной фигуры в графическом окне.
v построение трехмерного графика, отображающего по выбору пользователя объемную фигуру и/или исходное множество точек и/или найденное подмножество точек контрастным цветом и другим типом.
v отображение точки, являющейся центром тяжести системы координат вторым контрастным цветом и типом.
Предусмотреть возможность изменения исходных параметров и соответствующих им графиков непосредственно в графическом окне.
Часть 2. Среди множества расположенных на плоскости прямых со случайными параметрами выбрать подмножество прямых, расстояние от которых до заданной точки (параметры которой также являются случайными), не превышает пороговой величины R. Обеспечить ввод с клавиатуры количества исходных прямых и величины R в командном окне системы MatLab. Построить график, отображающий исходное множество прямых, и отметить на нем найденное подмножество контрастным цветом. Изобразить на этом же графике точку, расстояние до которой определяется. Предусмотреть возможность изменения исходных параметров и соответствующих им графиков в командном окне Matlab. Закон распределения каждой из координат случайных точек – равномерный с нулевым средним и единичной дисперсией.
|
|
Справочные сведения:
1. Уравнение эллипсоида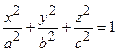 
, где a, b, c – полуоси.
2. Для формирования массива случайных элементов, распределенных по нормальному закону с заданным средним и дисперсией следует умножить данные, полученные с помощью функции randn на величину s и добавить к ним величину 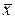, где 
.
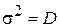3. Для построения объемной фигуры рекомендуется использовать функцию contour3.
4. Расстояние от точки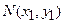 
до прямой 
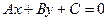определяется формулой 
.
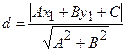5. Для формирования массива случайных элементов, распределенных по равномерному закону с заданным средним и дисперсией следует умножить данные, полученные с помощью функции rand на величину s и добавить к ним величину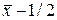 
, где .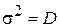
Содержание отчета:
· Титульный лист
· Задание на курсовую работу
· Основные теоретические сведения
· Схему алгоритма программы (если программа состоит из нескольких m-файлов – блок-схему программы и схемы алгоритмов каждого из файлов).
· Листинг программы
· Результаты расчетов и графики
Курсовая работа по дисциплине «Информатика»
Вариант 13
Часть 1. Среди множества случайных точек, расположенных в трехмерном пространстве, выбрать подмножество точек, лежащих внутри эллипсоида заданного размера, имеющего центр, совпадающий с началом координат.
Закон распределения каждой из координат случайных точек – нормальный с единичными средними и и дисперсиями.
Обеспечить ввод количества исходных точек и длин полуосей эллипсоида в командном окне системы MatLab. Построить трехмерный график, отображающий по выбору пользователя объемную фигуры и/или исходное множество точек и/или найденное подмножество контрастным цветом и типом. Отобразить точку, являющуюся центром тяжести исходного множества вторым контрастным цветом и типом. Предусмотреть возможность изменения исходных параметров и соответствующих им графиков в командном окне системы MatLab.
|
|
Часть 2. Среди множества случайных точек, расположенных на плоскости, выбрать подмножество точек, расстояние от которых до некоторой выбранной заранее прямой (координаты которой также являются случайными) не превышает заданной пороговой величины R. Обеспечить ввод количества исходных точек и величины R. Построить график, отображающий исходное множество точек и отметить на нем найденное подмножество контрастным цветом. Показать на графике прямую, расстояние до которой определяется программой. Предусмотреть возможность изменения исходных параметров и соответствующих им графиков непосредственно в графическом окне.
Справочные сведения
1. Уравнение эллипсоида 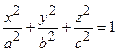, где a, b, c – полуоси.
2. Для формирования массива случайных элементов, распределенных по нормальному закону с заданным средним и дисперсией следует умножить данные, полученные с помощью функции randn на величину s и добавить к ним величину 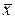, где .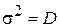
3. Для построение объемной фигуры рекомендуется использовать функцию contour3.
4. Расстояние от точки 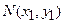до прямой 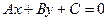определяется формулой .
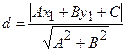5. Для формирования массива случайных элементов, распределенных по равномерному закону с заданным средним и дисперсией следует умножить данные, полученные с помощью функции rand на величину s и добавить к ним величину 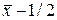, где .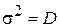
|
|
Содержание отчета:
· Титульный лист
· Задание на курсовую работу
· Основные теоретические сведения
· Схему алгоритма программы (если программа состоит из нескольких m-файлов – блок-схему программы и схемы алгоритмов каждого из файлов).
· Листинг программы
· Результаты расчетов и графики