Вариант 14
Часть 1. Среди множества случайных точек, расположенных в трехмерном пространстве, выбрать подмножество точек, расстояние от которых до некоторой выбранной заранее точки (координаты которой также являются случайными) не превышает заданной пороговой величины R. Обеспечить в командном окне системы MatLab:
v ввод количества исходных точек;
v величины R;
v выбор закона распределения координат случайных точек (равномерный или нормальный) и его параметры (среднее 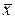 и дисперсию D).
и дисперсию D).
Построить трехмерный график, отображающий исходное множество точек и отметить на нем найденное подмножество контрастным цветом и типом. Показать на графике точку, расстояние до которой определяется программой вторым контрастным цветом и типом. Предусмотреть возможность изменения исходных параметров и соответствующих им графиков в командном окне системы Matlab.
Часть 2. Среди множества случайных точек, расположенных в трехмерном пространстве, выбрать подмножество точек, лежащих внутри сферы заданного радиуса, имеющей центр, совпадающий с центром тяжести исходного множества точек. Закон распределения каждой из координат случайных точек – нормальный с одинаковыми заданными пользователем средними 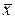 и дисперсиями D.
и дисперсиями D.
Обеспечить в графическом окне:
v ввод количества исходных точек,
v параметры распределения
v радиуса сферы R.
v построение трехмерного графика, отображающего по выбору пользователя сферу и/или исходное множество точек и/или найденное подмножество точек контрастным цветом и типом.
v отображение точки, являющейся центром тяжести исходного множества вторым контрастным цветом и типом.
Предусмотреть возможность изменения исходных параметров и соответствующих им графиков непосредственно в графическом окне.
|
|
Справочные сведения:
1. Расстояние между двумя точками 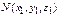 и
и 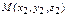 определяется формулой
определяется формулой 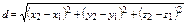 .
.
2. Для формирования массива случайных элементов, распределенных по равномерному закону с заданным средним и дисперсией следует умножить данные, полученные с помощью функции rand на величину s и добавить к ним величину 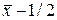 , где
, где 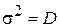 .
.
3. Для формирования массива случайных элементов, распределенных по нормальному закону с заданным средним и дисперсией следует умножить данные, полученные с помощью функции randn на величину s и добавить к ним величину 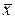 , где
, где 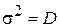 .
.
4. Уравнение. сферы, центр тяжести которой совпадает с началом координат 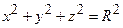 .
.
5. Для построение объемной фигуры рекомендуется использовать функцию contour3.
Содержание отчета:
· Титульный лист
· Задание на курсовую работу
· Основные теоретические сведения
· Схему алгоритма программы (если программа состоит из нескольких m-файлов – блок-схему программы и схемы алгоритмов каждого из файлов).
· Листинг программы
· Результаты расчетов и графики
Курсовая работа по дисциплине «Информатика»
Вариант 15
Часть 1. Среди множества случайных точек, расположенных в трехмерном пространстве, выбрать подмножество точек, лежащих за пределами сферы заданного радиуса, имеющей центр, совпадающий с центром трехмерной системы координат. Закон распределения каждой из координат случайных точек – равномерный с одинаковыми заданными пользователем средними 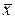 и дисперсиями D.
и дисперсиями D.
Обеспечить в графическом окне:
|
|
v ввод количества исходных точек,
v ввод параметров распределения
v ввод радиуса сферы R.
v построение трехмерного графика, отображающего по выбору пользователя сферу и/или исходное множество точек и/или найденное подмножество точек контрастным цветом и типом.
v отображение точки, являющейся центром тяжести трехмерной системы координат вторым контрастным цветом и типом.
Предусмотреть возможность изменения исходных параметров и соответствующих им графиков непосредственно в графическом окне.
Часть 2. Среди множества случайных точек, расположенных в трехмерном пространстве, выбрать подмножество точек, расстояние от которых до некоторой плоскости (параметры которой также являются случайными) не превышает заданной пороговой величины R. Обеспечить ввод количества исходных точек и величины R в командном окне системы MatLab. Построить трехмерный график, отображающий по выбору пользователя (в командном окне) плоскость и/или исходное множество точек и/или найденное подмножество контрастным цветом и типом. Предусмотреть возможность изменения исходных параметров и соответствующих им графиков в командном окне системы MatLab. Закон распределения каждой из координат случайных точек – нормальный со средним значением, равным двум и единичной дисперсией, равной 10.
Справочные сведения
1. Уравнение сферы 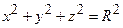 .
.
2. Расстояние от точки  до плоскости
до плоскости 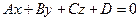 определяется формулой
определяется формулой 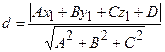 .
.
3. Для формирования массива случайных элементов, распределенных по равномерному закону с заданным средним и дисперсией следует умножить данные, полученные с помощью функции rand на величину s и добавить к ним величину 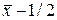 , где
, где 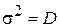 .
.
|
|
4. Для формирования массива случайных элементов, распределенных по нормальному закону с заданным средним и дисперсией следует умножить данные, полученные с помощью функции randn на величину s и добавить к ним величину 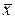 , где
, где 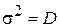 .
.
5. Для построение объемной фигуры рекомендуется использовать функцию contour3.
Содержание отчета:
· Титульный лист
· Задание на курсовую работу
· Основные теоретические сведения
· Схему алгоритма программы (если программа состоит из нескольких m-файлов – блок-схему программы и схемы алгоритмов каждого из файлов).
· Листинг программы
· Результаты расчетов и графики