Пусть  ,
, 
 – базис линейного пространства X над полем K. Тогда для любого вектора
– базис линейного пространства X над полем K. Тогда для любого вектора  ÎX справедливо равенство
ÎX справедливо равенство 

 = [A ]
= [A ] 
 .
.
Доказательство. Из следствия к теореме 1 получаем: 

 ([A ]
([A ] 
 ). Из определения координат
). Из определения координат
вектора в базисе  это и означает, что
это и означает, что 

 = [A ]
= [A ] 
 (1).
(1).
Выясним теперь, как изменится матрица линейного оператора A, если от базиса  пространства X мы перейдем к базису
пространства X мы перейдем к базису  того же пространства.
того же пространства.
Теорема 3. Пусть 
 и
и 
 базисы линейного пространства X над полем K. Для любого линейного оператора
базисы линейного пространства X над полем K. Для любого линейного оператора  справедливо равенство
справедливо равенство
[A ]  =
=  [A ]
[A ] 
 (2)
(2)
или, что то же самое [A ]  =
=  [A ]
[A ] 
 .
.
Доказательство. Обозначим  и
и 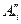
 - естолбцы матриц[A ]
- естолбцы матриц[A ]  и
и  [A ]
[A ] 
 соответственно, т.е. [A ]
соответственно, т.е. [A ]  =
=  и
и  [A ]
[A ] 
 =
=  . Очевидно, для того чтобы доказать равенство (2), достаточно доказать, что
. Очевидно, для того чтобы доказать равенство (2), достаточно доказать, что  для всех
для всех  , т.к. матрицы, стоящие в обеих частях равенства (2), имеют одинаковое строение. Рассмотрим столбец
, т.к. матрицы, стоящие в обеих частях равенства (2), имеют одинаковое строение. Рассмотрим столбец  . Из определения матрицы оператора
. Из определения матрицы оператора  в базисе
в базисе  получаем:
получаем:
 =[
=[ 
 ]
]  =
=  [
[ 
 ]
]  =
=  [
[  ]
]  [
[  ]
]  =(
=( [A ]
[A ] 
 )[
)[  ]
]  =
= 
для всех  , т.к. в координатном столбце вектора
, т.к. в координатном столбце вектора  в базисе
в базисе  число, стоящее на
число, стоящее на  - ом месте, равно единице, а остальные элементы равны нулю. Здесь мы также воспользовались известными формулами: [
- ом месте, равно единице, а остальные элементы равны нулю. Здесь мы также воспользовались известными формулами: [ 
 ]
]  =
=  [
[ 
 ]
]  и [
и [  ]
]  =
=  [
[  ]
]  и теоремой 2.
и теоремой 2.
Замечание. Напомним, что матрицы перехода связаны соотношениями  и
и 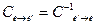 . Поэтому формула (2) может быть записана так: [A ]
. Поэтому формула (2) может быть записана так: [A ]  =
=  [A ]
[A ] 
 или так: [A ]
или так: [A ]  =
=  [A ]
[A ] 

Теорема 4. Пусть 
 – базис линейного пространства X над полем K. Для любых операторов
– базис линейного пространства X над полем K. Для любых операторов  и любых чисел l,
и любых чисел l,  Î K справедливы равенства:
Î K справедливы равенства:
1)  , т.е. матрица линейной комбинации двух линейных операторов в некотором базисе равна линейной комбинации матриц складываемых операторов в том же базисе и с теми же коэффициентами;
, т.е. матрица линейной комбинации двух линейных операторов в некотором базисе равна линейной комбинации матриц складываемых операторов в том же базисе и с теми же коэффициентами;
2)  , т.е. матрица произведения двух операторов в некотором базисе равна произведению матриц сомножителей в том же базисе и в том же порядке.
, т.е. матрица произведения двух операторов в некотором базисе равна произведению матриц сомножителей в том же базисе и в том же порядке.
Доказательство.
1. Обозначим 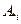 ,
,  и
и 
 - естолбцы матриц[A ]
- естолбцы матриц[A ]  ,
,  и
и  соответственно, т.е.
соответственно, т.е.
[A]  =
=  ,
,  =
=  и
и  =
=  .
.
Матрицы, стоящие в обеих частях равенства  имеют одинаковое строение. Следовательно, достаточно доказать, что
имеют одинаковое строение. Следовательно, достаточно доказать, что  Рассмотрим столбец
Рассмотрим столбец  . Из определения матрицы оператора
. Из определения матрицы оператора
 в базисе
в базисе  получаем:
получаем:

 для всех
для всех  . Здесь мы воспользовались свойствами координат вектора.
. Здесь мы воспользовались свойствами координат вектора.
Таким образом, первое равенство доказано.
2. Обозначим через  и
и 
 -е столбцы матриц
-е столбцы матриц  и
и  соответственно, т.е.
соответственно, т.е.  ,
,  .
.
Очевидно, интересующие нас матрицы имеют одинаковое строение, и, следовательно, равенство 2 будет доказано, если мы покажем, что 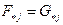 для всех
для всех  .
.

 ,
,
т.к. j-я координата вектора  в базисе
в базисе  равна 1, а остальные координаты – нули. Здесь мы воспользовались, помимо указанных соображений, определением умножения матриц и ассоциативностью умножения.
равна 1, а остальные координаты – нули. Здесь мы воспользовались, помимо указанных соображений, определением умножения матриц и ассоциативностью умножения.
Из теорем 1 и 4 вытекает следующая
Теорема 5. Линейно е пространство  линейных операторов, действующих в
линейных операторов, действующих в  - мерном
- мерном
пространстве X над полем K, изоморфно линейному пространству квадратных матриц  (K) порядка
(K) порядка  с элементами в K.
с элементами в K.
Доказательство. Покажем, что отображение 

 (K), заданное формулой
(K), заданное формулой 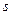 (
( ) =[A ]
) =[A ]  для любого
для любого  , где
, где  – базис линейного пространства X над K, является изоморфизмом линейных пространств.
– базис линейного пространства X над K, является изоморфизмом линейных пространств.
Как было доказано в теореме 1, 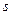 – взаимнооднозначное отображение. Из теоремы 4 следует:
– взаимнооднозначное отображение. Из теоремы 4 следует:  для любых
для любых  , и любых l,
, и любых l,  Î K. Следовательно,
Î K. Следовательно, 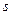 – изоморфизм линейных пространств.
– изоморфизм линейных пространств.
Следствие. Справедливо равенство  (K)=
(K)=  , т.к.
, т.к.  (K)=
(K)=  и
и  (K).
(K).
Замечание. Умножение матриц некоммутативное. Если бы для любых операторов  было бы справедливо равенство
было бы справедливо равенство  , то и для любых матриц
, то и для любых матриц 
 (K) выполнялось бы равенство
(K) выполнялось бы равенство  , что как известно, неверно.
, что как известно, неверно.