Поведение чисто вязкой жидкости описывается уравнением состояния, общая форма которого имеет вид:
τ = ηγ, (1)
где τ - напряжение сдвига, Па; η - динамическая вязкость, Па·с; γ - скорость сдвига 1/с.
При переходе от комплексной динамической вязкости к эффективной вязкости используют соотношение Кокса–Мерца.
Было установлено, что зависимость 
и 
практически совпадают, то есть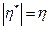 
при условии, что 
.
Два ученых, которые дали этому соотношению свое имя, эмпирически установили, что вязкость при стационарном сдвиге, измеренная в зависимости от скорости сдвига, может быть непосредственно связана с динамической комплексной вязкостью, измеренной как функция угловой скорости:
Было обнаружено, что соотношение справедливо для многих расплавов и растворов полимеров, но редко дает приемлемые результаты для суспензий.
Преимущество соотношения Кокса–Мерца состоит в том, что технически проще работать с частотой, чем со скоростями сдвига. На ротационных вискозиметрах невозможно проводить испытания расплавов и растворов полимеров при высоких скоростях сдвига из-за проявления эластичности – эффект Вайссенберга. Поэтому вместо измеренной кривой течения при стационарном сдвиге проще провести динамические испытания и использовать комплексную вязкость[1,2].
Для анализа полученных экспериментальных используют: степенной закон, модель Карро, температурную зависимость вязкости описывают уравнением Аррениуса или уравнением Рейнольдса[3].
Преимуществом степенного закона является его простота, малое число экспериментально определяемых постоянных, а недостатком – невозможность его использования в области величин скоростей сдвига близких к нулю, так как в этом случае большинство расплавов полимеров проявляют ньютоновский характер. Однако, область скоростей сдвига, характерных для переработки большинства полимеров, составляет (1–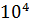 
) 
. В таком диапазоне изменения скоростей деформаций степенной закон достаточно адекватно описывает вязкостные свойства среды. Его аналитическое выражение:
|
|
, (2)
где m - коэффициент консистенции; n - показатель аномалии вязкости
Модель Карро в отличие от степенного закона позволяет описывать изменение вязкости от скорости сдвига в области очень малых скоростей сдвига. Аналитической выражение модели Карро имеет вид:
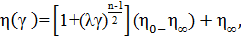(3)
где n - показатель аномалии вязкости; 
- константа; 
- вязкость при бесконечной скорости сдвига; 
- вязкость при нулевой скорости сдвига
Известно, что вязкость как ньютоновских, так и неньютоновских жидкостей зависят от температуры. Аналитический вид уравнения Аррениуса:
·exp(
, (4)
где T - температура; 
- энергия активации процесса течения; R - универсальная газовая постоянная; 
- значение коэффициента консистенции при температуре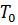 
. Аналитический вид уравнения Рейнольдса:
, (5)
где 
– температура; 
– температурный коэффициент вязкости; 
– значение коэффициента консистенции при температуре 
[1,4]..