Типовые звенья принято разделять на три основных группы:
Позиционные звенья. В эту группу входят идеальное усилительное (безинерционное) звено, апериодические звенья первого и второго порядка и колебательное звено. Все они обладают статической характеристикой вход- выход, т.е. при постоянном входном воздействии выходной сигнал отличается лишь масштабным коэффициентом. Идеальное усилительное звено с передаточной функцией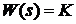 
не вносит частотных искажений в преобразуемый сигнал. Усилитель с ограниченной полосой пропускания чаще всего может быть описан передаточной функцией апериодического звена первого порядка, характеристики которого приведены ранее.
Апериодическое звено второго порядка и колебательное звено имеют одинаковый вид передаточной функции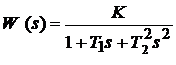 
и различаются типом корней полинома в знаменателе функции. При условии 
корни вещественные. В случае пары комплексно-сопряженных корней звено называется колебательным, а его передаточную функцию, вводя параметр затухания 
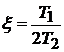, записывают в виде 
.
Подстановкой 
получим АЧХ и ФЧХ звена 
, 
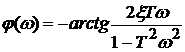. Анализ на экстремум показывает, что при значениях 
резонанс отсутствует. Максимум АЧХ при 
меньше 0.707 соответствует частоте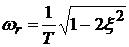 
. Построение ЛАЧХ дает значение 
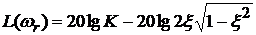. Поправка составляет 1.25 дБ для значения 
и становится заметной (около 3 дБ) лишь при 
. Заметим, что крутизна ЛФЧХ уже при этих значениях существенно выше, чем у апериодического звена второго порядка. Резонансные явления на переходной характеристике оценивают по величине первого выброса (измеряется в процентах по отношению к установившемуся значению) и количеству периодов колебаний до завершения переходного процесса. Принято [Л.1] фиксировать длительность последнего по уровню 5% отклонения от установившегося значения.
Интегрирующие звенья. В эту группу входят инерционный интегратор и два идеализированных звена – идеальный интегратор и пропорционально-интегрирующее звено.
Идеальный интегратор характеризуется передаточной функцией 
, где 
– постоянная интегрирования (коэффициент усиления 
). АФХ имеет вид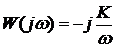 
, при этом ЛАЧХ 
представляет собой прямую с наклоном –20 дБ/дек, а ЛФЧХ 
.
Пропорционально-интегрирующее (ПИ) звено представляет собой параллельное соединение идеального интегратора с безинерционным звеном с коэффициентом передачи 
. Передаточная функция ПИ-звена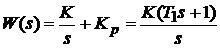 
. Здесь сопрягающая частота 
определяет свойства звена. На частотах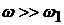 
значение ЛФЧХ 
, а высокочастотная асимптота ЛАЧХ соответствует уровню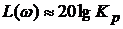 
.
Практическая реализация идеального интегрирования в широкой полосе частот затруднительна, поэтому для более точного описания свойств интеграторов нужно ввести дополнительную инерционность. Инерционный интегратор характеризуется передаточной функцией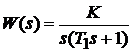 
, где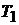 
– постоянная времени, учитывающая инерционность. Особенности свойств инерционного интегратора ясны из описания его частотных характеристик: 
, 
.
Импульсную переходную характеристику получим обратным преобразованием Лапласа передаточной функции 
. По таблице стандартных преобразований Лапласа [Л.2] находим 
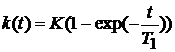. Переходную характеристику проще всего определить интегрированием весовой функции: 
.
Дифференцирующие звенья.
Идеальное дифференцирующее звено с передаточной функцией 
формирует производную от входного сигнала. Переходная характеристика представляет собой дельта функцию.
Обеспечить дифференцирование в бесконечно широкой полосе частот невозможно, поэтому обычно рассматривают практически реализуемый вариант – инерционное дифференцирующее звено. Передаточная функция принимает вид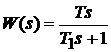 
. Переходная характеристика будет по форме совпадать с импульсной переходной характеристикой апериодического звена первого порядка.
Форсирующее звено (пропорционально дифференцирующее или дифференцирующее звено первого порядка) с передаточной функцией 
является идеализированным вариантом, который структурно соответствует суммированию сигнала с его производной.
Практически реализуемый вариант описывают передаточной функцией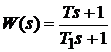 
, причем при условии 
звено обладает дифференцирующими свойствами в широкой полосе частот.
Передаточные функции рассмотренных групп звеньев не имеют нулей и полюсов в правой полуплоскости. Такие звенья принято называть минимально-фазовыми. Важнейшим их свойством является возможность определить с помощью преобразования Гильберта вещественной части АФХ ее мнимую часть и наоборот. Аналогичное соответствие имеют также АЧХ и ФЧХ.