V этап: Введение понятия объема призмы

Цель: Углубить у учащихся интуитивно-наглядное понятие объема пространственных фигур.

Оборудование: модели призм.

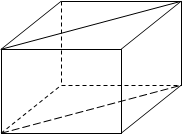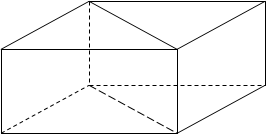Разрежьте (пластилиновую модель призмы, плоскостью проходящей через диагональ основания. Какие получили фигуры?

В результате выполнения этого упражнения ученики получили две призмы с равными основаниями (основанием является прямоугольный треугольник), а все остальные соответствующие элементы призмы равны.

Упражнение 2: Как вычислить объем каждой из полученных призм?

Вывод: Каждая из полученных призм имеет объем равный половине объема данного параллелепипеда. (Объем параллелепипеда умеют вычислять в пятом классе).

Упражнение 3:

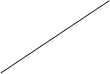
Дана призма, в основании которой треугольник. Как вычислить объем этой призмы?

Учащиеся умеют вычислять объем призмы основанием которой является

прямоугольный треугольник.

Важно, чтобы учащиеся увидели в этом упражнении предыдущее. Объем данной призмы есть сумма объемов двух призм, основаниями которых являются прямоугольные треугольники.

Затем предлагается вычислить объем призмы основание которой трапеция, или любой

другой произвольной формы.

V = S_осн h

Сборник задач

Задача 1: Запомните пропуски.

В правильной треугольной призме сторона основания равна a, боковое ребро 2a. Найти площадь сечения, проведенного через сторону одного и центр другого основания.

Дано:

АВСА₁В₁С₁ – произвольная призма

АВ = а

АА₁ = 2а

S_сеч =?

Решение:

1) Плоскость сечения α определяют прямая … и точка …; проведем сечение.

2) ВС ׀׀ В₁С₁, значит …

3) α ВС ׀׀ А₁В₁С₁, значит, линия пересечения В₂С₂ …

4) секущая плоскость α имеет с гранью АА₁В₁В две общие точки В и В₂, значит …; а с гранью АА₁С₁С – точки С и С₂, значит …;

5) сечение ВВ₂С₂С – …, т.к. …;

6) находим высоту О₁D трапеции ВВ₂С₂С, ОD _┴ ВС

7) О₁D_┴ …

8) 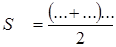; ВС = а

9) В₂С₂ =?; Δ А₁В₂С₂ …

10) = …

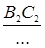11) 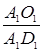= … (медиана в точке пересечения …)

12) = …; = ….

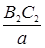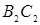13) Из ΔОО₁D: О₁D²= … + … (…)

14) АD = a sin … = …; OD = 1/3 … = …;

15) О₁D² = … = … = …; О₁D = … = …

16) S_cеч =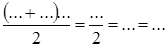

Задача 2: В прямоугольной призме стороны основания равны 5 см, 6 см, 7 см, сечение проведенное через среднюю сторону одного основания и противоположную вершину другого, составляет с основанием угол в 60^о. Найти площадь полной поверхности призмы.

Решение: S_п = S_б + 2 S_осн (1)

1) S_б =? S_б = Р l (2), Р = … + … +… = …; 2) из ΔADA₁ имеем l = AD … (3);

3) AD - высота ΔAВС, 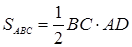(4);

4) 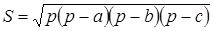, а = 5 см, b = 6 см, c = … p = ½ … = …

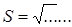5) подставим в (4) найденное значение S и ВС: 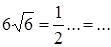, АD = …

6) подставим в (3) значение AD и tg 60^о: l = … = …; 7) подставим в (2) значения P и l: S_б = … = …; 8) подставим в (1) значения S_б и S_осн: S_п = … + … ≈ ….

Задача 3: В прямоугольном параллелепипеде сторона основания равна а и составляет с диагональю основания угол α, а с диагональю грани, которой принадлежит сторона, угол β. Найти площадь боковой поверхности.

Решение: 1) S_б = Р l (2), 2) Р = 2 (… + …); AD = а; 3) АВ =? из ΔAВD имеем АВ = … =… (катет равен …); 4) Р = 2 (…+…) = … = … = … = … 5) l =? из ΔAА₁D имеем AА₁ = АD…=…; 6) S_б = … = ….

1) Будет ли сечение, перпендикулярное к боковому ребру призмы, перпендикулярно к ее боковой грани?

2) Боковое ребро призмы образует равные острые углы с прилежащими сторонами основания. Что следует сказать о проекции этого ребра на плоскость основания?

3) Показать на чертеже расстояние ребра куба от пересекающейся с ним диагоналями куба.

4) Показать в кубе расстояние между а) диагональю основания и перпендикулярной к ней диагональю куба; б) непересекающимися диагоналями непересекающихся граней.

Задача 4: Основанием призмы служит правильный ΔAВС со стороной а, вершина А₁ проецируется в центр нижнего основания и ребро АА₁ составляет со стороной снования АВ угол 45^о. Найти объем.