Системы счисления
Система счисления — это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Существуют системы позиционные и непозиционные. В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти. В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число. Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления — это количество различных знаков или символов, используемых для изображения цифр в данной системе. За основание можно принять любое натуральное число — два, три, четыре, шестнадцать и т. д. Следовательно, возможно бесконечное множество позиционных систем.
Десятичная система счисления
Эта система пришла в Европу из Индии, где она появилась не позднее VI века н. э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени; 10, 100, 1000 и т. д. Крайняя правая цифра числа показывает число единиц, вторая справа — число десятков, следующая — число сотен и т. д. Причина наибольшей распространенности десятичной системы счисления состоит в том, что первым счетным аппаратом человека являлись его руки. Число пальцев и стало отправным пунктом для системы счета.
Двоичная система счисления
В этой системе всего две цифры — 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Крайняя правая цифра числа показывает число единиц, следующая цифра — число двоек, следующая — число четверок и т. д. Двоичная система счисления позволяет закодировать любое натуральное число — представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.
Восьмеричная система счисления
В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает — как и в десятичном числе — просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем 64 и т. д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: А, В, С, D, Е, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем разряде — 16 (десятичное), в следующем — 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
Способы перевода чисел из одной системы счисления в другую.
Перевод чисел из одной позиционной системы счисления в другую: перевод целых чисел.
Чтобы перевести целое число из одной системы счисления с основанием d1 в другую с основанием d2 необходимо последовательно делить это число и получаемые частные на основание d2 новой системы до тех пор, пока не получится частное меньше основания d2. Последнее частное – старшая цифра числа в новой системе счисления с основанием d2, а следующие за ней цифры - это остатки от деления, записываемые в последовательности, обратной их получению. Арифметические действия выполнять в той системе счисления, в которой записано переводимое число.
Пример 1. Перевести число 11(10) в двоичную систему счисления.
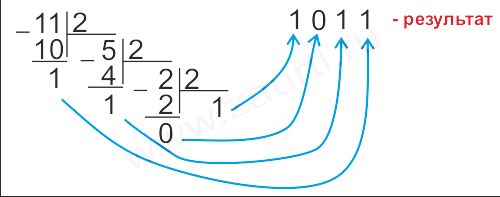
Ответ: 11(10)=1011(2).
Пример 2. Перевести число 122(10) в восьмеричную систему счисления.
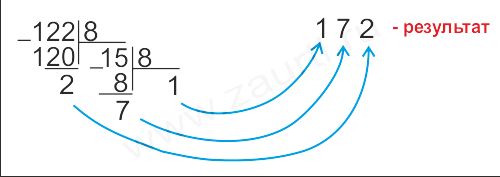
Ответ: 122(10)=172(8).
Пример 3. Перевести число 500(10) в шестнадцатеричную систему счисления.
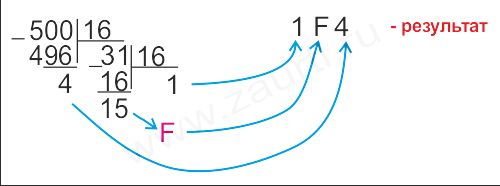
Ответ: 500(10)=1F4(16).
Перевод чисел из одной позиционной системы счисления в другую: перевод правильных дробей.
Чтобы перевести правильную дробь из системы счисления с основанием d1 в систему с основанием d2, необходимо последовательно умножать исходную дробь и дробные части получающихся произведений на основание новой системы счисления d2. Правильная дробь числа в новой системе счисления с основанием d2 формируется в виде целых частей получающихся произведений, начиная с первого.
Если при переводе получается дробь в виде бесконечного или расходящегося ряда, процесс можно закончить при достижении необходимой точности.
При переводе смешанных чисел, необходимо в новую систему перевести отдельно целую и дробную части по правилам перевода целых чисел и правильных дробей, а затем оба результата объединить в одно смешанное число в новой системе счисления.
Пример 1. Перевести число 0,625(10) в двоичную систему счисления.
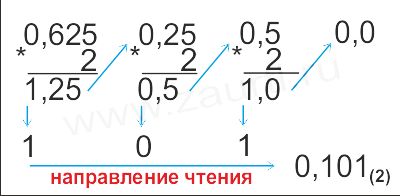
Ответ: 0,625(10)=0,101(2).
Пример 2. Перевести число 0,6(10) в восьмеричную систему счисления.
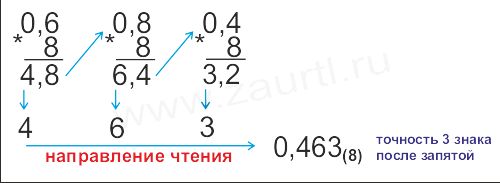
Ответ: 0,6(10)=0,463(8).
Пример 2. Перевести число 0,7(10) в шестнадцатеричную систему счисления.
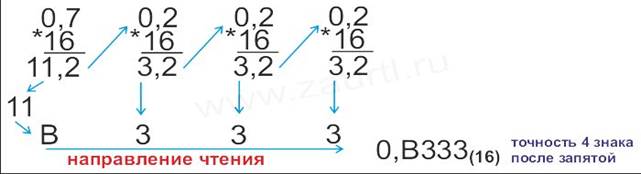
Ответ: 0,7(10)=0,В333(16).
Перевод двоичных, восьмеричных и шестнадцатеричных чисел в десятичную систему счисления.
Для перевода числа P-ичной системы в десятичную необходимо использовать следующую формулу разложения:
аnan-1…а1а0=аnPn+ аn-1Pn-1+…+ а1P+a0.
Пример 1. Перевести число 101,11(2) в десятичную систему счисления.
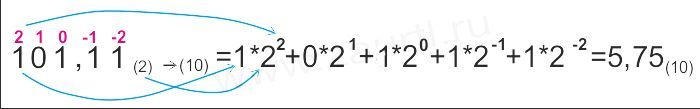
Ответ: 101,11(2)= 5,75(10).
Пример 2. Перевести число 57,24(8) в десятичную систему счисления.
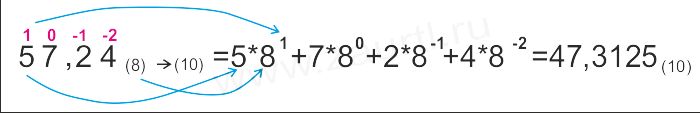
Ответ: 57,24(8) = 47,3125(10).
Пример 3. Перевести число 7A,84(16) в десятичную систему счисления.
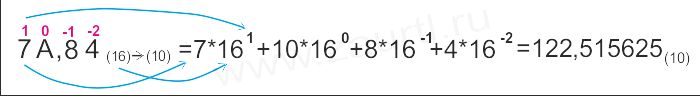
Ответ: 7A,84(16)= 122,515625(10).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления и обратно.
Для перевода числа из восьмеричной системы счисления в двоичную необходимо каждую цифру этого числа записать трехразрядным двоичным числом (триадой).
Пример: записать число 16,24(8) в двоичной системе счисления.
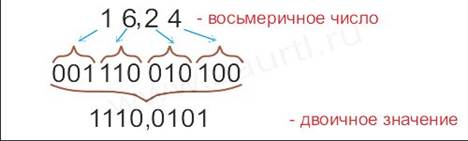
Ответ: 16,24(8)= 1110,0101(2).
Примечание: незначащие нули слева для целых чисел и справа для дробей не записываются.
Для обратного перевода двоичного числа в восьмеричную систему счисления, необходимо исходное число разбить на триады влево и вправо от запятой и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняют нулями.
Пример: записать число 1110,0101(2) в восьмеричной системе счисления.
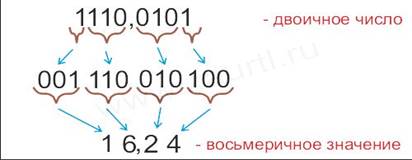
Ответ: 1110,0101(2)= 16,24(8).
Для перевода числа из шестнадцатеричной системы счисления в двоичную необходимо каждую цифру этого числа записать четырехразрядным двоичным числом (тетрадой).
Пример: записать число 7A,7E(16) в двоичной системе счисления.

Ответ: 7A,7E(16)= 1111010,0111111(2).
Примечание: незначащие нули слева для целых чисел и справа для дробей не записываются.
Для обратного перевода двоичного числа в шестнадцатеричную систему счисления, необходимо исходное число разбить на тетрады влево и вправо от запятой и представить каждую группу цифрой в шестнадцатеричной системе счисления. Крайние неполные триады дополняют нулями.
Пример: записать число 1111010,0111111(2) в шестнадцатеричной системе счисления.
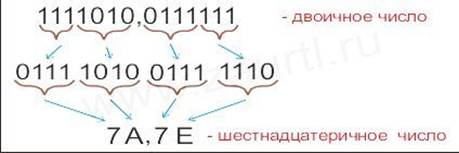
Ответ: 1111010,0111111(2)= 7A,7E(16).
1) Системы счисления.
Система счисления – совокупность правил наименования и изображения чисел с помощью набора символов, называемых цифрами.
Или
Система счисления - способ кодирования числовой информации, т.е. способ записи чисел с помощью некоторого алфавита, символы которого называют цифрами.
Системы счисления делятся на позиционные и непозиционные.
Пример непозиционной системы счисления – римская: несколько чисел приняты за основные (1-I, 5-V, 10-X, 50- L, 100-C, 500-D, 1000-M), а остальные получаются из основных путем сложения (как VI, VII) или вычитания (как IV, IX).
К позиционным системам счисления относятся двоичная, десятичная, восьмеричная, шестнадцатеричная. Здесь любое число записывается последовательностью цифр соответствующего алфавита, причем значение каждой цифры зависит от места (позиции), которое она занимает в этой последовательности. Например, в записи 555, сделанной в десятичной системе счисления, использована одна цифра 5, но в зависимости от занимаемого ею места она имеет разное количественное значение – 5 единиц, 5 десятков или 5 сотен. Поэтому справедливы равенства (подстрочные индексы применим для указания, в какой системе счисления записано число):
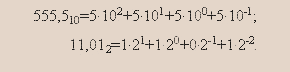
2) Двоичная система счисления.
Алфавит двоичной системы счисления состоит из цифр 0 и 1.
Перевод числа из десятичной системы счисления в двоичную.
Перевод целых чисел. Пусть требуется найти представление числа 1210 в двоичной системе счисления (задание может быть сформулировано и так: перевести число 12 из десятичной в двоичную систему счисления, или
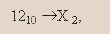
где Х заменяет искомое представление).
Поступаем следующим образом: делим, начиная с 12, каждое получающееся частное на основание системы, в которую переводим число, то есть на 2. Получаем
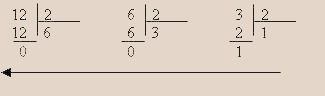
Затем в направлении, указанном стрелкой, начиная с последнего частного (в нашем случае оно всегда будет равно 1), записываемого в старший разряд формируемого двоичного представления, фиксируем все остатки. В итоге получаем ответ:
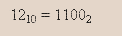
Перевод десятичных дробей, меньших единицы. Если указанный перевод необходимо осуществить для числа меньше единицы, допустим для 0,25, то схема наших действий изменится:
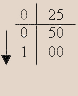
Для удобства проведем вертикальную линию, отделяющую целую часть от дробной. Умножим, оказавшуюся слева дробную часть на 2. Результат записываем на следующей строке, причем оставляем справа от вертикали столько разрядов, сколько было у исходной дробной части. Так как при этом произведение равно 50, то в разряд слева от вертикали записываем 0. Повторяем процесс умножения на 2 числа, стоящего справа от вертикали. Результат умножения 50 на 2 равен 100. Следовательно, при записи результата в следующую строку схемы справа от вертикали оказываются два нуля, а единица переносится в разряд слева от вертикали. На этом процесс умножения на 2 в данном примере заканчивается, так как мы уже получили точный ответ. Ответ образует число, прочитываемое слева от вертикали в направлении, указанном стрелкой (сверху вниз). Очевидно, что, если продолжать умножение дальше, вы должны были бы умножать на 2 нули справа от вертикали и, следовательно, в каждой строке слева от вертикали записывать только нули. Эго были бы незначащие нули в получаемой дроби. Поэтому, получив в результате серии умножений на 2 справа от вертикали одни нули, мы заканчиваем процесс перевода десятичного дробного числа меньше единицы в двоичную систему счисления и записываем ответ:
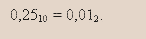
Понятно, что гораздо чаще мы встретим такую исходную десятичную дробь, когда умножение на 2 чисел, стоящих справа от вертикали, не приведет к появлению там одних лишь нулей. Пусть, например, по условию задачи требуется перевести в двоичную систему счисления десятичную дробь 0,3. Поступаем описанным выше образом:
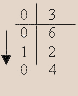
В этом случае точный ответ не может быть получен, так как процесс перевода приходится оборвать и записать с некоторой заданной точностью приблизительный ответ (конкретно в этом примере до трех знаков после запятой):
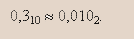
Перевод десятичных дробей больше единицы. В этом случае необходимо, отделив в исходном десятичном числе целую и дробную части, провести для каждой из них независимый перевод в двоичную систему счисления указанным выше способом. Рассмотрим два примера, используя уже полученные результаты:
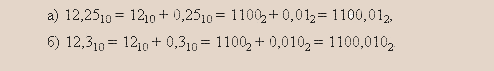
В примере
а) ответ получен точным, тогда как в примере
б) из-за приблизительности перевода дробной части окончательный ответ получается также приближенным.
Перевод числа из двоичной системы счисления в десятичную. Это перевод – как бы обратный к изложенному выше. Его наиболее просто осуществить, основываясь на позиционности двоичной системы счисления. Уже отмечалась правомерность записи двоичного числа в виде суммы степеней основания системы счисления, то есть степеней двойки. Сделав такую запись, надо подсчитать десятичное значение полученной суммы:
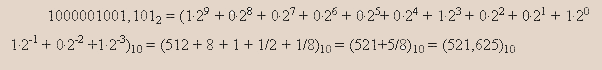
Наконец, остановимся на преимуществах и недостатках использования двоичной системы счисления по сравнению с любой другой позиционной системой счисления. К недостаткам относится длина записи, представляющей двоичное число. Основные преимущества – простота совершаемых операций, а также возможность осуществлять автоматическую обработку информации, реализуя только два состояния элементов компьютера.