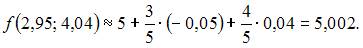Тема: Частные производные первого порядка
Частная производная  функции
функции 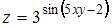 имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
При вычислении частной производной  по переменной y переменную x рассматриваем как постоянную величину. Тогда
по переменной y переменную x рассматриваем как постоянную величину. Тогда

Тема: Частные производные первого порядка
Частная производная 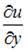 функции
функции 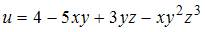 имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
При вычислении частной производной 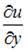 по переменной y переменные x и z рассматриваем как постоянные величины. Тогда
по переменной y переменные x и z рассматриваем как постоянные величины. Тогда

Тема: Частные производные высших порядков
Частная производная второго порядка  функции
функции 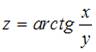 имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
При вычислении частной производной функции  по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
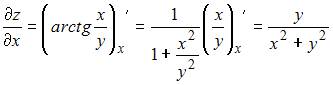 и
и

Тема: Дифференциальное исчисление ФНП
Значение частной производной  функции
функции 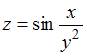 в точке
в точке  равно …
равно …

| 
| ||

| |||
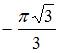
| |||
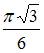
|
Решение:
При вычислении частной производной  по переменной
по переменной  переменную
переменную 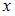 рассматриваем как постоянную величину. Тогда
рассматриваем как постоянную величину. Тогда
 .
.
Следовательно,  .
.
Тема: Частные производные первого порядка
Частная производная  функции
функции  имеет вид …
имеет вид …

| 
| ||

| |||
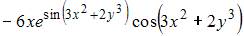
| |||

|
Решение:
При вычислении частной производной  по переменной x переменную y рассматриваем как постоянную величину. Тогда
по переменной x переменную y рассматриваем как постоянную величину. Тогда
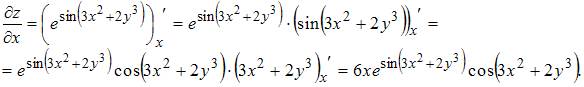
Тема: Частные производные первого порядка
Частная производная  функции
функции  имеет вид …
имеет вид …

| 
| ||
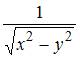
| |||

| |||

|
Решение:
При вычислении частной производной  по переменной y переменную x рассматриваем как постоянную величину. Тогда
по переменной y переменную x рассматриваем как постоянную величину. Тогда
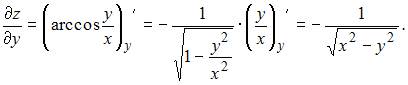
Тема: Частные производные высших порядков
Дана функция 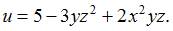 Тогда производная
Тогда производная  равна …
равна …

| 
| ||
| 4 ху | |||
| – 6 у | |||

|
Решение:
Частные производные функции двух и более переменных вычисляются по тем же формулам и правилам, что и функции одной переменной. Следует помнить только одно правило: если вычисляем частную производную по одной переменной, то остальные переменные считаются постоянными величинами.
Если  то
то  Так как
Так как  то
то 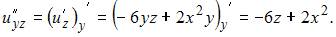
Тема: Частные производные высших порядков
Частная производная второго порядка  функции
функции  имеет вид …
имеет вид …

| 
| ||

| |||

| |||

|
Решение:
При вычислении частной производной функции  по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда

Тема: Частные производные высших порядков
Частная производная второго порядка  функции
функции 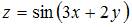 имеет вид …
имеет вид …

| 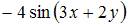
| ||

| |||
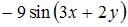
| |||

|
Решение:
При вычислении частной производной функции  по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
 и
и

Тема: Частные производные высших порядков
Значение производной второго порядка функции 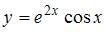 при
при  равно …
равно …

| 
| ||

| |||
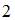
| |||

|
Решение:
Вычислим производную первого порядка:
 .
.
Тогда производная второго порядка вычисляется как производная от производной первого порядка, то есть

Следовательно,  .
.
Тема: Частные производные высших порядков
Частная производная второго порядка  функции
функции 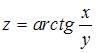 имеет вид …
имеет вид …

| 
| ||
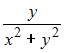
| |||

| |||

|
Решение:
При вычислении частной производной функции  по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
по одной из переменных другую переменную рассматриваем как постоянную величину. Тогда
 и
и

Тема: Полный дифференциал
Приближенное значение функции  в точке
в точке  вычисленное с помощью полного дифференциала, равно …
вычисленное с помощью полного дифференциала, равно …

| 5,002 | ||
| 5,02 | |||
| 5,062 | |||
| 5,001 |
Решение:
Воспользуемся формулой 
где 


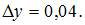
Вычислим последовательно
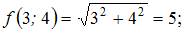

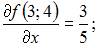
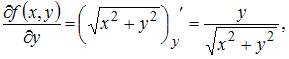

Тогда