СТАТИКА
Задача С1
Жесткая рама, расположенная в вертикальной плоскости (рис. С1.0 - С1.9, табл. С1), закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню с шарнирами на концах, или к шарнирной опоре на катках.
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом 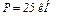 . На раму действуют пара сил с моментом
. На раму действуют пара сил с моментом 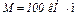 и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях № 1 на раму действует сила
и две силы, значения, направления и точки приложения которых указаны в таблице (например, в условиях № 1 на раму действует сила 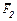 под углом 15° к горизонтальной оси, приложенная в точке D, и сила
под углом 15° к горизонтальной оси, приложенная в точке D, и сила 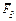 под углом 60° к горизонтальной оси, приложенная в точке E, и т.д.).
под углом 60° к горизонтальной оси, приложенная в точке E, и т.д.).
Определить реакции связей в точках A, В, вызываемые действующими нагрузками. При окончательных расчетах принять а = 0,5 м.
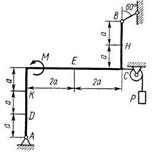
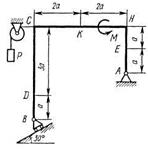
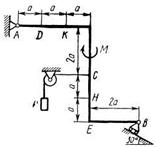
Рис. С1.0 Рис. С1.1 Рис.С1.2
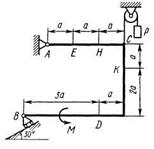
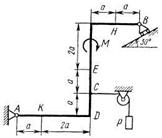
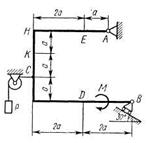
Рис. С1.3 Рис. С1.4 Рис.С1.5
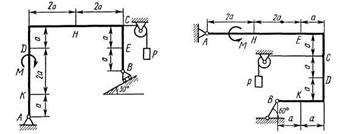
Рис. С1.6 Рис. С1.7
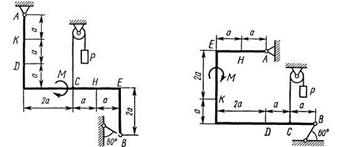
Рис. С1.8 Рис. С1.9
Таблица С1
| Силы | 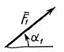
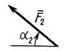
| 
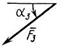
| 
| 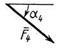
| ||||
| F1 = 10 кН | F2 = 20 кН | F3 = 30 кН | F4 = 40 кН | |||||
| Номер условия | Точка приложения | α1, град | Точка приложения | α2, град | Точка приложения | α3, град | Точка приложения | α4, град |
| Н — К — D — Е — Н — | — — — — — | — D — К — Н — D — Е | — — — — — | — Е — Н — — К — D К | — — — — — | К — Е — Е D — Н — — | — — — — — |
Указания. Задача С1 - на равновесие тела под действием произвольной плоской системы сил. При ее решении учесть, что натяжения обеих ветвей нити, перекинутой через блок, когда трением пренебрегают, будут одинаковыми. Уравнение моментов будет более простым (содержать меньше неизвестных), если брать моменты относительно точки, где пересекаются линии действия двух реакций связей. При вычислении момента силы 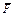 часто удобно разложить ее на составляющие
часто удобно разложить ее на составляющие 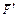 и
и 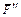 , для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда
, для которых плечи легко определяются, и воспользоваться теоремой Вариньона; тогда
mo(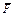 ) = mo(
) = mo(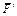 ) + mo(
) + mo(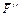 ).
).
|
|
Пример С1. Жесткая пластина ABCD (рис. С1) имеет в точке А неподвижную шарнирную опору, а в точке В — подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке.
Дано: F = 25 кH, a = 60°, Р = 18 кН, g = 75°, М = 50 кНм, b = 30°, а = 0,5 м.
Определить: реакции в точках А и В, вызываемые действующими нагрузками.
Решение. 1. Рассмотрим равновесие пластины. Проведем координатные оси ху и изобразим действующие на пластину силы: силу F, пару сил с моментом M, натяжение троса 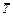 (по модулю Т = Р) и реакции связей
(по модулю Т = Р) и реакции связей 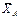 ,
, 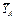 ,
, 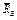 (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
(реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
2. Для полученной плоской системы сил составим три уравнения равновесия. При вычислении момента силы 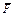 относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силу
относительно точки А воспользуемся теоремой Вариньона, т.е. разложим силу 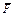 на составляющие
на составляющие 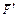 ,
, 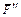 (
(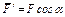 ,
, 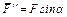 ) и учтем, что
) и учтем, что 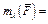
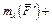
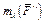 .
.
Получим:
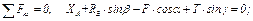 (1)
(1)
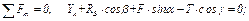 (2)
(2)
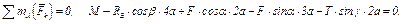 (3)
(3)
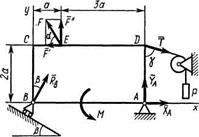
Рис. С1
Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции.
Ответ: 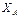 = - 8,5 кН;
= - 8,5 кН; 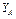 = - 23,3 кН;
= - 23,3 кН; 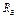 = 7,3 кН. Знаки указывают, что силы
= 7,3 кН. Знаки указывают, что силы 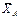 и
и 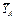 направлены противоположно показанным на рис. С1.
направлены противоположно показанным на рис. С1.
Задача С2
Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром (или подпятником) в точке А, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис. С2.0 – С2.7) или же двумя подшипниками в точках А и В и двумя невесомыми стержнями 1 и 2 (рис. С2.8, С2.9); все стержни прикреплены к плитам и к неподвижным опорам шарнирами.
|
|
Размеры плит указаны на рисунках; вес большей плиты 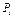 = 5 кН, вес меньшей плиты
= 5 кН, вес меньшей плиты 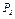 = 3 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость ху — горизонтальная).
= 3 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость ху — горизонтальная).
На плиты действуют пара сил с моментом М = 4 кН·м, лежащая в плоскости одной из плит, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С2; при этом силы 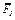 и
и 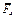 лежат в плоскостях, параллельных плоскости ху, сила
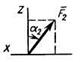
лежат в плоскостях, параллельных плоскости ху, сила
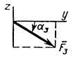
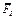 — в плоскости, параллельной xz, и сила
— в плоскости, параллельной xz, и сила 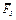 — в плоскости, параллельной yz. Точки приложения сил (D, Е, Н, К) находятся в углах или в серединах сторон плит.
— в плоскости, параллельной yz. Точки приложения сил (D, Е, Н, К) находятся в углах или в серединах сторон плит.
Определить реакции связей в точках А и В и реакцию стержня (стержней). При подсчетах принять а= 0,6 м.
Указания. Задача С2 — на равновесие тела под действием произвольной пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) — две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы 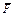 часто удобно разложить ее на две составляющие
часто удобно разложить ее на две составляющие 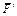 и
и 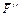 , параллельные координатным осям (или на три); тогда, по теореме Вариньона, mx(
, параллельные координатным осям (или на три); тогда, по теореме Вариньона, mx(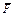 )= mx(
)= mx(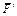 )+ mx(
)+ mx(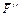 ) и т.д.
) и т.д.
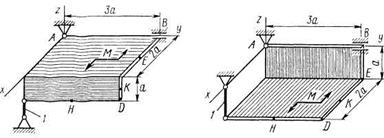
Рис. С2.0 Рис. С2.1
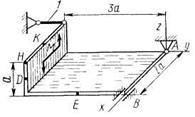
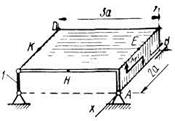
Рис. С2.2 Рис. С2.3
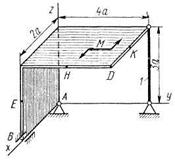
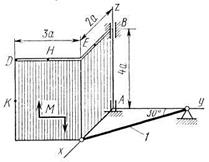
Рис. С2.4 Рис. С2.5
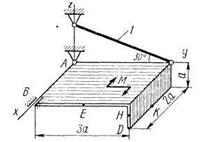
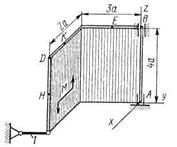
Рис. С2.6 Рис. С2.7
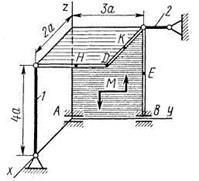
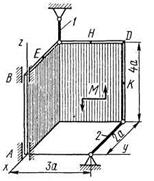
Рис. С2.8 Рис. С2.9
Таблица С2
| Силы | 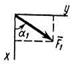
| 
| 
| 
| ||||
| F1 = 6 кН | F2 = 8 кН | F3 = 10 кН | F4 = 12 кН | |||||
| Номер условия | Точка приложения | α1, град | Точка приложения | α2, град | Точка приложения | α3, град | Точка приложения | α4, град |
| E — — K — H — — D — | — — — — — — | H D — — E K H — — D | — — — — | — Е K D — — D H К — | — — — — | — — Е — D — — K — H | — — — — — — |
|
|
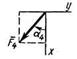
Пример С2. Горизонтальная прямоугольная плита весом Р (рис. С2) закреплена сферическим шарниром в точке А, цилиндрическим (подшипником) в точке В и невесомым стержнем DD'. На плиту в плоскости, параллельной xz, действует сила 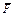 , а в плоскости, параллельной yz, — пара сил с моментом М.
, а в плоскости, параллельной yz, — пара сил с моментом М.
Дано: Р = 3 кН, F = 8 кН, М = 4 кН·м, 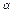 = 60°, AС = 0,8 м, АВ = 1,2 м,
= 60°, AС = 0,8 м, АВ = 1,2 м,
BE = 0,4 м, ЕН = 0,4 м.
Определить: реакции опор A, В истержня DD'.
Решение. 1.Рассмотрим равновесие плиты. На плиту действуют (рис.С2) заданные силы 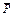 ,
, 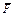 и пара с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие
и пара с моментом М, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие 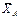 ,
, 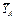 ,
, 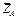
 цилиндрического (подшипника) — на две составляющие
цилиндрического (подшипника) — на две составляющие 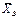 ,
, 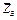 (в плоскости, перпендикулярной оси подшипника); реакцию
(в плоскости, перпендикулярной оси подшипника); реакцию 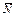 стержня направляем вдоль стержня от D к D', предполагая, что он растянут.
стержня направляем вдоль стержня от D к D', предполагая, что он растянут.
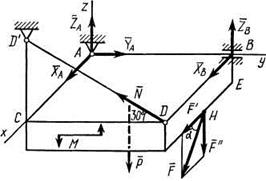
Рис. С2
2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:
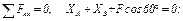 (1)
(1)
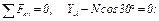 (2)
(2)
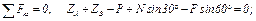 (3)
(3)
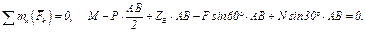 (4)
(4)
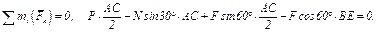 (5)
(5)
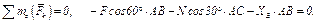 (6)
(6)
Для определения моментов силы 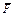 относительно осей разлагаем ее на составляющие
относительно осей разлагаем ее на составляющие 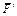 и
и 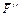 параллельные осям х и z (
параллельные осям х и z (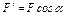 ,
, 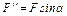 ), и применяем теорему Вариньона (см. «Указания»). Аналогично можно поступить при определении моментов реакции
), и применяем теорему Вариньона (см. «Указания»). Аналогично можно поступить при определении моментов реакции 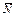 .
.
Подставив в составленные уравнения числовые значения всех заданных величин и решив эти уравнения, найдем искомые реакции.
Ответ: 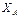 = 3,4 кН;
= 3,4 кН; 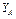 = 5,1 кН;
= 5,1 кН; 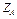 = 4,8 кН;
= 4,8 кН; 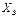 = 7,4 кН;
= 7,4 кН; 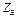 = 2,1 кН;
= 2,1 кН;
N = 5,9 кН. Знак минус указывает, что реакция 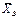 направлена противоположно показанной на рис. С2.
направлена противоположно показанной на рис. С2.
КИНЕМАТИКА
Задача К1
Под номером К1 помещены две задачи К1а и К1б, которые надо решить.
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = 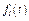 , у =
, у = 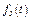 , где х и у выражены в сантиметрах, t — в секундах.
, где х и у выражены в сантиметрах, t — в секундах.
Таблица К1
| Номер условия | 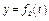
| 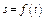
| ||
| рис. 0-2 | рис. 3-6 | рис. 7-9 | ||
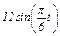
| 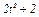
| 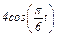
| 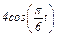
| |
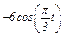
| 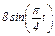
| 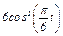
| 
| |
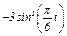
| 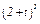
| 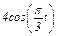
| 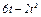
| |
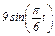
| 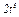
| 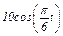
| 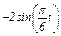
| |
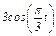
| 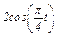
| 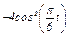
| 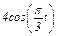
| |
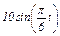
| 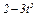
| 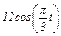
| 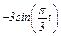
| |
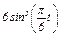
| 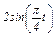
| 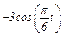
| 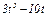
| |
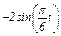
| 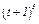
| 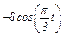
| 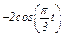
| |
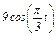
| 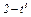
| 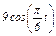
| 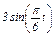
| |
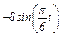
| 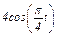
| 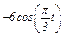
| 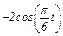
|
Найти уравнение траектории точки; для момента времени 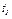 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
= 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость x = 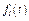 указана непосредственно на рисунках, а зависимость
указана непосредственно на рисунках, а зависимость
у = 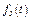 дана в табл. К1 (для рис. 0 - 2 в столбце 2, для рис. 3 - 6 в столбце 3, для
дана в табл. К1 (для рис. 0 - 2 в столбце 2, для рис. 3 - 6 в столбце 3, для
рис. 7 - 9 в столбце 4). Как и в задачах С1 – С2, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 - по последней.
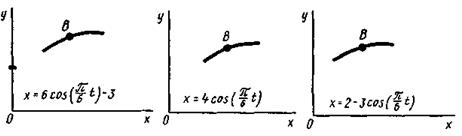
Рис.К1.0 Рис.К1.1 Рис.К1.2
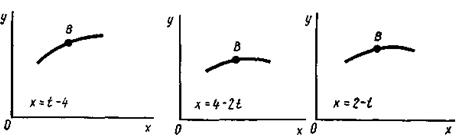
Рис.К1.3 Рис.К1.4 Рис.К1.5
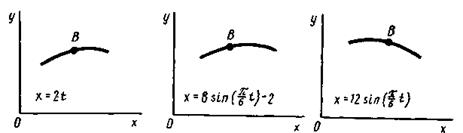
Рис.К1.6 Рис.К1.7 Рис.К1.8
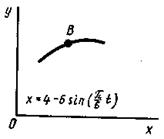
Рис.К1.9
Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону 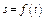 заданному в табл. К1 в столбце 5 (s - в метрах, t - в секундах), где
заданному в табл. К1 в столбце 5 (s - в метрах, t - в секундах), где 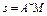 - расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени
- расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени 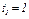 с. Изобразить на рисунке векторы
с. Изобразить на рисунке векторы 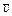 и, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s – от А к М.
и, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s – от А к М.
Указания. Задача К1 относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах (координатный способ задания движения точки), а также формул, по которым определяются скорость, касательное и нормальное ускорение точки при естественном способе задания её движения.
В задаче все искомые величины нужно определить только для момента времени 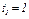 с. В некоторых вариантах задачи K1а при определении траектории или при последующих расчетах (дли их упрощения) следует учесть известные из тригонометрии формулы:
с. В некоторых вариантах задачи K1а при определении траектории или при последующих расчетах (дли их упрощения) следует учесть известные из тригонометрии формулы: 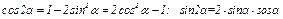
Пример К1а. Даны уравнения движения точки в плоскости ху:
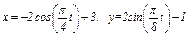 , где (х, у — в сантиметрах, t — в секундах).
, где (х, у — в сантиметрах, t — в секундах).
Определить уравнение траектории точки; для момента времени 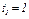 с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
с найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение.
1.Для определений уравнения траектории точки исключим из заданных уравнений движения время t. Поскольку t входит в аргументы тригонометрических функций, где один аргумент вдвое больше другого, используем формулу
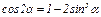 или
или 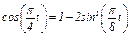 (1)
(1)
Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим
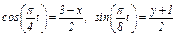 .
.
Следовательно,
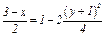
Отсюда окончательно находим следующее уравнение траектории точки (параболы, рис. К1а):
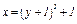 (2)
(2)
2. Скорость точки найдем по её проекциям на координатные оси:
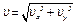 , где
, где 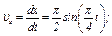
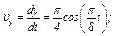
и при 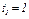 с
с
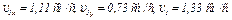 (3)
(3)
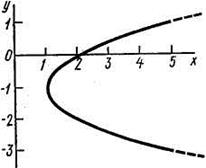
Рис. К1а
3. Аналогично найдем ускорение точки:
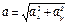 , где
, где 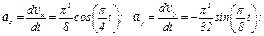
и при 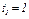 с
с
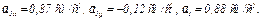 (4)
(4)
4. Касательное ускорение точки найдем, дифференцируя по времени равенство 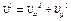 . Получим
. Получим
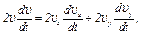
откуда
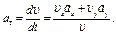 (5)
(5)
Числовые значения всех величин, входящих в правую часть выражения (5), определены и даются равенствами (3) и (4). Подставив в (5) эти числа, найдем сразу, что при 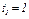 с касательное ускорение точки составит
с касательное ускорение точки составит 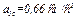 .
.
5. Нормальное ускорение точки 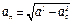 . Подставляя сюда найденные числовые значения
. Подставляя сюда найденные числовые значения 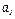 и
и 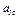 получим, что при
получим, что при 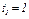 с нормальное ускорение точки составит
с нормальное ускорение точки составит 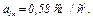
6. Радиус кривизны траектории 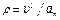 . Подставляя сюда числовые значения
. Подставляя сюда числовые значения 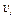 и
и 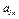 , найдем, что при
, найдем, что при 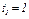 с радиус кривизны составит
с радиус кривизны составит 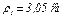 .
.
Ответ: 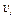 = 1,33 см/с,
= 1,33 см/с, 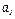 = 0,88 см/с2,
= 0,88 см/с2, 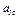 = 0,66 см/с2,
= 0,66 см/с2, 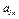 = 0,58 см/с2,
= 0,58 см/с2,
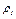 = 3,05 см.
= 3,05 см.
Пример К1б. Точка движется по дуге окружности радиуса R = 2 м по закону 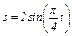 (s - в метрах, t - в секундах), где
(s - в метрах, t - в секундах), где 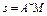 (рис. К1б). Определить скорость и ускорение точки в момент времени
(рис. К1б). Определить скорость и ускорение точки в момент времени 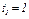 с.
с.
Решение. Определяем скорость точки:
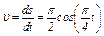 .
.
При 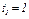 с получим
с получим 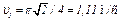
Ускорение находим по его касательной и нормальной составляющим:
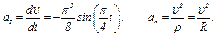
При 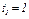 с получим, учтя, что R = 2м,
с получим, учтя, что R = 2м,
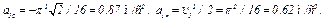
Тогда ускорение точки при 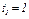 с
с
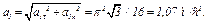
Изобразим на рис. К1б векторы 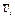 и
и 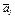 учитывая знаки
учитывая знаки 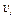 и
и 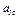 , и считая положительным направление от А к М.
, и считая положительным направление от А к М.
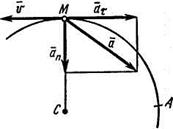
Рис. К1б
Задача К2
Механизм состоит из ступенчатых колес 1 - 3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес (рис. К2.0 - К2.9, табл. К2). Радиусы ступеней колес равны соответственно: у колеса 1 — 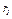 = 2 см,
= 2 см, 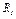 = 4 см, у колеса 2 —
= 4 см, у колеса 2 — 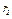 = 6 см,
= 6 см, 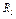 = 8 см, у колеса 3 —
= 8 см, у колеса 3 — 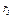 = 12 см,
= 12 см, 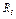 = 16 см. На ободьях колес расположены точки А, В и С.
= 16 см. На ободьях колес расположены точки А, В и С.
В столбце «Дано» таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где 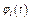 - закон вращения колеса 1,
- закон вращения колеса 1, 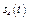 - закон движения рейки 4,
- закон движения рейки 4, 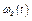 - закон изменения угловой скорости колеса 2,
- закон изменения угловой скорости колеса 2, 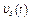 - закон изменения скорости груза 5 и т. д. (везде
- закон изменения скорости груза 5 и т. д. (везде 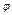 выражено в радианах,
выражено в радианах, 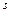 - в сантиметрах,
- в сантиметрах,
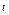 - в секундах). Положительное направление для
- в секундах). Положительное направление для 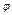 и
и 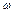 против хода часовой стрелки, для
против хода часовой стрелки, для 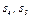 и
и 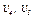 — вниз.
— вниз.
Определить в. момент времени 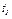 =2 с указанные в таблице в столбцах «Найти» скорости (
=2 с указанные в таблице в столбцах «Найти» скорости (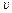 — линейные,
— линейные, 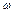 — угловые) и ускорения (
— угловые) и ускорения (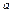 — линейные,
— линейные, 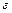 — угловые) соответствующих точек или тел (
— угловые) соответствующих точек или тел (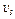 — скорость груза 5 и т.д.).
— скорость груза 5 и т.д.).
Указания. Задача К2 — на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что, когда два колеса находятся в зацеплении, скорость точки зацепления каждого колеса одна и та же, а когда два колеса связаны ременной передачей, то скорости всех точек ремня и, следовательно, точек,
лежащих на ободе каждого из этих колес, в данный момент времени численно одинаковы; при этом считается, что ремень по ободу колеса не скользит.
Таблица К2
| Номер условия | Дано | Найти | |
| скорости | ускорения | ||
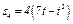
| 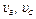
| 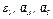
| |
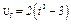
| 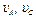
| 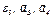
| |
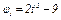
| 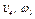
| 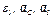
| |
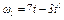
| 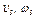
| 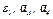
| |
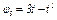
| 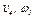
| 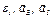
| |
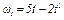
| 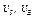
| 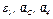
| |
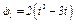
| 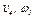
| 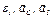
| |
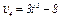
| 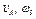
| 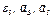
| |
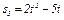
| 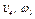
| 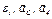
| |
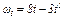
| 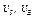
| 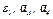
|
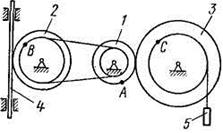
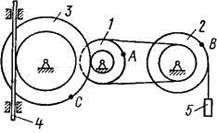
Рис. К2.0 Рис. К2.1
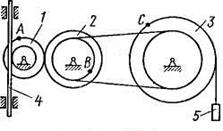
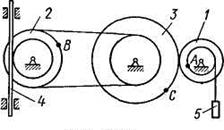
Рис. К2.2 Рис. К2.3
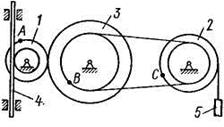
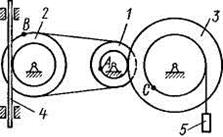
Рис. К2.4 Рис. К2.5
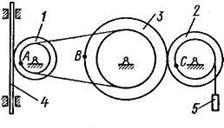
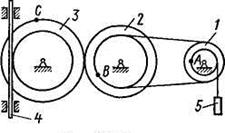
Рис. К2.6 Рис. К2.7
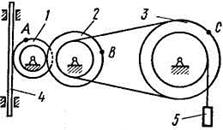
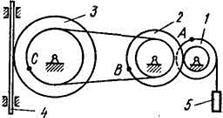
Рис. К2.8 Рис. К2.9
Пример К2. Рейка 1, ступенчатое колесо 2 с радиусами 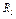 и
и 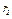 и колесо 3 радиуса
и колесо 3 радиуса 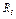 скрепленное с валом радиуса
скрепленное с валом радиуса 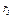 находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К.2). Рейка движется по закону
находятся в зацеплении; на вал намотана нить с грузом 4 на конце (рис. К.2). Рейка движется по закону 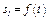 .
.
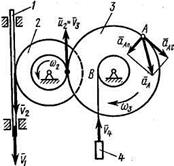
Рис. К2
Дано: 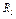 = 6 см,
= 6 см, 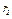 = 4 см,
= 4 см, 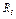 = 8 см,
= 8 см, 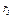 = 3 см,
= 3 см, 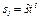 (s — в сантиметрах,
(s — в сантиметрах,
t — в секундах), А - точка обода колеса 3, 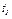 = 3 с.
= 3 с.
Определить: 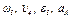 в момент времени
в момент времени 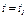
Решение. Условимся обозначать скорости точек, лежащих на внешних ободах колес (радиуса Ri), через 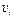 а точек, лежащих на внутренних ободах (радиуса ri), через ui
а точек, лежащих на внутренних ободах (радиуса ri), через ui
1. Определяем сначала угловые скорости всех колес как функции времени t. Зная закон движения рейки 1, находим ее скорость:
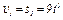 . (1)
. (1)
Так как рейка и колесо 2 находятся в зацеплении, то 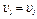 или
или 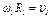 Но колеса 2 и 3 тоже находятся в зацеплении, следовательно,
Но колеса 2 и 3 тоже находятся в зацеплении, следовательно, 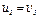 или
или 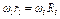 Из этих равенств находим
Из этих равенств находим
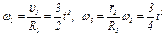 (2)
(2)
Тогда для момента времени 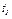 = 3 с получим
= 3 с получим 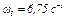
2. Определяем 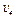 . Так как
. Так как 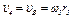 то при
то при 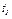 = 3 с скорость
= 3 с скорость 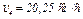 .
.
3. Определяем 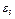 . Учитывая второе из равенств (2), получим
. Учитывая второе из равенств (2), получим 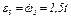 . Тогда при
. Тогда при 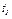 = 3 с угловое ускорение
= 3 с угловое ускорение 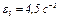
4. Определяем 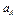 . Для точки А:
. Для точки А: 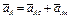 где численно
где численно 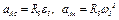 . Тогда для момента времени
. Тогда для момента времени 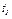 = 3 с имеем
= 3 с имеем
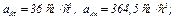
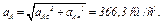
Все скорости и ускорения точек, а также направления угловых скоростей показаны на рис. К2.
Ответ: 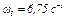 ;
; 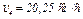 ;
; 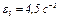 ;
; 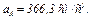
Задача К3
Плоский механизм состоит из стержней 1, 2, 3, 4 иползуна В или Е
(рис. К3.0 - К3.7) или из стержней 1, 2, 3 иползунов В и Е (рис. К3.8, КЗ.9), соединенных друг с другом и с неподвижными опорами О1, О2 шарнирами; точка D находится в середине стержня АВ. Длины стержней равны соответственно l1= 0,4 м, l2= 1,2 м,
l3= 1,4 м, l4= 0,6 м. Положение механизма определяется углами 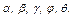 Значения этих углов и других заданных величин указаны в табл. К3а (для рис. 0 - 4) или в табл. К3б (для рис. 5 - 9); при этом в табл. К3а
Значения этих углов и других заданных величин указаны в табл. К3а (для рис. 0 - 4) или в табл. К3б (для рис. 5 - 9); при этом в табл. К3а 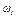 и
и 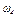 - величины постоянные.
- величины постоянные.
Определить величины, указанные в таблицах в столбцах «Найти».
Дуговые стрелки на рисунках показывают, как при построении чертежа механизма должны откладываться соответствующие углы: по ходу или против хода часовой стрелки (например, угол 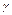 на рис. 8 следует отложить от DB по ходу часовой стрелки, а на рис. 9 — против хода часовой стрелки и т.д.).
на рис. 8 следует отложить от DB по ходу часовой стрелки, а на рис. 9 — против хода часовой стрелки и т.д.).
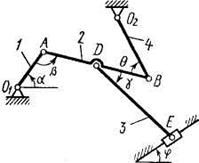
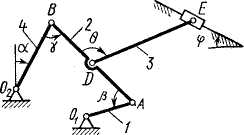
Рис. К3.0 Рис. К3.1
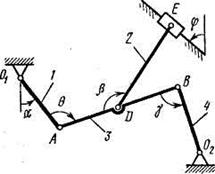
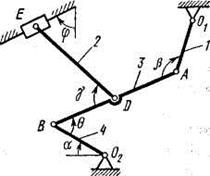
Рис. К3.2 Рис. К3.3
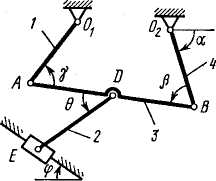
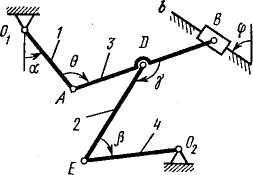
Рис. К3.4 Рис. К3.5
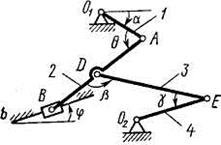
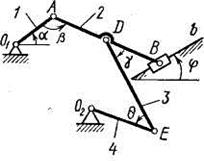
Рис. К3.6 Рис. К3.7
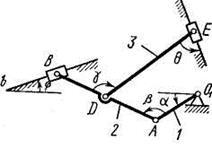
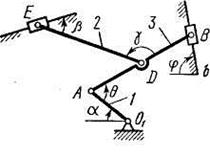
Рис. К3.8 Рис. К3.9
Построение чертежа начинать со стержня, направление которого определяется углом a; ползун с направляющими для большей наглядности изобразить так, как в примере К3 (см. рис. К3б).
Заданные угловую скорость и угловое ускорение считать направленными против часовой стрелки, а заданные скорость 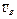 и ускорение
и ускорение 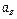 — от точки В к b (на рис. 5 - 9).
— от точки В к b (на рис. 5 - 9).
Таблица К3а (к рис. К3.0 — К3.4)
| Номер условия | Углы, град | Дано | Найти | ||||||||
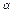
| 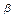
| 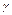
| 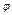
| 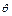
| 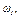 с-1
с-1
| 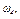 с-1
с-1
| 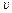 точек
точек
| 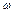 звена
звена
| 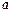 точки
точки
| 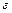 звена
звена
| |
| – | В, Е | DE | B | AB | |||||||
| – | А, Е | AB | A | AB | |||||||
| – | В, Е | AB | B | AB | |||||||
| – | А, Е | DE | A | AB | |||||||
| – | D, Е | AB | B | AB | |||||||
| – | А, Е | AB | A | AB | |||||||
| – | В, Е | DE | B | AB | |||||||
| – | А, Е | DE | A | AB | |||||||
| – | D, Е | AB | B | AB | |||||||
| – | А, Е | DE | A | AB |
Таблица К3б (к рис. К3.5 — К3.9)