Проверить справедливость теоремы Коши для следующих пар функций. Найти с.

Основные теоремы дифференциального исчисления

Справочный материал

I. Теоремы о средних значениях

Теорема Ферма. Если функция y=f(x) удовлетворяет условиям:

1⁰ дифференцируема в интервале (a;b)

2⁰ достигает наибольшего (наименьшего) значения во внутренней точке х ₀Î(a;b).

Тогда f ¢(x ₀)=0.

 

Геометрический смысл: В точке х ₀, удовлетворяющей условиям теоремы, касательная к графику y=f(x) параллельна Ох.

Замечание: Если нарушается хотя бы одно из условий теоремы, то производная f ¢(x ₀) может и не быть нулем. Например, в точке экстремумапроизводная может вообще не существовать.

 

Теорема Ролля. Если функция y=f(x) удовлетворяет условиям:

1⁰ непрерывна на [ a;b ]

2⁰ дифференцируема в (a;b)

3⁰ f(a)=f(b)

Геометрический смысл: Если крайние ординаты графика дифференцируемой функции равны, то на кривой найдётся хотя бы одна точка, в которой касательная параллельна Ох.

Тогда $ с Î(a;b): f ¢(c)=0.

 

 

Теорема Коши (об отношении приращений двух функций). Если функции y=f(x) и y=j (x) удовлетворяют условиям:

1⁰ непрерывны на [ a;b ]

2⁰ дифференцируемы в (a;b)

3⁰ j ¢(x)¹0, " х Î(a;b)

Тогда $ с Î(a;b): .

 

Теорема Лагранжа (о конечном приращении). Если функция y=f(x) удовлетворяет условиям:

1⁰ непрерывна на [ a;b ]

2⁰ дифференцируема в (a;b)

Геометрический смысл: На кривой графика дифференцируемой функции найдётся точка, касательная в которой параллельна хорде, стягивающей концы дуги .

Тогда $ с Î(a;b): f (b) - f (a)= f¢ (c)×(b-a).

 

 

II. Раскрытие неопределенностей с помощью правила Лопиталя

Правило Лопиталя. Пусть функции f(x) и j(x) дифференцируемы в некоторой окрестности точки х ₀ и j ¢(x)¹0, " х ÎO_d(х ₀), (x ¹ x ₀). Тогда, если f(x) = j (x) =0 ( f (x)= j (x)=¥) и существует , то

- предел отношения б.м.ф. (б.б.ф.) равен пределу отношения их производных, если последний существует.

 

Замечания:

1. Теорема Лопиталя применима, если имеет место неопределенность [0/0], [¥/¥] при х®х₀. Теорема верна и в случае, когда х®¥.

2. Если производные f¢(x) и j¢(x) удовлетворяют условиям теоремы (отношение представляет неопределённость [0/0], [¥/¥]), то теорему можно применить второй раз: = = и т.д.

 

Неопределенности [0×¥], [¥ - ¥]. С помощью алгебраических преобразований приводятся к виду [0/0], [¥/¥].

Неопределенности [1^¥], [¥⁰], [0⁰]. С помощью логарифмирования приводятся к виду [0×¥]. При этом используется соотношение, основанное на свойствах логарифмов и непрерывности показательной функции

Задачи

1. Проверить, удовлетворяет ли функция f(x) на данном отрезке условиям теоремы Ферма. Найти соответствующее значение х ₀, если оно существует

.

 

Выявить нарушение условий теоремы Ролля, для функций представленных на рисунке

y=x2

y=|x|

 

3. Проверить справедливость теоремы Ролля для функции f(x) на данном отрезке. Найти соответствующее значение с, если оно существует

.

 

4. Проверить справедливость теоремы Лагранжа для функции f (x) на данном отрезке. Найти соответствующее значение с (если оно существует). Сделать графическую иллюстрацию.

 

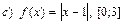
5. Найти точку, в которой касательная к кривой у = f (x) параллельна хорде, стягивающей точки А и В этой кривой.

.

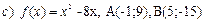Проверить справедливость теоремы Коши для следующих пар функций. Найти с.

.

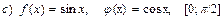
7^*. Доказать тождества

.