Основная часть
Хорошо известно, что высший аналог второго уравнения Пенлеве [5]
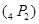
имеет преобразование Беклунда и обратное к нему, определяемые формулами
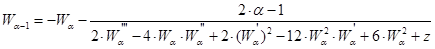, (1)
, (2)
соответственно с произвольным параметром 
.
Это означает, что если известно решение уравнения
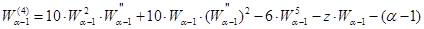(3)
при некотором фиксированном значении параметра , то формула (2) позволяет получить решение уравнения 
при фиксированном значении параметра .
И наоборот, если известно решение уравнения при фиксированном значении параметра , то с помощью (1) можно получить решение уравнения (3).
При этом предполагается, что знаменатели дробей в (1) и (2) при любых значениях z отличны от нуля.
Система (1), (2) эквивалентна по 
уравнению:
, (4)
где
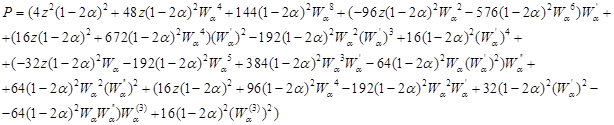
Относительно 
система (1), (2) также эквивалентна уравнению шестого порядка
, (5)
где
Нетрудно проверить, что уравнение (5) получается из (4) с помощью преобразований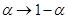 
, 
.
Справедливо следующее утверждение.
Теорема 1. Все решения уравнения являются одновременно решениями уравнения (4).
В справедливости данной теоремы можно убедиться, если из 
найти 
, 
и вместе с 
подставить в уравнение (4).
Остановимся на некоторых свойствах решений уравнения . Лемма. Уравнение можно записать в виде системы
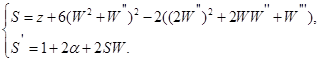(6)
Справедливость этого утверждения устанавливается исключением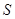 
из системы (6).
Заметим, что из (6) также следует существование трёхпараметрического семейства решений уравнения при 
, которое определяется общим решением уравнения
(7)
Действительно, если в (6) положить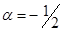 
, 
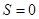, то мы получаем уравнение (7).
Для интегрирования уравнения (7) введём функцию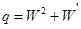 
. Тогда 
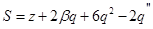и система (6) перепишется в виде
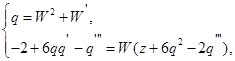(8)
а уравнение (7) - в виде
. (9)
Ясно, что уравнение (9) интегрируется посредством первого трансцендентна Пенлеве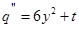 
заменой 
, 
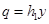, где 
, 
. Таким образом, справедлива [5]
Теорема 2. Произвольное решение уравнения Риккати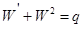 
, где q - произвольное решение первого уравнения Пенлеве, является решением уравнения 
.
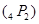Известно также [5], что уравнение 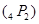имеет рациональные решения тогда и только тогда, когда 
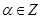. Они легко получаются из тривиального решения 
при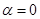 
с помощью формул (1), (2). В частности, при 
имеем решение 
, а при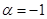 
решение 
.
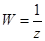Характерной особенностью уравнения 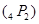является то, что оно является частным случаем уравнения
, 
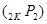
где 
, 
, 
,
получающегося из высшей иерархии 
Кортевега де Фриза
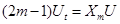, (10)
где 
, 
, 
при помощи редукции
, 
.
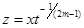При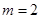 
уравнения 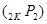и (10) являются [6] классическими уравнениями Кортевега де Фриза и вторым уравнением Пенлеве связанными преобразованием
, 
.
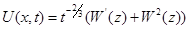Для 
в 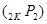получаем уравнение 
. Ещё одной важной особенностью уравнения является то, что оно имеет трёхпараметрические и двухпараметрические семейства полярных решений [7]. В силу теоремы 1 таким же свойством обладает и уравнение (5).
Подробное описание различных свойств решений уравнения 
в связи с их многочисленными приложениями содержится в учебном пособии [8].
Заключение
Исследование аналитических свойств решений системы двух нелинейных дифференциальных уравнений третьего порядка, порождаемой прямым и обратным преобразованиями Беклунда высшего аналога второго уравнения Пенлеве позволило доказать существование у неё четырёхпараметрического семейства решений, порождаемого общим решением высшего аналога второго уравнения Пенлеве. На основании этого доказано существование у системы рациональных, а также двух - и трёхпараметрических семейств полярных решений. Работа (в рамках поставленной задачи) является завершённой.
В процессе исследований использовался пакет символьных вычислений МАТЕМАТИКА.
Список использованных источников
1. Абловиц М., Сигур Х. Солитоны и метод обратной задачи. - М.: Мир. 1987. - 479 с.
2. Ньюэлл А. Солитоны в математике и физике. - М.: Мир. 1989. - 328 с.
3. Калоджеро Ф., Дегасперис А. Спектральные преобразования и солитоны. - М.: Мир. 1985. - 472 с.
4. Баренблатт Г.И. Подобие, автомодельность, промежуточная асимптотика. - Л.: 1982. - 255 с.
5. Gromak V.I. Backlund transformations of Painleve’ equations and their applications // The Painleve’ property, one century later. CRM series in Mathematical Physics /. Ed. R. Conte. - New York: Springer-Verlag, 1999. - P.687-734.
6. Airault H. Rational solutions of Painleve’ equations // Stud. Appl. Math. - 1979. - Vol.61. - P.31-53.
7. Громак В.И., Голубева Л.Л. Обобщённое второе управление Пенлеве четвертого порядка // Весцi НАН Беларусi. Серыя фiз. - мат. Навук. - 2004 (в печати).
8. Кудряшов Н.А. Аналитическая теория нелинейных дифференциальных уравнений. - М. 2002. - 304 с.