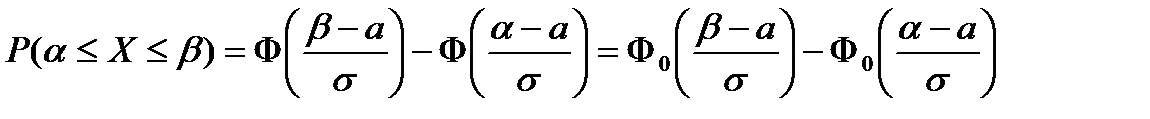ОСНОВНЫЕ ФОРМУЛЫПО ТЕОРИИ ВЕРОЯТНОСТЕЙ (часть 1)
| Элементы комбинаторики | ||
Число размещений без повторений (выборка отличается одна от другой либосоставомэлементов, либо порядком их расположения)
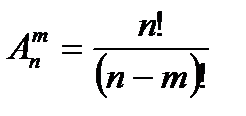 , 0!=1, 1!=1, 2!=2, 3!=6, 4!=24, 5!=120, 6!=720 , 0!=1, 1!=1, 2!=2, 3!=6, 4!=24, 5!=120, 6!=720
| Число сочетаний без повторений (одно размещение отличается от другого хотя бы одним элементом (только составом))
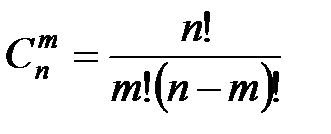 , ,
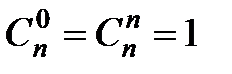 , , 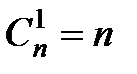
| Число перестановок без повторений (одно размещение отличается от другого только порядком расположения элементов)
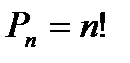
|
Число размещений с повторениями
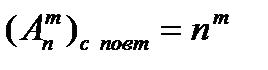
| Число сочетаний с повторениями
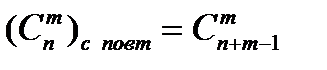
| Число перестановок с повторениями
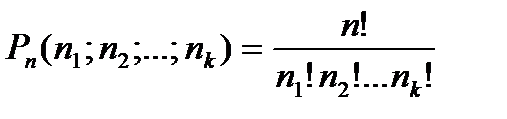 , где , где 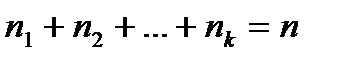
|
Вероятность события 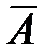 , противоположного событию , противоположного событию 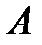
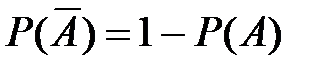 Þ Þ 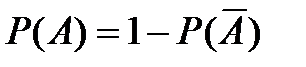
| Классическая вероятность
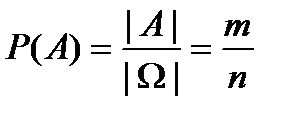
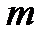 - число исходов, благоприятствующих событию, - число исходов, благоприятствующих событию, 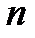 - число всевозможных исходов - число всевозможных исходов
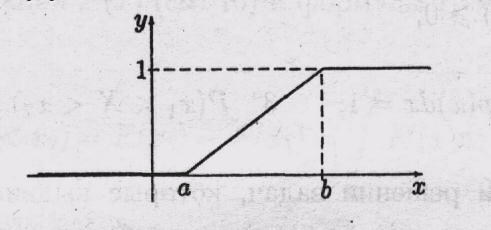
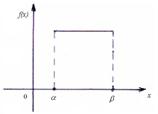
| Геометрическая вероятность
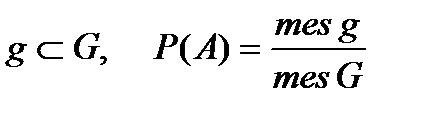
|
| Вероятность суммы | |
а) для произвольных событий
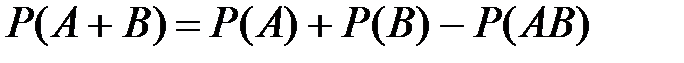 ; ;
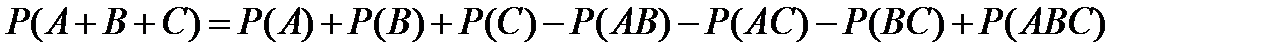
| б) для несовместных событий 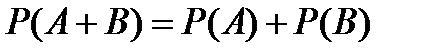
|
| Вероятность произведения | |
а) для произвольных событий A и B: 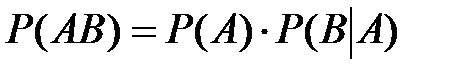
| б) если события A и В независимы: 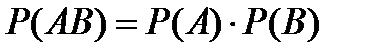
|
Формула полной вероятности
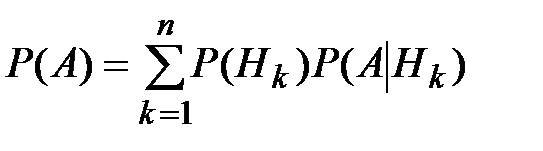
| Формулы Бейеса
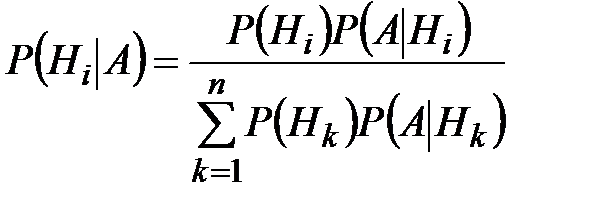
| Формула Бернулли
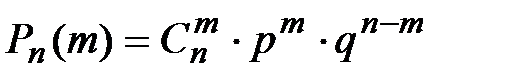 , ,

|
Наивероятнейшее число 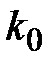 появлений события в независимых испытаниях
np-q ≤ k 0 ≤ np+p
1)если число np+p - дробное, то имеем одно наивероятнейшее число k 0=[ np+p ],
2)если np+p -целое, то имеем два наивероятнейших числа: k 0 = np-q и k 0= np+p появлений события в независимых испытаниях
np-q ≤ k 0 ≤ np+p
1)если число np+p - дробное, то имеем одно наивероятнейшее число k 0=[ np+p ],
2)если np+p -целое, то имеем два наивероятнейших числа: k 0 = np-q и k 0= np+p
| Формула Пуассона
(редких событий)
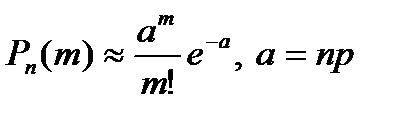 (обычно при n≥5, a=np≤10)
(обычно при n≥5, a=np≤10)
| Вероятность появления m событий простейшего потока за время t
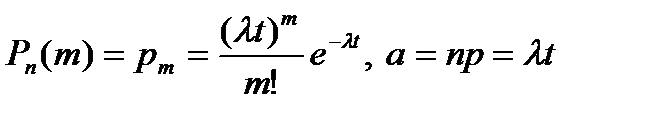
|
Локальная теорема Муавра-Лапласа
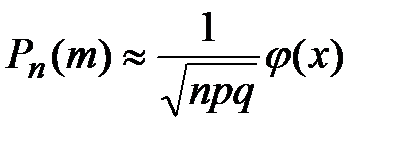 , где , где 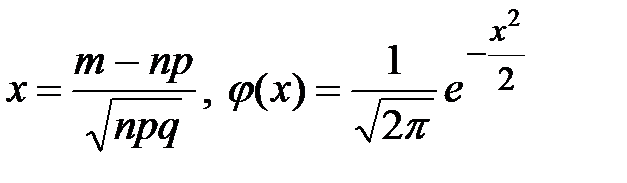 (когда число испытаний n велико, а вероятность p наступления события не близка к 0 (обычно npq³10))
(когда число испытаний n велико, а вероятность p наступления события не близка к 0 (обычно npq³10))
| Функция Лапласа
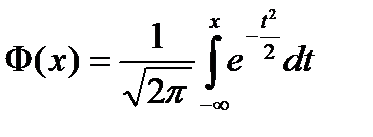 Нормированная
функция Лапласа
Нормированная
функция Лапласа
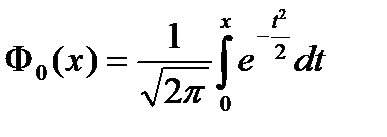
| Свойства нормированной функции Лапласа:
1)Нечётность 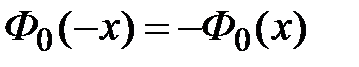 ;
2)Монотонно возрастающая Ф0 (х);
3) ;
2)Монотонно возрастающая Ф0 (х);
3) 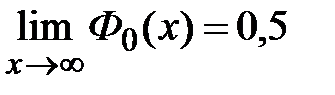 Ф0 (0)=0.
На практике: если х ³5, полагаем что Ф0(х)»1/2 Ф0 (0)=0.
На практике: если х ³5, полагаем что Ф0(х)»1/2
|
Интегральная теорема Муавра-Лапласа
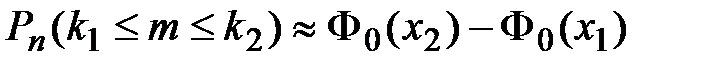 , где , где 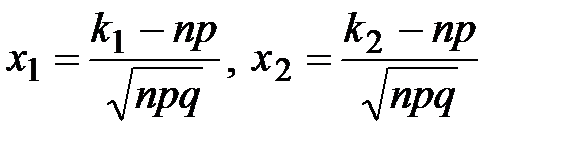 (обычно npq³20)
(обычно npq³20)
| Отклонение относительной частоты от постоянной вероятности в n независимых испытаниях
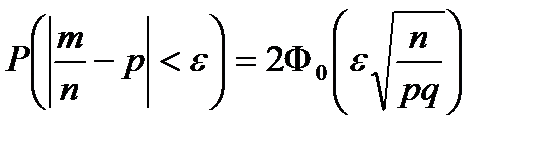
|
ОСНОВНЫЕ ФОРМУЛЫПО ТЕОРИИ ВЕРОЯТНОСТЕЙ (часть 2)
| Дискретная с.в. X | Абсолютно-непрерывная с.в. X | ||||||||||
1) Задан закон распределения
pi ≥0 и p 1+ p 2+…+ pk =1
| 1) Задана плотность распределения p (x) (или f (x)):
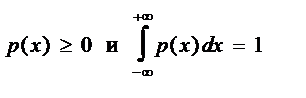
| ||||||||||
| 2) Функция распределения (интегральный закон распределения): F (x)= P (X < x) | |||||||||||
3) Свойства функции распределения F (x):
а) 0≤ F (x)≤1;
б) F (x) – монотонно возрастающая;
в) 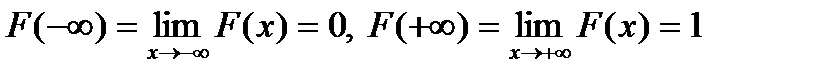 ;
г) F (x) – непрерывна слева ;
г) F (x) – непрерывна слева
| |||||||||||
4) 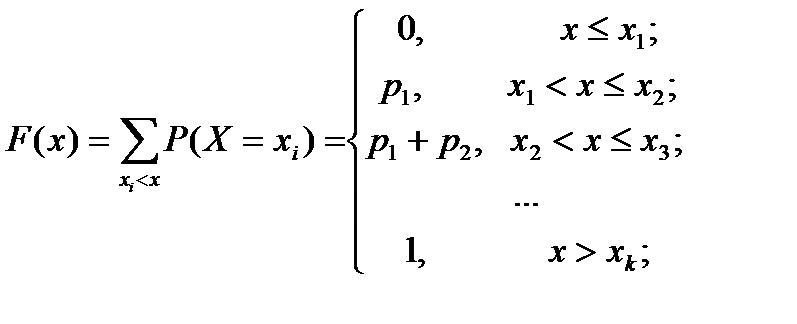
| 4) 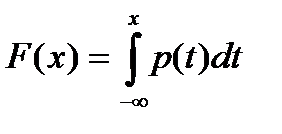 , , 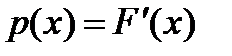
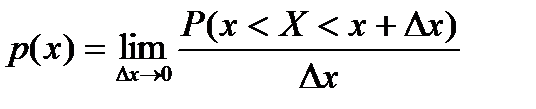
| ||||||||||
5) 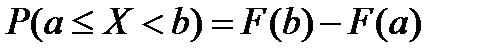 ; ; 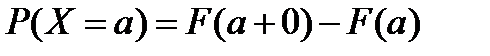
| |||||||||||
6) 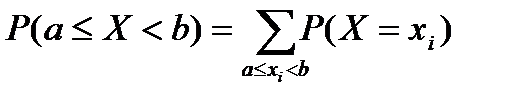 ; ; 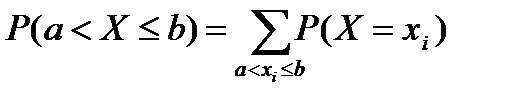 ; ;
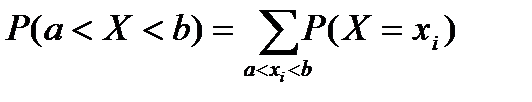 ; ; 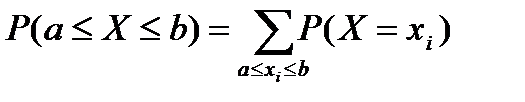 ; ;
| 6) 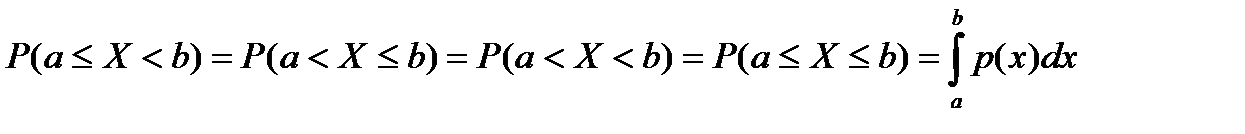
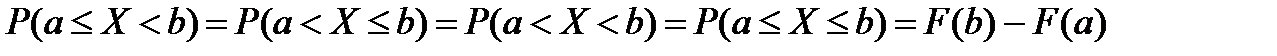
| ||||||||||
| Числовые характеристики Математическое ожидание (среднее значение) M(X): | |||||||||||
7) 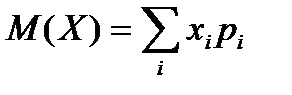 ; ; 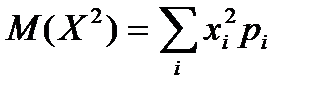
| 7) 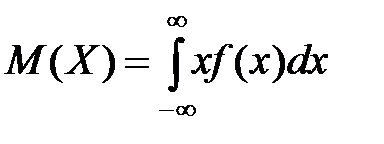 ; ; 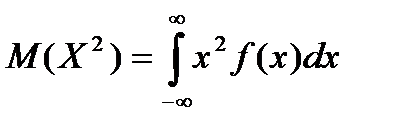
| ||||||||||
| 8) Свойства M(X): 1. M(C)=C (C-const); 2. M(CX)=CM(X) (C-const); 3. M(X±Y)=M(X)±M(Y); 4. M(X·Y)=M(X)·M(Y), если X, Y – независимые с.в. 5. X≥YÞM(X)≥M(Y) | |||||||||||
| 9) Дисперсия: D(X)=M[(X-M(X))2]; D(X)=M(X2)-(M(X))2 | |||||||||||
10) 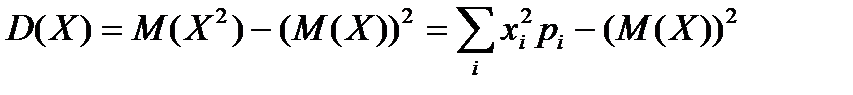
| 10) 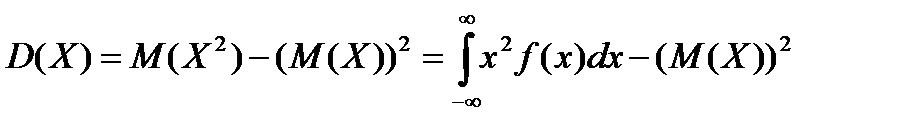
| ||||||||||
| 11) Свойства D(X): 1. D(X)≥0 2. D(C)=0 (C-const); 3. D(CX)=C2D(X) (C-const); 4. D(X±Y)=D(X)+D(Y), если X, Y – независимые с.в.; | |||||||||||
12) среднее квадратическое отклонение 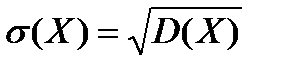
| |||||||||||
| 13) Начальный момент s-го порядка с.в.X: ms(X)=M(Xs) | |||||||||||
| 14) Центральный момент порядка s с.в.X: ms(X)=M[(X-M(X))s] а) m2(X)=m2(X)-m12(X) б) m3(X)=m3(X)-3m1(X)m2(X)+2m13(X) в) m4(X)=m4(X)-4m1(X)m3(X)+6m12(X)m2(X)-3m14(X) | |||||||||||
15) Коэффициент асимметрии с.в.X: 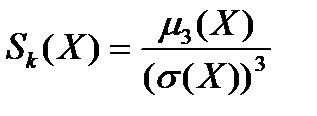
| |||||||||||
16) Коэффициент эксцесса с.в X: 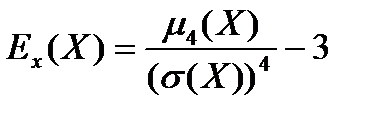
| |||||||||||
| 17) Ковариация с.в. x1 и x2:cov(x1, x2)=M[(x1 -Mx1)·(x2 -Mx2)]; cov(x1, x2)=M(x1·x2)-Mx1 ·Mx2; | |||||||||||
18) Коэффициент корреляции с.в. x1 и x2: 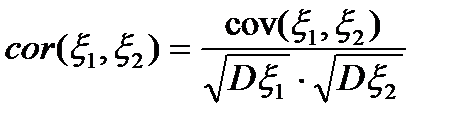
| |||||||||||
ОСНОВНЫЕ РАСПРЕДЕЛЕНИЯ В ТЕОРИИ ВЕРОЯТНОСТЕЙ (часть 3)
| Дискретные с.в. | 1) Биномиальное распределение X~B(n;p)
p – вероятность появления события А в каждом из n независимых испытаний, q= 1 -p
с.в. Х – число появлений события А в серии из n независимых испытаний, Х=0,1,2,…, m,…, n
P(X=m)=Pп(m)= 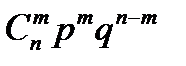 . Закон распределения с.в.X: . Закон распределения с.в.X:
М(Х)=np; D(X)=npq; σ(X)= | ||||||||||||||
2) Пуассоновское распределение X~П a
p – вероятность появления события А в каждом из n независимых испытаний, q= 1 -p (случай, когда n достаточно большое, а p – достаточно малое). Пусть a=np – параметр распределения Пуассона.
с.в. Х – число появлений события А в серии независимых испытаний, Х=0,1,2,…, m,… P(X=m)=Pп(m)= М (Х) =a; D (Х) =a; σ(Х)= | |||||||||||||||
3) Геометрическое распределение X~G(p)
С.в. X= m, имеющая геометрическое распределение, представляет собой число m испытаний, проведённых по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода, X=1,2,…, m,…., q =1- p P(X= m)= qm-1p. Закон распределения с.в.X:
| |||||||||||||||
| Абсолютно-непрерывные с.в. | 4)
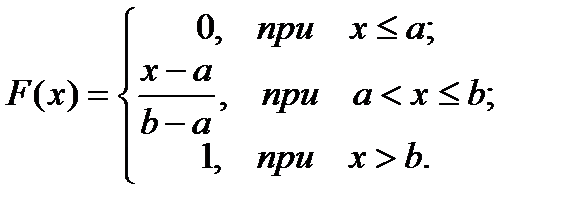 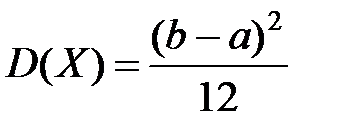
| ||||||||||||||
5) Показательное распределение X~Eλ
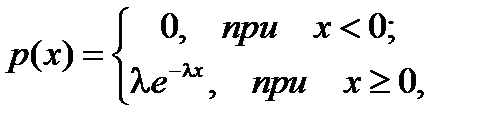 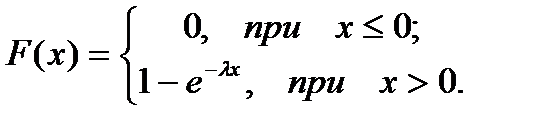 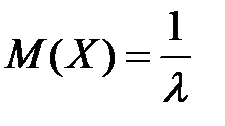 , , 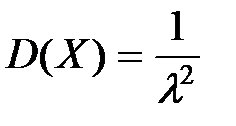

| |||||||||||||||
6) Нормальное распределение X~N(a,s2)
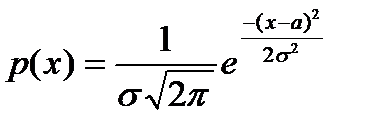 ; ; 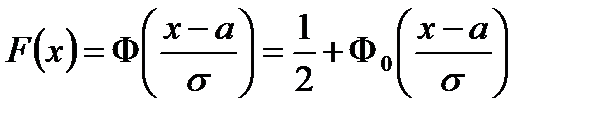 ; ; 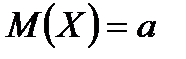 ; ; 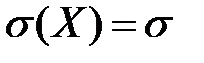 ; ; 
Правило трёх сигм: |
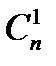 pqn-1
pqn-1
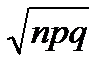
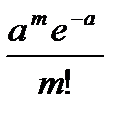 . Закон распределения с.в.X:
. Закон распределения с.в.X: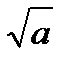
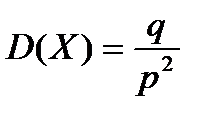
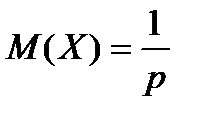
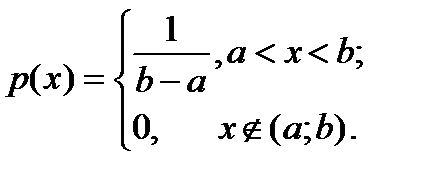
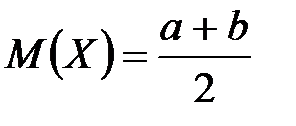 ;
;