Свойства
18.1.2.2. Если сходится ряд (18.2.1), то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
18.1.2.3. Если ряд сходится, то сумма его остатка после n -го члена стремится к нулю при 
18.1.2.4. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.
18.1.2.5. Два сходящихся ряда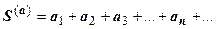 
и 
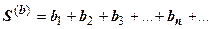можно почленно складывать и вычитать; ряд 
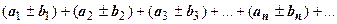также сходится, и его сумма равна 
.
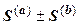18.1.3. Сходимость рядов с положительными членами (положительных рядов). Термином "положительный ряд" мы будем называть числовой ряд с неотрицательными членами: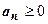 
для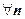 
. Для таких рядов частичная сумма 
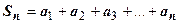является возрастающей функцией аргумента n.
Положительный ряд сходится тогда и только тогда, когда последовательность его частичных сумм ограничена.
18.1.3.1.1. Признак сравнения. Пусть даны два положительных ряда 
и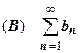 
, для которых, хотя бы начиная с некоторого места (при n > N), выполняется неравенство 
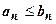. Тогда:
если сходится ряд (В), то сходится ряд (А); если расходится ряд (А), то расходится ряд (В).
18.1.3.1.2. Предельная форма признака сравнения. Если существует конечный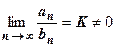 
, то ряды (А) и (В) сходятся или расходятся одновременно.
18.1.3.2.Признак сходимости Коши (радикальный). Пусть для положительного ряда существует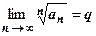 
. Тогда
если q <1, то ряд сходится,
если q >1, то ряд расходится,
если q =1, то ряд может и сходиться, и расходиться.
18.1.3.3.Признак сходимости Даламбера. Пусть для положительного ряда существует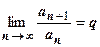 
. Тогда
если q <1, то ряд сходится,
если q >1, то ряд расходится,
если q =1, то ряд может и сходиться, и расходиться.
Интегральный признак коши Теорема. Пусть члены положительного числового ряда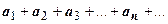 
являются значениями непрерывной монотонно убывающей неотрицательной функции 
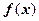при натуральных значениях аргумента: 
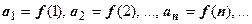Тогда ряд 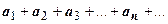и 
несобственный интеграл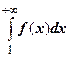 
сходятся или расходятся одновременно.
18.1.4. Знакопеременные ряды. Так мы будем называть ряды, которые содержат бесконечные множества как положительных, так и отрицательных членов.
Определение. Ряд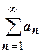 
называется абсолютно сходящимся, если сходится ряд 
абсолютных величин его членов. Если ряд 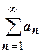сходится, а ряд расходится, то ряд 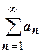называется условно сходящимся.
Достаточный признак сходимости знакочередующегося ряда (признак Лейбница). Если
1. Последовательность, составленная из модулей членов знакочередующегося ряда, монотонно убывает, т.е.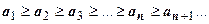 
;
2. Выполняется необходимый признак сходимости ряда, т.е.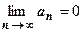 
,
то ряд сходится.
18.1.5.1. Необходимый признак сходимости ряда. Общий член сходящегося ряда стремится к нулю: .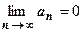
18.1.5.2. Если сходится ряд, то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.
18.1.5.3. Если ряд сходится, то сумма его остатка после n -го члена стремится к нулю при .
18.1.5.4. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.
18.1.5.5. Два сходящихся ряда можно почленно складывать и вычитать, полученный ряд также сходится, и его сумма равна, соответственно, сумме или разности исходных рядов.
18.1.5.6. Сочетательное свойство сходящегося ряда. Если члены сходящегося ряда 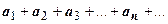сгруппировать произвольным образом: 
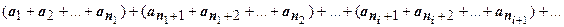(здесь 
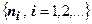- строго возрастающая последовательность натуральных чисел), и составить новый ряд из сумм членов в каждой паре круглых скобок, то этот новый ряд тоже будет сходиться, и его сумма будет равна сумме исходного ряда.