(среднее значение, дисперсия, среднеквадратическое
отклонение, коэффициент вариации)
Основными числовыми характеристиками распределения износа являются: среднее значение, среднее квадратическое отклонение и коэффициент вариации.
Среднее значение определяется по формуле [3]:
 , (1.2.12)
, (1.2.12)
где  – среднее значение;
– среднее значение;
 – середина i -го интервала;
– середина i -го интервала;
 – опытная вероятность в i -м интервале;
– опытная вероятность в i -м интервале;
n – число интервалов статистического ряда.
Расчет числовых характеристик удобно выполнять в табличной форме. Для этого на основе статистического ряда составляется вспомогательная табл. 1.2.5. В эту таблицу переносятся из статистического ряда столбцы i, hci и pi. Справа таблица дополняется еще двумя столбцами, в которые записываются вспомогательные величины G 1 и G 2 – произведения, стоящие под знаком суммы в формулах (1.2.12) и (1.2.13):
 ,
,
 .
.
После заполнения столбца  и вычисления его суммы получаем среднее значение износа шатунной шейки коленчатого вала
и вычисления его суммы получаем среднее значение износа шатунной шейки коленчатого вала
 = 16,125
= 16,125
Сумма по столбцу  составляет 6,984.
составляет 6,984.
Несмещенная оценка для среднего квадратического отклонения вычисляется по формуле
 =2,683 (1.2.13)
=2,683 (1.2.13)
где σ – среднее квадратическое отклонение;
 – среднее значение;
– среднее значение;
 – середина i -го интервала;
– середина i -го интервала;
 – опытная вероятность в i -м интервале;
– опытная вероятность в i -м интервале;
n – число интервалов статистического ряда;
N – объем выборки.
Таблица 1.1.4
Расчет числовых характеристик распределения износа шатунной шейки коленчатого вала
| Номер интервала | Середина интервала | Опытная вероятность (частость) | 
| 
|
| i | 
| 
| 
| 
|
| 0,28125 | 3,65625 | 2,74658 | ||
| 0,21875 | 3,28125 | 0,27685 | ||
| 0,28125 | 4,78125 | 0,21533 | ||
| 0,09375 | 1,78125 | 0,77490 | ||
| 0,125 | 2,625 | 2,97070 | ||
| Сумма: | 16,125 | 6,984 |
Коэффициент вариации находим по формуле:
 = 0,1663 (1.2.14)
= 0,1663 (1.2.14)
где  – коэффициент вариации;
– коэффициент вариации;
σ – среднеквадратическое отклонение;
2.ПРОВЕРКА ОПЫТНЫХ ДАННЫХ
НА НАЛИЧИЕ ВЫПАДАЮЩИХ ТОЧЕК.
ПОСТРОЕНИЕ ГИСТОГРАММ И ПОЛИГОНА
ОПЫТНОГО РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. ВЫБОР ТЕОРЕТИЧЕСКОГО ЗАКОНА РАСПРЕДЕЛЕНИЯ
Проверка опытных данных на наличие выпадающих точек.
Представленные расчеты являются логическим продолжением формирования общей методики определения статистических параметров.
Проверку опытной информации на наличие выпадающих точек осуществляем по формуле [5]:
 , (1.3.1)
, (1.3.1)
где hi и hi –1 – смежные точки в вариационном ряду износов.
Для наименьшего значения износа шатунной шейки коленчатого вала
h 1 = 13; h 2 = 14.
=  =0,373.
=0,373.
Для наибольшего значения износа гильзы h 32 = 22; h 31 = 22.
= 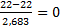 .
.
Построение гистограммы и полигона опытного
распределения случайной величины
По данным статистического ряда можно построить гистограмму и полигон распределения.
Гистограмму строят для распределений непрерывных случайных величин, а полигон – для дискретных, хотя такое правило не является обязательным.
Гистограмма распределения строится следующим образом. На оси абсцисс откладываются границы интервалов.
Из начала каждого интервала проводится ордината высотой, равной частоте для данного интервала, в принятом для оси Y масштабе. Из этой точки проводится горизонтальная линия на всю ширину интервала.
Для построения полигона распределения из середины каждого интервала проводим ординату высотой, равной частоте для данного интервала. Вершины полученных ординат соединяем ломаной линией. Гистограмма и полигон распределения износов гильзы изображены на рисунке 1.3.1, износов поршневого пальца – на рисунке 1.3.2.

Рис. 1.3.1, а. Гистограмма распределения износа гильзы

Рис. 1.3.1, б. Полигон распределения износа гильзы
Полигон или гистограмма позволяют визуально оценить данное распределение и сделать предварительные предположения относительно вида теоретического закона распределения, подходящего к нашим опытным данным.
Распределение износов гильзы (рис. 1.3.1) имеет явно выраженную левостороннюю асимметрию, в то время как распределение износов поршневого пальца (рис. 1.3.2) более или менее симметрично.
Закон нормального распределения (ЗНР)
Формулы дифференциальной и интегральной функций для ЗНР имеют вид:
 , (1.3.2)
, (1.3.2)
 . (1.3.3)
. (1.3.3)
ЗНР – уникальный случай, когда две первые числовые характеристики совпадают с параметрами закона распределения. Поэтому параметры ЗНР для рассматриваемых примеров уже определены и составляют:
– для износов шатунной шейки коленчатого вала
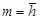 = 16,125мм / 100 ≈ 0,161 мм;
= 16,125мм / 100 ≈ 0,161 мм;
Σ = 2,683 мм / 100 ≈ 0,026 мм;
 (текущее значение износа);
(текущее значение износа);
Закон распределения Вейбулла (ЗРВ)
Формулы дифференциальной и интегральной функций для ЗРВ имеют вид:
 , (1.3.4)
, (1.3.4)
 , (1.3.5)
, (1.3.5)
где а – масштабный параметр;
b – параметр формы;
с – параметр смещения (сдвига).
Следует найти вспомогательную величину Vc по формуле [3]
 =
=  =0,6504 (1.3.6)
=0,6504 (1.3.6)
где σ – среднеквадратическое отклонение;
m – математическое ожидание (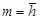 );
);
с – параметр смещения.
Находим параметр b и коэффициент Ка:
– для износов шатунной шейки коленчатого вала
b = 1,573; Ка = 1,114;
Далее с использованием найденного коэффициента Ка находим параметр а по формуле:
 . (1.3.7)
. (1.3.7)
Для износов шатунной шейки коленчатого вала
а = (16,125-12)·1,114 = 4,5952;