Виды сетевых моделей. Задача управления запасами. Воздействие возмущений на критерий качества и на множество допустимых управлений
Планирование и оперативное управление как типичный для экономики способ реализации -общей идеи обратной связи. Многошаговые процедуры управления. Обработка текущей информации о возмущениях, адаптация модели.
Многошаговые схемы управления. Выделение этапов, различающихся составом управленческих решений и информацией о возмущениях. Рекурсивное решение -последовательное применение принципа наилучшего гарантированного результата от заключительного по времени этапа к первому.
Аналитическое решение задачи о планировании договоров и оперативной компенсации сбоев в сырьевых поставках.
Оценочные средства для контроля освоения дисциплины «Основы математического моделирования социально-экономических процессов»
и учебно-методическое обеспечение самостоятельной работы студентов
Темы семинарских занятий:
1. Допустимые и оптимальные решения. Причины их возможного отсутствия. Определения максимума и минимума на допустимом множестве.
2. Итерационная схема построения оптимального решения через допустимые.
3. Задача максимизации прибыли при ограниченных сверху затратах эквивалентна задаче о минимизации затрат при ограниченной снизу прибыли на том же допустимом множестве).
4. Необходимые условия и достаточные условия для локальных экстремумов гладких функций. Матрица Гессе. Достаточное условие локального максимума в угловой точке. Условия Куна-Таккера, геометрическая интерпретация.
5. Многошаговые процедуры управления. Аналитическое решение задачи о
планировании договоров и оперативной компенсации сбоев в сырьевых поставках.
|
|
Типовые вопросы и задачи для контрольной работы
1. На множестве целых чисел N задано отображение «иметь общий остаток от деления на 7». На сколько классов эквивалентности разбивается множество N.
2. На множестве вещественных чисел R задано отображение «равенство», разбивающее множество R на классы эквивалентности. Сколько элементов содержится в каждом классе
3. Доказать равенства: a) А – В = АÇ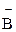 
, b) А D В = АÇ + 
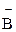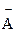ÇВ
c) (А È В)Ç С = (АÇС) È (ВÇС)
d)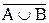 
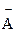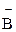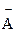= Ç , e) È =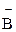 
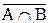
4. Изобразить на плоскости множество точек A x B, удовлетворяющих условиям
А = { x | xÎ R, -2 £ x £ 1}
B = { y | yÎ Z, -3 £ y £ 0}
5. Записать для высказывания формулу исчисления:
Р =” если F делится на 2 и не делится на 3, то оно не делится на 6 ”. Результатом будет: А = «F делится на 2», В = «F не делится на 3», и С = «F не делится на 6». Формула исчислений примет вид: P = (А Ù В) ® С.
Типовые вопросы и задачи для домашнего задания
Будет ли логическая формула тавтологией ((R1 ®ù R2) Ù R3) ® (R2 ® (ù R1 Ù R3))
2. Свести функцию к булевой функции от одной переменной
 | |
f(x,y,z) = x (y z Ú y z) Ú (x y z) (x y z)
3. П остроить СДНФ: f (x1, x2 , x3) = [ (х3 Û х1) ® х2 ]Ú (х3 Ùù х 1 )
4. Задача коммивояжера Найти минимальный по стоимости марщрут торговца
Вершины (1, 2), (2, 1), (1, 4), (4, 1), (3, 1), (2, 3), (3, 2), (3, 7), (7, 3), (4, 5), (5, 4)
Ребра 1 2 3 4 5 6 7 8 9 10 11
Стоимость 1 1 2 2 2 1 1 3 2 4 1
Вершины (5, 6), (6, 7), (7, 6), (6, 8), (8, 5), (8, 7)
Ребра 12 13 14 15 16 17
Стоимость 1 2 3 1 2 1
5. Привести к конъюнктивной нормальной форме (КНФ)
|
|
1) ù xy Ú ù x (y Ú x z) =? = (xy Ú ù x y Úù x x z) = x y Ú ù x y
2)y (x Úù y) Ú x (ù y Ú x ù z) =?
Типовые вопросы и задачи для экзамена
1. Записать операцию «дизъюнкция» для А и В через операции отрицание и конъюнкцию.
2. Задано множество А = {2, 3, 4, 6, 7} и отношения R =”быть делителем”, Q = “иметь один и
тот же остаток от деления на 3 ”. Записать отношение D = Q-1 – R и все его свойства.
3. Множество S ={1,2,3,4,5}, семейство Á: S1={2,3,4}, S2={2,5}, S3={3,4}, S4={1,5}, S5={2,3}.
Найти все трансверсали для Á
4. Заданы предпочтения Р(m1 )= w1 w3 w2 , Р(m2 )= w1 w2 w3 , Р(m3 )= w3 w1 w2
Р(w1)=m1m2m3, Р(w2)=m2 m3 m1 , Р(w3 )= m1m3 m2. Построить оптимальные паросочетания.
5. Заданы отношения R={(2,1), (3, 2), (4,3)}, Q={(1,3),(2,4),(3,3)}. Записать композицию R ° Q..
6. Отношение R транзитивно и антирефлективно. Показать, будет ли R-1 асимметрично.
7. Построить minСДНФ для функции f(x1,х2) = (ù х1 Ú (х 2®х 1)) Û х2
8. Найти диаметр, центр и радиус графа, заданного списком: «ребра ® вершины »
1 ® (1, 2), 2 ® (2, 3), 3 ® (2, 4), 4 ® (4, 5), 5 ® (5, 6), 6 ® (6, 7), 7 ® (6, 8)
9. Сколько классов эквивалентности содержит разбиение целых чисел по отношению
R= ” иметь общий остаток от деления на 4”
10. Привести СКНФ (x Ú y) (ù х Ú y)(x Ú ù y) к СДНФ.