Вопросы для подготовки к экзамену – 1 семестр
- Числовые функции. Способы задания и свойства.
- Обратные и сложные функции. Классификация элементарных функций.
- Предел числовой последовательности. Предел функции в бесконечности (
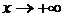 ).
). - Предел функции в точке. Односторонние пределы.
- Бесконечно малые функции и их свойства. Эквивалентные бесконечно малые.
- Бесконечно большие функции и их свойства.
- Теоремы о связи бесконечно малой функции и функции, имеющей предел, о единственности предела.
- Теорема об ограниченности функции, имеющей предел.
- Теоремы о пределе суммы, произведения и частного.
- Теоремы существования предела.
- Первый замечательный предел.
- Второй замечательный предел. Сложные проценты.
- Непрерывные функции. Условие непрерывности. Точки разрыва.
- Свойства функций, непрерывных на отрезке.
- Задачи, приводящие к понятию производной. Определение производной. Экономический смысл производной.
- Непрерывность и дифференцируемость функций.
- Основные правила дифференцирования.
- Производные элементарных функций. Таблица производных.
- Дифференциал функции. Инвариантность формы дифференциала. Применение дифференциала.
- Основные теоремы дифференциального исчисления (теоремы Ферма, Роля, Лагранжа, Коши).
- Правило Лопиталя.
- Монотонность функции в промежутке.
- Экстремумы функции. Необходимое и достаточное условия.
- Направление выпуклости графика функции, точки перегиба.
- Асимптоты графика функции. Схема исследования функции и построение графика.
- Функции многих переменных. Основные понятия.
- Частные производные первого и высших порядков.
- Частные и полные дифференциалы функции многих переменных.
- Производная по направлению, градиент функции в точке.
- Экстремумы функции многих переменных. Необходимые и достаточные условия.
- Условный экстремум функции многих переменных. Метод Лагранжа.
- Эмпирические формулы. Метод наименьших квадратов.
Вопросы для подготовки к экзамену за 2 семестр.
1. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла.
2. Таблица интегралов. Вычисление интегралов методом разложения.
3. Замена переменной и интегрирование по частям в неопределенном интеграле.
4. Интегрирование рациональных функций.
5. Интегрирование иррациональных функций.
6. Интегрирование тригонометрических функций.
7. Задачи, приводящие к определенному интегралу. Геометрический и экономический смысл определенного интеграла.
8. Свойства определенного интеграла.
9. Определенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
10. Методы вычисления определенного интеграла.
11. Несобственные интегралы.
12. Геометрические и экономические приложения определенного интеграла.
13. Дифференциальные уравнения. Общие понятия.
14. Дифференциальные уравнения первого порядка. Геометрическая интерпретация. Задача Коши.
15. Интегрируемые типы дифференциальных уравнений первого порядка.
16. Дифференциальные уравнения второго порядка, допускающие понижение порядка.
17. Линейные однородные уравнения второго порядка. Структура общего решения.
18. Линейные неоднородные уравнения второго порядка. Структура общего решения.
19. Линейные однородные ДУ второго порядка с постоянными коэффициентами.
20. Линейные неоднородные ДУ второго порядка с постоянными коэффициентами. Метод вариации произвольной постоянной.
21. Метод подбора частных решений для линейных ДУ второго порядка в случае:
а) 
б)  .
.
22. Понятие о системе линейных дифференциальных уравнений.
23. Числовые ряды. Общие понятия. Необходимый признак сходимости.
24. Знакоположительные ряды. Признаки сравнения.
25. Достаточные признаки сходимости для положительных рядов (Даламбера, Коши, Интегральный признак).
26. Знакопеременные ряды. Абсолютная и условная сходимость.
27. Знакочередующиеся ряды. Признак Лейбница.
28. Степенные ряды. Теорема Абеля.
29. Свойства суммы степенного ряда.
30. Разложение в ряд Тейлора, Маклорена.
31. Разложение в ряд элементарных функций ( ). Формулы Эйлера.
). Формулы Эйлера.
Учебно-методическое и информационное обеспечение дисциплины (модуля) « Математический анализ»:
Основная литература:
1. Высшая математика для экономистов: Учебник /Под ред. Н.Ш. Кремера. - 2-е изд., перераб. и доп. - М.: ЮНИТИ, 2004. - 573 с.
2. Практикум по высшей математике для экономистов: Учеб. пособие/ Под ред. Н.Ш.Кремера. - М.: ЮНИТИ, 2002. - 423 с.
3. Основы математического анализа: Учебник для вузов: В 2-х ч. Ч.2 / В. А. Ильин,, Э. Г. Позняк. - М.: Физматлит, 2002. - 464 с.
4. Сборник задач по высшей математике: Учеб. пособие для втузов / В. П. Минорский,. - 14-е изд. - М.: Издательство физико-математической литературы, 2004. - 336 с.
5. Солодовников А.С. Математика в экономике: Учебник: в 3-х ч. - М.: Финансы и статистика, 1998. - 224 с.
Дополнительная литература:
1. Математический анализ для экономистов: Учебник/ О.И. Ведина, В.Н. Десницкая, Г.Б. Варфоломеева, под ред. А.А. Гриба. – 2-е изд., перераб. и доп. – СПб.: Лань, 2004. – 344 с.
2. Математика для экономических специальностей: Учебник для вузов/ М.С. Красс, - 4-е изд., испр. – М.: Дело, 2003. – 704 с.
3. Математический анализ для экономистов: Учебник/ О.И. Ведина, В.Н. Десницкая, Г.Б. Варфоломеева, под ред. А.А. Гриба. – 2-е изд., перераб. и доп. – СПб.: Лань, 2004. – 344 с.
4. Сборник задач и упражнений по математическому анализу: учебное пособие для вузов/ Б.П. Демидович. – М.: АСТ, 2006. – 558 с.
Линейная алгебра
Вопросы для подготовки к экзамену
1. Определители и их свойства.
2. Минор. Алгебраическое дополнение. Разложение определителя по элементам строки (столбца).
3. Матрицы. Основные определения.
4. Линейные операции над матрицами.
5. Обратная матрица.
6. Системы линейных алгебраических уравнений. Метод Крамера решения СЛАУ.
7. Системы линейных алгебраических уравнений. Матричный способ решения СЛАУ.
8. Системы линейных алгебраических уравнений. Метод Гаусса решения СЛАУ.
9. Векторы. Основные определения. Арифметические операции над векторами.
10. Декартовы координаты вектора в пространстве. Операции над векторами, заданными в координатной форме.
11. Скалярное произведение векторов. Свойства скалярного произведения.
12. Скалярное произведение векторов, заданных в координатной форме.
13. Тройки векторов. Векторное произведение векторов. Свойства векторного произведения.
14. Векторное произведение векторов, заданных в координатной форме.
15. Смешанное произведение трех векторов.
16. Смешанное произведение векторов, заданных в координатной форме.
17. Линейная зависимость векторов.
18. Базис и размерность векторного пространства.
19. Плоскость в пространстве.
20. Взаимное расположение плоскостей.
21. Прямая в пространстве.
22. Взаимное расположение прямых в пространстве.
23. Прямая на плоскости.
24. Кривые второго порядка. Эллипс.
25. Кривые второго порядка. Гипербола.
26. Кривые второго порядка. Парабола.
27. Квадратичные формы.
28. Комплексные числа.
Учебно-методическое и информационное обеспечение дисциплины (модуля): «Линейная алгебра»
Основная литература:
1. Высшая математика для экономистов: Учебник /Под ред. Н.Ш. Кремера. - 2-е изд., перераб. и доп. - М.: ЮНИТИ, 1999. - 471 с.
2. Солодовников А.С. Математика в экономике: Учебник: в 3-х ч. - М.: Финансы и статистика, 1998. - 224 с.
3. Практикум по высшей математике для экономистов: Учеб. пособие / Под ред. Н.Ш. Кремера. - М.: ЮНИТИ, 2002. - 423 с.
4. Математика для экономических специальностей: Учебник для вузов/ М.С. Красс, - 4-е изд., испр. – М.: Дело, 2003. – 704 с.
Дополнительная литература:
1. Гусак А.А. Аналитическая геометрия и линейная алгебра: Справочное пособие к решению задач / А. А. Гусак,. - 2-е изд., стереотип. - Мн.: ТетраСистемс, 2001. - 288 с..
2. Линейная алгебра: Учебник для вузов / В. А. Ильин,; В.А.Ильин, Э.Г. Позняк. - 5-е изд., стереотип. - М.: Физматлит, 2001. - 320 с.
Методические разработки:
1. Миловидов И.Д. Задачи по линейной алгебре и аналитической геометрии для экономических специальностей. Йошкар-Ола: МарГУ, 2007. – 120 с.