РОСЖЕЛДОР
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Ростовский государственный университет путей сообщения»
(ФГБОУ ВПО РГУПС)
Факультет – Энергетический
Кафедра «Информатика»
Специальность 190401 – «Электроснабжение железных дорог»
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
на тему:
«СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СИСТЕМ ЭЛЕКТРОСНАБЖЕНИЯ»
Студент группы
ЭС-III-173 ________________ Литвинцов А.И.
Работа защищена ________________
Дата ________________
Руководитель работы ________________ Линденбаум Т.М.
ЗАДАНИЕ
на расчетно-графическую работу
по дисциплине «Математическое моделирование систем и процессов»
1. Произвести моделирование случайной величины в EXCEL по заданному варианту методом Монте-Карло.
1.1. С помощью функции СЛЧИСзаполнить таблицу требуемым количеством случайных величин, равномерно распределённых в интервале (0;1).
1.2. В соответствии с заданным законом распределения рассчитать значения исследуемого показателя.
1.3. Скопировать значения исследуемого образца как числа.
1.4. Упорядочить полученную статистику по возрастанию.
2. Произвести обработку статистических данных.
2.1. Оценивание методом моментов.
2.1.1. Рассчитать числовые характеристики: математическое ожидание, дисперсию, среднее квадратическое отклонение (стандартное отклонение), коэффициент вариации.
2.1.2. Рассчитать границы доверительного интервала для математического ожидания.
2.1.3. Рассчитать параметры закона распределения и сравнить их с заданными значениями, оценить относительную погрешность.
2.2. Сглаживание статистических данных.
|
|
2.2.1. Рассчитать и построить на одном графике эмпирическую и теоретическую функции распределения.
2.2.2. Сгруппировать статистические данные.
2.2.3. Рассчитать эмпирическую плотность распределения (гистограмму), теоретическую плотность распределения и построить их на одном графике.
2.3. Проверка статистической гипотезы о законе распределения.
2.3.1. Проверить по критерию Колмогорова гипотезу о том, что закон распределения не противоречит статистическим данным.
3. Проанализировать полученные результаты и сделать выводы.
| № варианта | Исследуемый показатель | Закон распределения | Параметры за-кона распре-деления | Число реализаций |
| Ток фидера тяговой подстанции переменного тока (А) | Нормальный |  =1460 А =1460 А
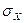 =120А =120А
|
Содержание
Введение…………………………………………………………………………..5
1. Моделирование случайной величины интервала между попутно следующими поездами методом Монте – Карло……………………………….7
2. Обработка статистических данных……………………………………….9
2.1. Оценивание…………………………………………………………………9
2.2. Сглаживание………………………………………………………………13
2.2.1. Построение статистической и теоретической функции распределения…………………………………………………………………....13
2.2.2. Построение статистической и теоретической плотности распределения……………………………………………………………………15
2.3. Проверка статистических гипотез о законе распределения……………18
2.3.1. Проверка статистической гипотезы закона распределения по критерию Колмогорова……………………………………………………………………...18
|
|
2.3.2. Проверка статистической гипотезы закона распределения по критерию Пирсона…………………………………………………………………………..19
Заключение………………………………………………………………………22
Список использованных источников…………………………………………..23
Введение
Высказывания великих ученых, без дополнительных комментариев, дают полное представление о роли и значении математики, как в научно-теоретической, так и предметно-практической деятельности специалистов.
Математическое моделирование - это теоретико-экспериментальный метод познавательно-созидательной деятельности, это метод исследования и объяснения явлений, процессов и систем на основе создания новых объектов- математических моделей.
Под математической моделью принято понимать совокупность соотношений (уравнений, неравенств, логических условий, операторов и т.п.), определяющих характеристики состояний объекта моделирования, а через них и выходные значения.
Таким образом, на "модельном" этапе математизации, т.е. этапе математического моделирования, осуществляется попытка теоретического воспроизведения, "теоретической реконструкции" объекта-оригинала в форме другого объекта - математической модели.
Математическое моделирование рассматривает модели, полученные на основе данных математической статистики. Разрабатываются методы анализа статистических данных в зависимости от целей исследования, рассматриваются различные способы сбора и группировки статистических сведений. Для более удобного анализа математической статистики применяют два вида моделей:
|
|
Ø аналитические;
Ø статистические.
Первые более приспособлены для поиска оптимальных решений, отчетливо отражают присущие явлению основные закономерности, но при этом более грубы, учитывают меньшее число факторов, всегда требуют каких – то допущений и упрощений.
Вторые более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое число факторов, но при этом более громоздкие, плохо обозримые. Но при этих недостатках статистические модели применяют для анализа любой системы, хотя времени тратится намного больше.
В наше время при использовании сложных систем применяются модели, сочетающие в себе оба вида. Но правильное описание аналитических и статистических методов в исследовании операций – дело искусства, чутья, и возможно только при большом опыте исследователя.
В данной расчетно-графической работе по характеру процессов во времени рассматриваются статистические модели, которые создаются на основе данных математической статистики.
Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования.
1. Моделирование случайной величины интервала между попутно следующими поездами методом Монте-Карло
В данной работе необходимо смоделировать выборку случайных величин. Для этого используем программу Excel. С помощью функции СЛЧИС заполняем таблицу из 210 случайных чисел.
Датчик случайных чисел позволяет сгенерировать выборку значений равномерно распределенной случайной величины. Нам необходимо получить выборку значений случайной величины, распределенной по нормальному закону распределения.
Для перехода от равномерно распределенной случайной величины r, получаемой с помощью датчика случайных чисел, к необходимой нам величине х, распределенной по нормальному закону, воспользуемся методом основанном на математическом смысле случайной величины.
Функция распределения F(x) для нормальногозакона распределения:
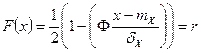
Сгенерируем выборку с помощью датчика случайной величины и преобразуем равномерно распределенную величину r в искомую х. Результаты представлены в таблице 1.1.
Формула переменной x для нормального закона: 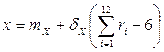 .
.
| № | r1 | r2 | … | r11 | r12 | сумма | x | Xф |
| 0,727148 | 0,551398 | … | 0,921293 | 0,517513 | 6,338641 | 1500,637 | 1319,826 | |
| 0,460269 | 0,795547 | … | 0,53709 | 0,057495 | 6,070177 | 1468,421 | 1405,734 | |
| 0,227209 | 0,904868 | … | 0,238315 | 0,487889 | 6,6743 | 1540,916 | 1699,582 | |
| 0,653912 | 0,886977 | … | 0,21207 | 0,550707 | 5,655574 | 1418,669 | 1429,684 | |
| 0,052648 | 0,514364 | … | 0,6679 | 0,141252 | 4,075007 | 1229,001 | 1201,07 | |
| 0,991712 | 0,098999 | … | 0,634509 | 0,629567 | 6,470723 | 1516,487 | 1467,928 | |
| 0,400736 | 0,573488 | … | 0,030119 | 0,985649 | 6,54689 | 1525,627 | 1407,946 | |
| 0,345891 | 0,214636 | … | 0,635857 | 0,653344 | 6,284106 | 1494,093 | 1255,579 | |
| 0,749063 | 0,068166 | … | 0,260558 | 0,440535 | 5,556509 | 1406,781 | 1579,458 | |
| 0,210818 | 0,980364 | 0,195935 | 0,585197 | 4,522998 | 1282,76 | 1523,343 | ||
| …. | …. | …. | … | …. | …. | …. | …. | …. |
| 0,960495 | 0,125153 | … | 0,614844 | 0,844306 | 6,228103 | 1487,372 | 1560,52 | |
| 0,454735 | 0,664281 | … | 0,91238 | 0,621495 | 7,580986 | 1649,718 | 1555,165 | |
| 0,962639 | 0,920836 | … | 0,853648 | 0,181416 | 6,781819 | 1553,818 | 1274,261 | |
| 0,139158 | 0,832817 | … | 0,675959 | 0,448046 | 5,455447 | 1394,654 | 1555,931 | |
| 0,295979 | 0,703607 | … | 0,424692 | 0,558844 | 7,404096 | 1628,492 | 1455,226 | |
| 0,392491 | 0,8587 | … | 0,152439 | 0,52234 | 6,844597 | 1561,352 | 1476,598 | |
| 0,824701 | 0,962792 | … | 0,8144 | 0,45448 | 7,071734 | 1588,608 | 1458,838 | |
| 0,160515 | 0,506448 | … | 0,824588 | 0,482613 | 5,557615 | 1406,914 | 1698,347 | |
| 0,356116 | 0,209172 | … | 0,393565 | 0,343892 | 4,477888 | 1277,347 | 1415,637 | |
| 0,18013 | 0,072021 | … | 0,465622 | 0,647158 | 5,227187 | 1367,262 | 1288,931 | |
| 0,89096 | 0,064543 | … | 0,248851 | 0,159142 | 5,449016 | 1393,882 | 1516,942 |
Таблица 1.1 – выборка и её обработка
В результате была смоделирована выборка случайной величины тока фидера тяговой подстанции переменного тока, распределенной по нормальному закону распределения.
2. Обработка статистических данных
Обработка статистических данных включает в себя:
ü Оценивание.
ü Сглаживание.
ü Проверка статистической гипотезы.
2.1. Оценивание.
Оценивание – это определение вероятности случайных событий, числовых характеристик и параметров закона распределения.
Для оценки статистических данных необходимо определить следующие характеристики случайной величины тока фидера тяговой подстанции переменного тока: математическое ожидание, дисперсию, среднеквадратическое отклонение, коэффициент вариации, третий центральный момент, асимметрию, четвёртый центральный момент и эксцесс. Также необходимо определить доверительный интервал для математического ожидания 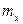 .
.
Оптимальные статистические оценки, перечисленных числовых характеристик определяем методом моментов.
Математическое ожидание: 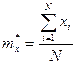 ,
,
где xi – значение случайной i -ой величины в опыте.
N – число опытов.
Дисперсия: 
Среднеквадратическое отклонение: 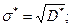
Коэффициент вариации: 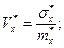
Третий центральный момент: 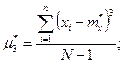
Асимметрия: 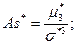
Четвёртый центральный момент: 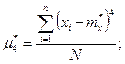
Эксцесс: 
Чтобы узнать насколько реальное математическое ожидание отличается от оцениваемого, воспользуемся доверительным интервалом.
Доверительный интервал – это интервал, который с заданной доверенной вероятностью g накрывает неизвестные значения параметра. g=0,95
Границы доверительного интервала определим по формулам:
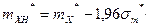
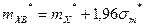
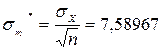
Числовые характеристики:
· Математическое ожидание:  А
А
· Дисперсия: 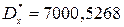
· Среднее квадратическое отклонение: 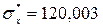 А
А
· Третий центральный момент: 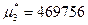
· Четвертый центральный момент: 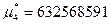
· Коэффициент вариаций: 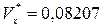
· Асимметрия: 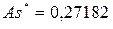
· Эксцесс: 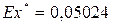
· Границы доверительного интервала: 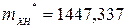 А
А
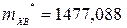 А
А
Как видно из расчетов 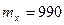 А действительно лежит внутри доверительного интервала
А действительно лежит внутри доверительного интервала  .
.
Расчет числовых характеристик из Excel приведен в таблице 2.1
| № | X в.р | x-mx | (x-mx)2 | (x-mx)3 | (x-mx)4 |
| 1186,229 | -275,984 | 76167,07 | -21020879 | ||
| 1196,445 | -265,768 | 70632,5 | -18771843 | ||
| 1201,07 | -261,142 | 68195,28 | -17808671 | ||
| 1208,578 | -253,635 | 64330,52 | -16316446 | ||
| 1210,216 | -251,997 | 63502,3 | -16002366 | ||
| 1243,176 | -219,036 | 47976,75 | -10508632 | ||
| 1255,579 | -206,633 | 42697,27 | -8822674 | ||
| 1260,517 | -201,696 | 40681,2 | -8205229 | ||
| 1266,046 | -196,166 | 38481,25 | -7548729 | ||
| 1269,311 | -192,901 | 37210,96 | -7178049 | ||
| ………. | ………….. | ……….. | ……….. | ………… | ……….. |
| 1673,978 | 211,7659 | 44844,8 | |||
| 1677,264 | 215,0518 | 46247,29 | |||
| 1677,275 | 215,0629 | 46252,06 | |||
| 1692,51 | 230,298 | 53037,16 | |||
| 1694,405 | 232,1923 | 53913,27 | |||
| 1698,347 | 236,1342 | 55759,36 | |||
| 1699,582 | 237,3693 | 56344,18 | |||
| 1723,041 | 260,8286 | 68031,57 | |||
| 1760,243 | 298,0311 | 88822,51 | |||
| 1828,404 | 366,1918 | 134096,5 | 1,7982E+10 | ||
| 1887,725 | 425,5123 | 181060,8 | 3,2783E+10 | ||
| сумма | 365553,1 | 1,17E+08 | 1,5814E+11 | ||
| M*x= | 1462,212 | V*x= | 0,08207 | ||
| D*x= | 14400,79 | 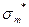 = =
| 5,77372 | ||
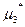 = =
| 30775,6262 | m*нx= | 1447,337 | ||
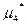 = =
| m*вx= | 1477,088 | |||
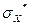
| 120,003 | ||||
| As*= | 0,271827 | ||||
| Ex*= | 0,05024513 |
Таблица 2.1
В результате оценивания статистических данных были получены оптимальные оценки числовых характеристик, а также верхняя и нижняя границы доверительного интервала для реального 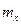 тока фидера тяговой подстанции переменного тока.
тока фидера тяговой подстанции переменного тока.
2.2. Сглаживание.
Сглаживание – это составление математической модели процесса, соответствующей статистическим данным, в частном случае определение закона дискретной или непрерывной случайной величины и т. д.
Возможны два случая: когда физическая природа явления или исследование аналогов позволяет сделать предположение о законе распределения и когда вид закона распределения выбирается на основе анализа этих же статистических данных. В последнем случае выбор закона осуществляют путём сравнения статистической функции распределения или статистической плотности распределения с известными теоретическими законами распределения. В некоторых случаях можно выбирать закон распределения путём сравнения статистических и теоретических числовых характеристик.
Для выбора математической модели описывающей ток фидера тяговой подстанции переменного тока необходимо построить статистические функцию и плотность распределения и сравнить их с теоретическими.