Интеграл Фурье для четной и нечетной функции
Пусть f (x)-четная функция, удовлетворяющая условиям представимости интегралом Фурье.
Учитывая, что 
, а также свойство интегралов по симметричному относительно точки x =0 интервалу от четных функций, из равенства (2) получаем:
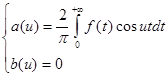(3)
Таким образом, интеграл Фурье четной функции f (x) запишется так:
,
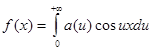где a (u) определяется равенством (3).
Рассуждая аналогично, получим, для нечетной функции f (x):
(4)
и, следовательно, интеграл Фурье нечетной функции имеет вид:
,
где b (u) определяется равенством (4).
Комплексная форма интеграла Фурье
, (5)
где
.
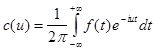Выражение в форме (5) является комплексной формой интеграла Фурье для функции f (x).
Если в формуле (5) заменить c (u) его выражением, то получим:
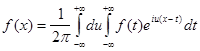, где правая часть формулы называется двойным интегралом
Фуpье в комплексной форме. Переход от интеграла Фурье в комплексной форме к интегралу
в действительной форме и обратно осуществим с помощью формул:
Формулы дискретного преобразования Фурье
Обратное преобразование Фурье.
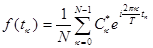
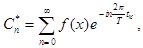
где n =1,2,..., k =1,2,...
Дискретным преобразованием Фурье - называется N -мерный вектор 
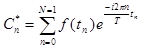
при этом,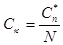 
.
Разложение четной функции в ряд
Данную выше функцию сделаем четной(см. теорию), и рассмотрим ее на промежутке от 0 до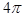 
смотри рис.2
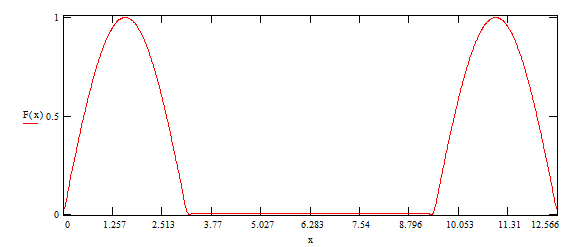
Рис.2
поэтому разложение по косинусу имеет вид:
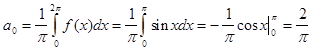
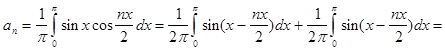
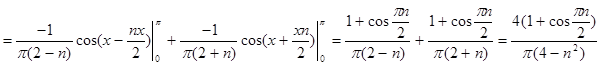
Из разложения видим что при n =2 дробь теряет смысл поэтому отдельно рассмотрим разложения первого и второго коэффициента суммы:
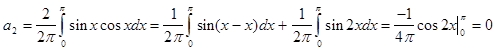
На основе данного разложения запишем функцию в виде ряда:
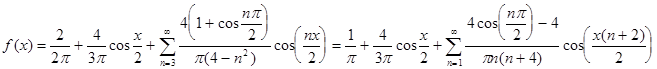
и вообще
.
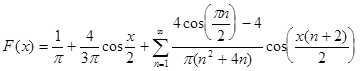Найдем первые пять гармоник для найденного ряда:
1-ая гармоника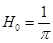 
2-ая гармоника 
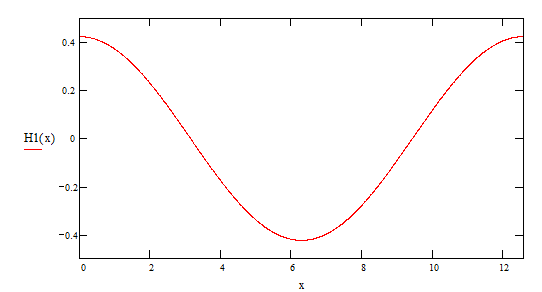
3-я гармоника 
4-ая гармоника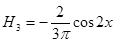 
5-ая гармоника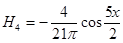 
А теперь рассмотрим сумму этих гармоник F(x):
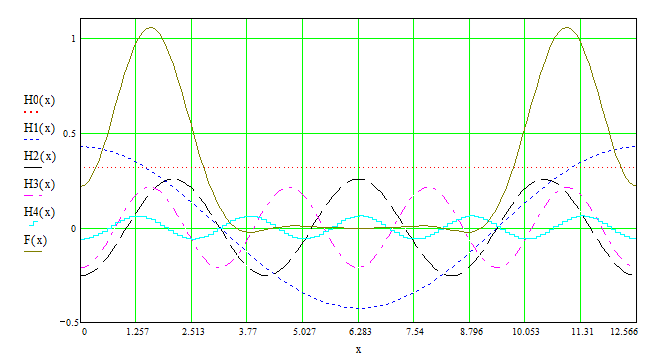
Комплексная форма ряда по косинусам
Для рассматриваемого ряда получаем коэффициенты (см. гл.1)
,
но при 
не существует, поэтому рассмотрим случай когда n =+2:
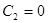(т.к.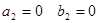 
см. разложение выше)
и случай когда n =-2:
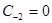(т.к.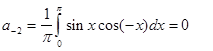 
)
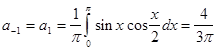
И вообще комплексная форма:
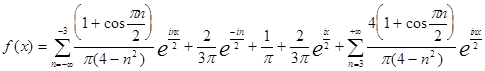
или
или
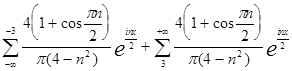
Разложение нечетной функции в ряд
Аналогичным образом поступаем с данной функцией F(x), продлевая ее как нечетную, и рассматриваем на промежутке от 0 до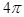 
смотри рис.3
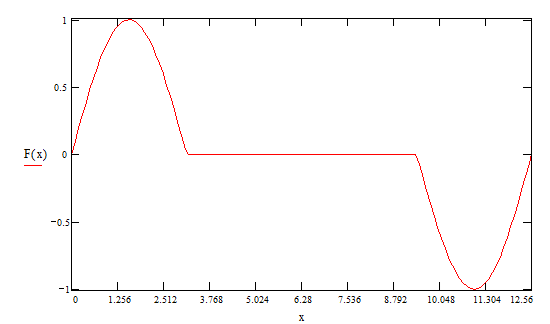
Рис.3
поэтому разложение по синусам имеет вид:
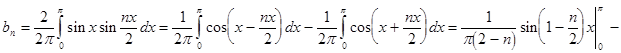
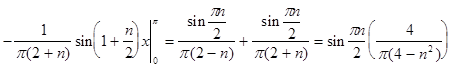
Из данного разложения видно, что при n =2 произведение неопределенно (можно не учесть часть суммы), поэтому рассмотрим два отдельных случая.
При n =1:
,
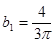и при n =2:
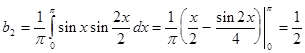
Учитывая данные коэффициенты имеем разложения в виде
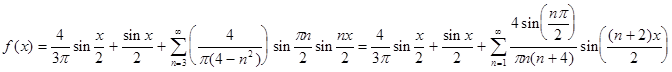
и вообще
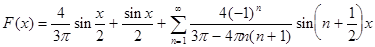
Найдем первые пять гармоник для данного разложения:
1-ая гармоника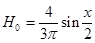 
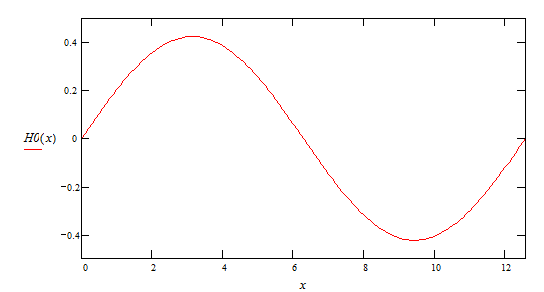
2-ая гармоника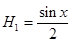 
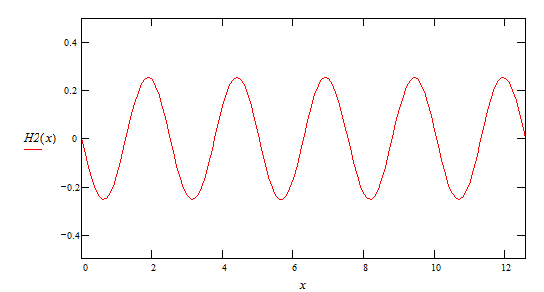
3-ая гармоника 
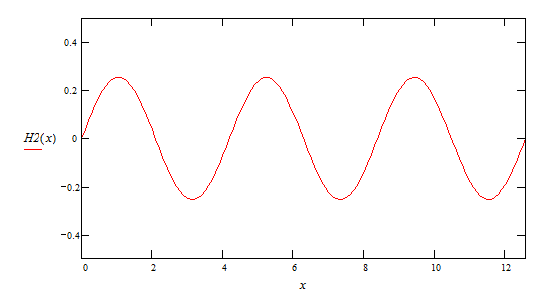
4-ая гармоника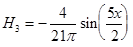 
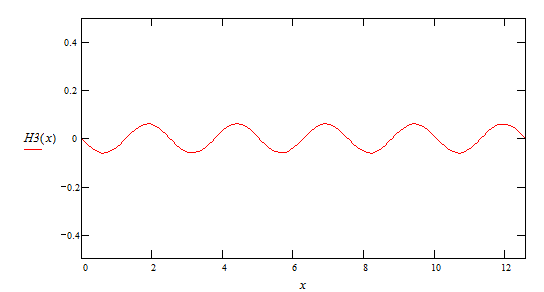
5-ая гармоника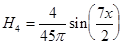 
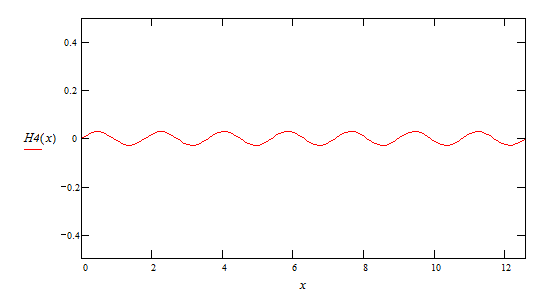
И просуммировав выше перечисленные гармоники получим график функции F (x)
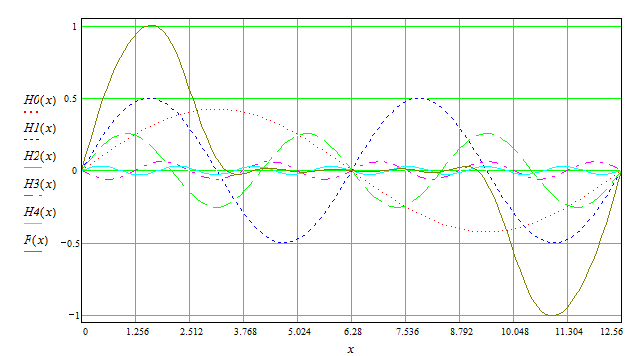Вывод:
На основании главы 2, разложение функции в тригонометрический ряд(рис.1), разложение в ряд по косинусам(рис.2), разложение по синусам(рис.3), можно заключить, что данная функция разложима в тригонометрический ряд и это разложение единственное. И проанализировав суммы первых пяти гармоник по каждому разложению можно сказать, что наиболее быстрее к заданному графику достигается при разложении по синусам.
Комплексная форма ряда по синусам
Основываясь на теорию (см. гл.1) для ряда получаем:
, 
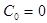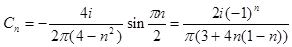(т.к.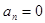 
)
тогда комплексный ряд имеет вид:
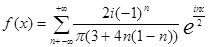
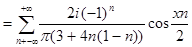
ГЛАВА 3 ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
Проверка условий представимости
Данную ранее функцию (см. гл. 2) доопределим на всей прямой от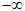 
до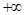 
как равную нулю(рис.4).
Рис.4
а) f(x)-определенна на R;
б) f(x) возрастает на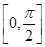 
, f(x) убывает на 
- кусочнo-монотонна.
f(x) = const на 
и 
.
< 
.
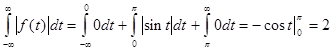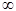Интеграл Фурье
В соответствии с теорией (см. гл. 1) найдем a (u) и b (u):
;
.
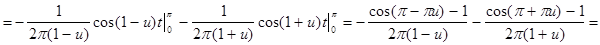
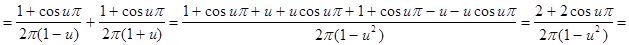
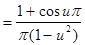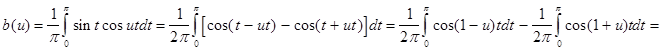
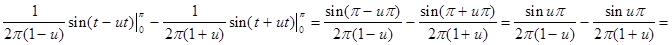
И в конечном варианте интеграл Фурье будет выглядеть так:
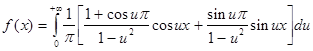
Интеграл Фурье в комплексной форме
Теперь представим интеграл Фурье в комплексной форме. На основе выше полученных разложений имеем:
,
,
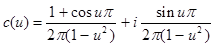а теперь получим интеграл в комплексной форме:
.
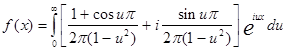