Основные сведения
Функцию можно разложить в ортонормированной системе пространства X=[-1,1], причем полиномы получим, если проинтегрируем выражение:
Соответственно получим для n=0,1,2,3,4,5,...:
..........
Для представления функции полиномом Лежандра необходимо разложить ее в ряд:
,
где 
и разлагаемая функция должна быть представлена на отрезке от -1 до 1.
Преобразование функции
Наша первоначальная функция имеет вид (см. рис. 1):
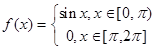
т. к. она расположена на промежутке от 0 до 
необходимо произвести замену, которая поместит функцию на промежуток от -1 до 1.
Замена:
и тогда F(t) примет вид
или
Вычисление коэффициентов ряда
Исходя из выше изложенной формулы для коэффициентов находим:
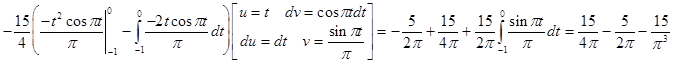
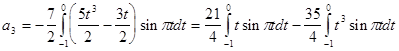
Далее вычисление коэффициентов осложнено, поэтому произведем вычисление на компьютере в системе MathCad и за одно проверим уже найденные:
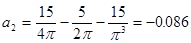
Рассмотрим процесс стремления суммы полинома прибавляя поочередно 
- слагаемое:
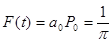
А теперь рассмотрим график суммы пяти полиномов F (t) на промежутки от -1 до 0 (рис.5):
Рис. 5
т.к. очевидно, что на промежутке от 0 до 1 будет нуль.
Вывод:
На основе расчетов гл.2 и гл.4 можно заключить, что наиболее быстрое стремление из данных разложений к заданной функции достигается при разложении функции в ряд.
ГЛАВА 5 ДИСКРЕТНЫЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ
Прямое преобразование
Для того, чтобы произвести прямое преобразование, необходимо задать данную функцию (гл. 1, рис. 1) таблично. Поэтому разбиваем отрезок от 0 до на N =8 частей, так чтобы приращение:
В нашем случае 
, и значения функции в k -ых точках будет:
для нашего случая 
(т.к. a =0).
Составим табличную функцию:
| k | ||||||||
| 0.785 | 1.571 | 2.356 | 3.142 | 3.927 | 4.712 | 5.498 | |
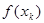
| 0.707 | 0.707 |
Табл. 1
Прямым дискретным преобразованием Фурье вектора 
называется 
. Поэтому найдем:
, n =0,1,..., N -1
Сумму находим только до 3 слагаемого, т.к. очевидно, что от 4 до 7 к сумме суммируется 0 (т.к. значения функции из таблицы равны нулю).
Составим таблицу по прямому дискретному преобразованию:
зная, 
, где 
, где 
| n | ||||||||
| ||||||||
| 2,4 | 0.4 | ||||||
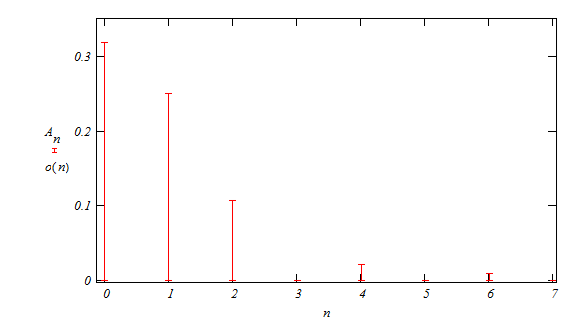
| 0.318 | 0.25 | 0.106 | 0.021 | 0.009 |
Табл. 2
Амплитудный спектр
Обратное преобразование
Обратимся к теории гл.1. Обратное преобразование- есть функция:
В нашем случаи это:
А теперь найдем модули 
и составим таблицу по обратным дискретным преобразованиям:
| k | ||||||||
| 0.785 | 1.571 | 2.356 | 3.142 | 3.927 | 4.712 | 5.498 | |
|
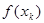
| 0.707 | 0.707 | ||||||
| 0.708 | 0.707 | 8e-4 | 5e-5 | 5e-4 | 3e-4 |
Табл. 3
Из приведенной таблицы видно, что 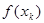приближенно равно 
.
Построим графики используя табл.3, где 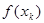- это F (k), а 
- это f (k) рис. 6:
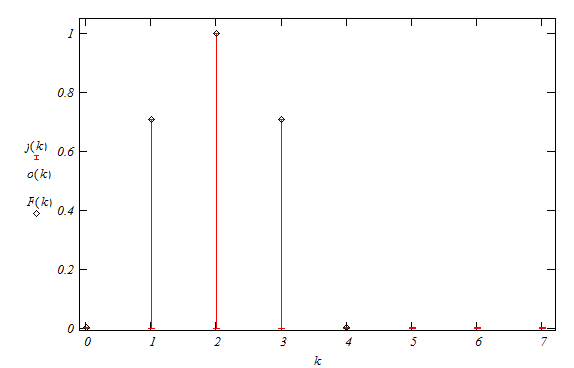
Рис. 6
Вывод:
На основе проделанных расчетов можно заключить, что заданная функция представима в виде тригонометрического ряда Фурье, а также интеграла Фурье, полинома Лежандра и дискретных преобразований Фурье. О последнем можно сказать, что спектр (рис. 6) прямого и обратного преобразований совпадают с рассматриваемой функцией и расчеты проведены правильно.
Этап I
Постановка задачи
Дана основная (рис. 1.1а) и резервная (рис. 1.1б) схемы. Рассмотреть два способа повышение надежности основной схемы до уровня 0.95
а) б)
Рис. 1.1
Первый способ
- каждому элементу основной схемы подключаются параллельно по N резервных элементов имеющих надежность в два раза меньше, чем надежность элемента к которому подключают.
Второй способ
- подключить к основной схеме параллельно по N резервной схеме.
| № элемента | |||||||||
Надежность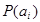 
| 0.6 | 0.6 | 0.6 | 0.3 | 0.7 | 0.4 | 0.3 | 0.5 | 0.1 |
Надеж.(резер.) 
| 0.3 | 0.3 | 0.3 | 0.15 | 0.35 |
Теоретическая часть
Ввиду важности операций сложения и умножения над событиями дадим их определение:
Суммой двух событий А и В называется событие С, состоящее в выполнении события А или события В, или обоих событий вместе.
Суммой нескольких событий называется событие, состоящее в выполнении хотя бы одного из этих событий.
Произведением двух событий А и В называется событие D, состоящее в совместном выполнении события А и события В.
Произведением нескольких событий называется событие, состоящее в совместном выполнении всех этих событий.
А к с и о м ы т е о р и и в е р о я т н о с т е й:
1. Вероятность любого события находится в пределах:
.
2. Если А и В несовместные события 
, то
3. Если имеется счетное множество несовместных событий А1, А2,... Аn,... 
при 
, то
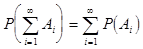
Следствие: сумма вероятностей полной группы несовместных событий равна единице, т.е. если
; 
при 
то
.
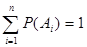Сумма вероятностей противоположных событий ровна единице:
Правило умножения вероятностей: вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого
.
Для независимых событий правило умножения принимает вид:
, или
Основываясь на теорию выведем некоторые формулы для решения поставленной задачи.
Схема состоит из нескольких n блоков (рис. 2.1), каждый из которых (независимо от других) может выйти из строя. Надежность каждого блока равна p. Безотказная работа всех без исключения блоков необходима для безотказной работы в целом. Найти вероятность безотказной работы всей схемы.
Рис. 2.1
Событие A ={безотказная работа прибора} есть произведение n независимых событий А 1, А 2,... Аn, где Ai ={безотказная работа i -го блока}. По правилу умножения для независимых событий имеем
.
Схема состоит из 2 блоков (рис. 2.2), каждый из которых (независимо от друг от друга) может выйти из строя. Надежность каждого блока равна p. Найти вероятность безотказной работы всей системы.
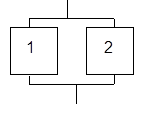
Рис. 2.2
От события В ={система будет работать} перейдем к противоположному: 
={система не будет работать}. Для того чтобы система не работала, нужно, чтобы отказали оба блока. Событие есть произведение двух событий:
={блок 1 отказал}x{блок 2 отказал}.
По правилу умножения для независимых событий:
Практическая часть
Воспользовавшись выше изложенными формулами рассчитаем надежность основной схемы (рис. 1а), она составит:
, а также резервной схемы (рис. 1б):
Рассмотрим первый способ подключения (смотри рис. 3.1), когда подключаем по N элементов до тех пор, пока 
Рис. 3.1
Тогда формула вероятности для схемы на рис. 2 будет выглядеть так:
, где
,
,
,
,
.
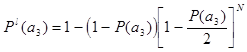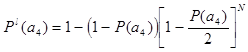Увеличивая N дополнительных элементов пошагово добиваемся значения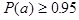 
:
Шаг первый, при N =1
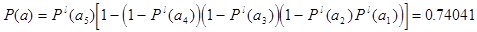< 0.95
Шаг второй, при N =2
< 0.95
Шаг третий, при N =3
< 0.95
Шаг четвертый, при N =4
< 0.95
Шаг пятый, при N =5
> 0.95
Из рассмотренных вычислений можно заключить, что для достижения заданной вероятности 0.95 необходимо пяти добавочных элементов.
Рассмотрим второй способ подключения к основной резервной схемы (рис. 3) и найдем число N подключений при котором достигается заданная вероятность 
.
Рис. 3.2
Формула по которой будет вычисляться вероятность схемы на рис. 3 выглядит так:
, где
, а 
- смотри выше.
Увеличивая N дополнительных резервных схем пошагово добиваемся значения 
:
При N =1: 
< 0.95
При N =2: 
< 0.95
При N =3: 
< 0.95
При N =4: 
< 0.95
При N =5: 
< 0.95
При N =6: 
> 0.95
Из рассмотренных вычислений можно заключить, что для достижения заданной вероятности 0.95 необходимо шесть резервных схем.
Этап II
Постановка задачи
- найти неизвестную константу функции f (x);
- выписать функцию распределения, построить их графики;
- найти математическое ожидание и дисперсию;
- найти вероятность попадания в интервал (1;4).
Теоретическая часть
Под случайной величиной понимается величина, которая в результате измерения (опыта) со случайным исходом принимает то или иное значение.
Функция распределения случайной величины Х называется вероятность того, что она примет значение меньшее, чем заданное х:
.
Основные свойства функции распределения:
1) F (x) - неубывающая функция своего аргумента, при 
.
2) 
.
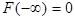3) 
.
Плотностью распределения непрерывной случайной величины Х в точке х называется производная ее функции распределения в этой точке. Обозначим ее f (x):
Выразим функцию распределения F (x) через плотность распределения f (x):
Основные свойства плотности распределения f (x):
1. Плотность распределения - неотрицательная функция 
.
2. Интеграл в бесконечных пределах от плотности распределения равен единицы:
.
Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений.
Перейдем от дискретной случайной величины Х к непрерывной с плотностью f (x).
Дисперсия случайной величины есть математическое ожидание квадрата соответствующей центрированной величины:
Для непосредственного вычисления дисперсии непрерывной случайной величины служит формула:
Практическая часть
Для нахождения неизвестной константы c применим выше описанное свойство:
, откуда 
, или
Найдем функцию распределения основываясь на теоретической части:
- на интервале 
- на интервале 
- на интервале 
Теперь построим график функций f (x)- плотности распределения (рис. 2.1 - кривая распределения) и F (x)- функции распределения (рис. 2.2)
Рис. 2.1
Рис. 2.2
Следуя постановке задачи найдем математическое ожидание 
и дисперсию 
для случайной величины X:
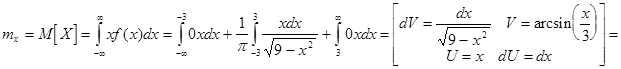
Производя еще одну замену 
приходим к первоначальной формуле из чего можно сделать вывод, что математическое ожидание с.в. Х равно:
Также находим дисперсию:
И последнее, вероятность попадания в интервал (1;4) находим как:
Этап III
Постановка задачи
Дана случайная выборка объема n =100:
| 104.6 | 95.2 | 82.0 | 107.7 | 116.8 | 80.0 | 100.8 | 124.6 | 99.4 | 101.4 |
| 100.6 | 86.3 | 88.2 | 103.8 | 98.5 | 111.8 | 83.4 | 94.7 | 113.6 | 74.7 |
| 114.3 | 86.9 | 106.6 | 94.9 | 105.9 | 88.6 | 96.6 | 93.7 | 90.8 | 96.5 |
| 110.2 | 100.0 | 95.6 | 102.9 | 91.1 | 103.6 | 94.8 | 112.8 | 100.1 | 95.3 |
| 113.9 | 113.9 | 86.1 | 110.3 | 88.4 | 97.7 | 70.1 | 100.5 | 90.9 | 94.5 |
| 109.1 | 82.2 | 101.9 | 86.7 | 97.4 | 102.1 | 87.2 | 94.71 | 112.4 | 94.9 |
| 111.8 | 99.0 | 101.6 | 97.2 | 96.5 | 102.7 | 98.6 | 100.0 | 86.2 | 89.4 |
| 85.0 | 86.6 | 122.7 | 101.8 | 118.3 | 106.1 | 91.3 | 98.4 | 90.4 | 95.1 |
| 93.1 | 110.4 | 100.4 | 86.5 | 105.4 | 96.9 | 101.9 | 83.8 | 107.3 | 107.5 |
| 113.7 | 102.8 | 88.7 | 112.5 | 79.4 | 79.1 | 98.1 | 103.8 | 107.2 | 102.3 |
Теоретическая часть
Под случайной выборкой объема n понимают совокупность случайных величин 
, не зависимых между собой. Случайная выборка есть математическая модель проводимых в одинаковых условиях независимых измерений.
Упорядоченной статистической совокупностью будем называть случайную выборку величины в которой расположены в порядке возрастания 
.
Размах выборки есть величина r=Xn-X1, где Xn - max, X1 - min элементы выборки.
Группированным статистическим рядом называется интервалы с соответствующими им частотами на которые разбивается упорядоченная выборка, причем ширина интервала находится как:
тогда частота попадания в отрезок 
находим по формуле:
, где Vi - число величин попавших в отрезок 
, причем 
. Поделив каждую частоту на 
получим высоту для построения гистограммы.
Построив гистограмму мы получили аналог кривой распределения по которой можем выдвинуть гипотезу о законе распределения. Выровнять статистическое распределение с помощью закона о котором выдвинули гипотезу, для этого нужно статист. среднее m x* и статистическую дисперсию D x*.
Которые находим как
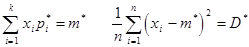
Естественной оценкой для мат. ожидания является среднее арифметическое значение:
.
Посмотрим, является ли эта оценка не смещенной, для этого найдем ее мате-матическое ожидание:
,
то есть оценка 
для m является несмещенной.
Найдем дисперсию этой оценки:
Эффективность или неэффективность оценки зависит от вида закона распределения случайной величины X. Если распределение нормально, то оценка 
для мат. ожидания m является и эффективной.
Перейдем к оценке для дисперсии D. На первый взгляд наиболее естественной представляется статистическая дисперсия D *, то есть среднее арифметическое квадратов отклонений значений Xi от среднего:
.
Проверим состоятельность этой оценки, выразив ее через среднее арифметическое квадратов наблюдений:
.
, где правая часть есть среднее арифметическое значений случайной величины X2 сходится по вероятности к ее мат. ожиданию: 
. Вторая часть сходится по вероятности к 
; вся величина сходится по вероятности к 
. Значит, оценка состоятельна.
Проверим ее на несмещенность, подставив в 
вместо 
его выражение и произведем действия:
.
Так как D* не зависит от выбора начала координат то отцентрируем все случайные величины 
. Тогда
.
Найдем мат. ожидание величины D*:
.
Но 
, 
, и получаем:
.
Отсюда видно, что величина D* не является несмещенной оценкой для дисперсии D; ее мат. ожидание не равно D, а несколько меньше. Пользуясь оценкой D* вместо D, будет проходить систематическая ошибка в меньшую сторону, чтобы ее ликвидировать введем поправку 
тогда мы получим несмещенную оценку для дисперсии:
При больших n поправочный коэффициент 
становится близким к единицы, и его применение теряет смысл. Поэтому в качестве приближенных значени (оценок) этих характеристик нужно взять:
,
.
Практическая часть
Упорядоченная выборка 
где n=100 количество замеров:
| 70.1 | 74.7 | 79.1 | 79.4 | 80.0 | 82.0 | 82.2 | 83.4 | 83.8 | 85.0 |
| 86.1 | 86.2 | 86.3 | 86.5 | 86.6 | 86.7 | 86.9 | 87.2 | 88.2 | 88.4 |
| 88.6 | 88.7 | 89.4 | 90.4 | 90.8 | 90.9 | 91.1 | 91.3 | 93.1 | 93.7 |
| 94.5 | 94.7 | 94.7 | 94.8 | 94.9 | 94.9 | 95.1 | 95.2 | 95.3 | 95.6 |
| 96.5 | 96.5 | 96.6 | 96.9 | 97.2 | 97.4 | 97.7 | 98.1 | 98.4 | 98.8 |
| 98.6 | 99.0 | 99.4 | 100.0 | 100.0 | 100.1 | 100.4 | 100.5 | 100.6 | 100.8 |
| 101.4 | 101.6 | 101.8 | 101.9 | 101.9 | 102.1 | 102.3 | 102.7 | 102.8 | 102.9 |
| 103.6 | 103.8 | 103.8 | 104.6 | 105.4 | 105.9 | 106.1 | 106.6 | 107.2 | 107.3 |
| 107.5 | 107.7 | 109.1 | 110.2 | 110.3 | 110.4 | 111.8 | 111.8 | 112.4 | 112.5 |
| 112.8 | 113.0 | 113.6 | 113.9 | 113.9 | 114.3 | 116.8 | 118.3 | 122.7 | 124.6 |
Размах выборки r=Xn-X1 =124.6-70.1= 54.5
На основе выше изложенной теории для исследования статистики составляем табл. 3.1.
Табл. 3.1
| Интервалы | Число попаданий в интервал | Частота попаданий в интервал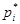 
| Высоты интервалов для гистограммы |
| 1. 70.10 - 75.55 2. 75.55 - 81.00 3. 81.00 - 86.45 4. 86.45 - 91.90 5. 91.90 - 97.35 6. 97.35 - 102.80 7. 102.80 - 108.25 8. 108.25 - 113.70 9. 113.70 - 119.15 10.119.15 - 124.60 | 23.5 13.5 | 0.020 0.030 0.080 0.150 0.170 0.235 0.135 0.110 0.050 0.020 | 0.0036697 0.0055045 0.0146788 0.0275229 0.0311926 0.0431192 0.0247706 0.0201834 0.0091743 0.0036697 |
| Сумма 1.000 |
По построенной гистограмме (рис. 3.1) можно предположить, что данное распределение подчиняется нормальному закону. Для подтверждения выдвинутой гипотезы проведем оценку неизвестных параметров, для мат. ожидания
,
для оценки дисперсии
.
Полагая в выражении нормальной плотности
, где 
и пользуясь, либо приложением 4 в учебнике Вентцель Е.С., Овчаров Л.А.” Прикладные задачи теории вероятностей.” - М.: Радио и связь, 1983, либо как в нашем случае воспользоваться системой MathCad, получим значения на границах разрядов табл. 3.2:
Табл. 3.2
| x | f(x) |
| 1. 70.10 2. 75.55 3. 81.00 4. 86.45 5. 91.90 6. 97.35 7. 102.80 8. 108.25 9. 113.70 10.119.15 11.124.60 | 0.0010445 0.0036354 0.0097032 0.0198601 0.0311717 0.0375190 0.0346300 0.0245113 0.0133043 0.0055377 0.0017676 |
и построим выравнивающую ее нормальную кривую рис. 3.1
Рассчитаем вероятность (табл. 3.3) попадания с. в. Х в k -й интервал по формуле
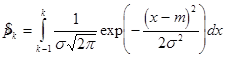
Табл. 3.3
| 
|
| 1. 70.10 - 75.55 2. 75.55 - 81.00 3. 81.00 - 86.45 4. 86.45 - 91.90 5. 91.90 - 97.35 6. 97.35 - 102.80 7. 102.80 - 108.25 8. 108.25 - 113.70 9. 113.70 - 119.15 10.119.15 - 124.60 | 0.0115694 0.0344280 0.0790016 0.1398089 0.1908301 0.2009057 0.1631453 0.1021833 0.0493603 0.0183874 |
Для проверки правдоподобия гипотезы воспользуемся критерием согласия 
для этого возьмем данные из табл. 3.1 и 3.3 и подставим в формулу:
Рис. 3.1
Определяем число степеней свободы (10-1- l)=7, где l - число независимых условий (количество параметров подлежащих оценки в нашем случаи их l= 2, это mx, Dx - для нормального распределения). По приложению 3 в учебнике Вентцель Е.С., Овчаров Л.А. ”Теория вероятностей и ее инженерные приложения.” - М.: Наука, 1988 находим при r=7, p=0.95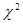 
=2.17 для уровня значимости 
и видим, что 
, но даже меньше.
Это свидетельствует о том, что выдвинутая нами гипотеза о нормальности распределения не противоречит опытным данным.