Механизмы, о которых пойдет речь в уроке, называют «простыми ». Их изобрели еще в глубокой древности и продолжают пользоваться до сих пор (см. рис. 7)
Рис. 7. Принцип действия простых механизмов
Действия этих механизмов основаны на простых механических принципах.
Соединив вместе несколько простых механизмов, можно получить сложный механизм (см. рис. 8)
Рис. 8. Сложный механизм
По сравнению с простыми, сложные механизмы работают более эффективно и позволяют решать более сложные инженерные задачи.
Может ли человек поднять дом? Дом слишком тяжелый, не получится (см. рис. 9)
Рис. 9. Поднятие дома
Но что, если мы разберем его на кирпичи? Конечно, можно сказать, что это будет не совсем дом, но нам важно то, что теперь эта задача человеку под силу. Правда, это займёт больше времени (см. рис. 10)
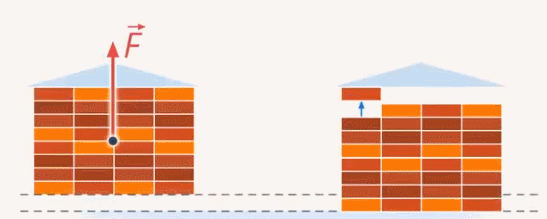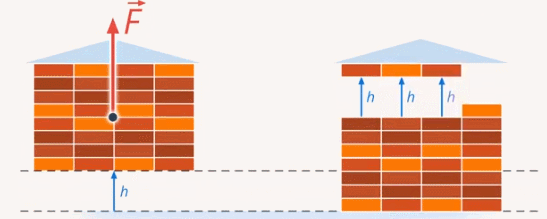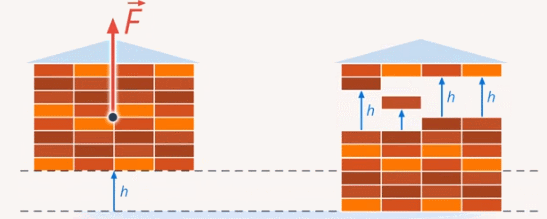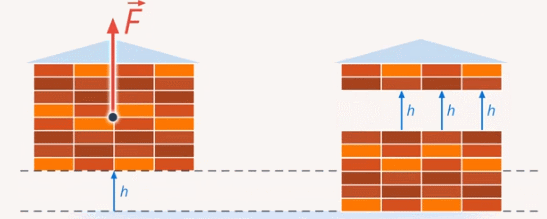
Рис. 10. Выполнение одной и той же работы
При этом работа будет та же, что и в случае, если бы человек поднимал дом целиком: массу m поднимают на высоту h:
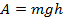
Получается, возможности человека безграничны, ведь по одному кирпичу можно перенести любой дом, каким бы огромным он ни был? На самом деле, нет – чем больше масса дома (больше кирпичей надо перенести), тем больше времени это займёт.
Можно уменьшить силу, которую мы прикладываем за один подход, но при этом увеличится путь и время подъема. Совершенная работа, или затраченная энергия, при этом останется такой же:
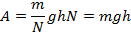
Это общий принцип действия большинства простых механизмов: выигрывая с их помощью в прикладываемой силе, мы будем проигрывать в расстоянии, которое нужно будет преодолеть (можно взбираться на гору по прямой – получится быстро, но тяжело, а можно – по серпантину – легче, но дольше – (см. рис. 11))
Рис. 11. Общий принцип простых механизмов
Наклонная плоскость
Если друг попросит затащить его вместе с санками на горку, вы, вероятно, сможете это сделать. А смогли бы вы просто поднять друга вместе санками на высоту горки (см. рис. 12)
Рис. 12. Наклонная плоскость
Вряд ли.
В первом случае вы поднимаете санки по склону, во втором – вертикально вверх. В данной ситуации склон является примером простейшего механизма – наклонной плоскости.
Ею часто пользуются грузчики, когда нужно поднять груз на некоторую высоту. Наклонная плоскость позволяет поднять груз, прикладывая меньшую силу. И чем меньше наклон, тем меньше потребуется сила (см. рис. 13)
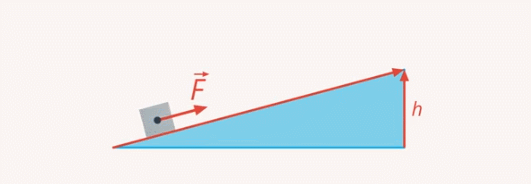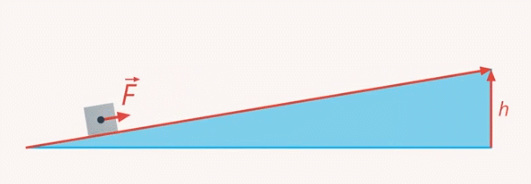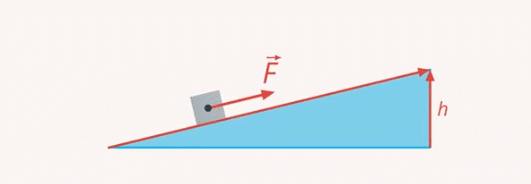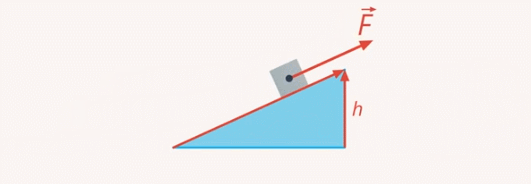
Рис. 13. Использование наклонной плоскости
Любой, кто катался на санках, это знает: по крутому склону поднимать их наверх намного тяжелее, чем по пологому. Но, используя наклонную плоскость, нужно преодолеть большее расстояние. Длина склона всегда больше высоты горки (см. рис. 14)
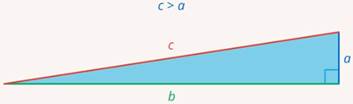
Рис. 14. Длина склона всегда больше высоты горки
На математическом языке это звучит так: в прямоугольном треугольнике гипотенуза всегда больше катета.
Итак, можно сказать, что наклонная плоскость даёт выигрыш в силе, но проигрыш в расстоянии. Чем меньше угол наклона, тем больше выигрыш в силе.
Выигрыш-проигрыш
Наклонная плоскость чаще всего используется для подъёма грузов. Конечно, это можно сделать и без неё – поднять груз равномерно, прикладывая силу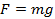 
(см. рис. 15)
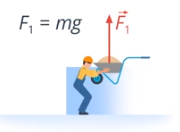
Рис. 15. Приложенная сила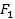 
Но наклонная плоскость позволяет поднять тот же груз, но приложить при этом меньшую силу (см. рис. 16)
Рис. 16. Прикладывание меньшей силы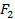 
Поскольку нам это выгодно, так и скажем: «мы выиграли в силе». Можно даже указать, во сколько раз меньше получилась сила. Например, «выигрыш в силе в 3 раза» значит, что вместо силы 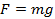, нам достаточно приложить силу в 3 раза меньше: 
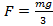. При этом мы поднимем тот же груз массой m.
Итак, если нам выгодно изменение физической величины, мы говорим о «выигрыше». Ну, а если невыгодно – то о «проигрыше».
Винт
Если свернуть наклонную плоскость (см. рис. 17), то получится ее частный случай – винт!
Рис. 17. Винт
Принцип действия винта рассмотрим на примере шурупа. Вкрутить его легче, чем вбить гвоздь такой же длины.
Если перейти в систему отсчёта, связанную с гвоздём, то стенка относительно гвоздя поднимается вертикально вверх (см. рис. 18)
Рис. 18. Гвоздь и шуруп
А в системе отсчёта, связанной с шурупом, стенка поднимается по шурупу как по спирали (по свёрнутой наклонной плоскости).
За счёт этого получается выигрыш в силе. Но при этом увеличивается пройденный путь. В примере с санками и горкой мы проходили больший путь вдоль плоскости, а здесь мы делаем несколько оборотов отверткой. Точки шурупа проделывают больший путь, чем точки гвоздя.
Клин
Рассмотрим еще один инструмент: топор. Во время первого удара по бревну, топор прорезает его. Тут действует принцип ножа: небольшая площадь, большое давление (см. рис. 19)
Рис. 19. Принцип ножа
Но дальше мы бьём уже по-другому (см. рис. 20)
Рис. 20. Работа топором
Что происходит? Древесина движется вдоль лезвия топора (наклонной плоскости). На нее действует сила реакции опоры перпендикулярно поверхности лезвия (см. рис. 21), и под ее действием древесина раскалывается
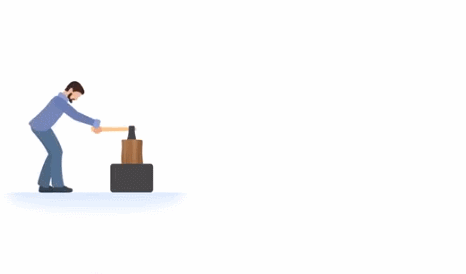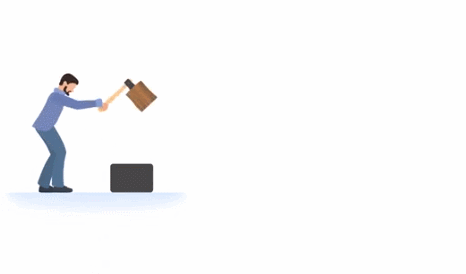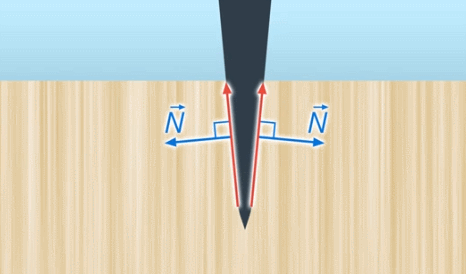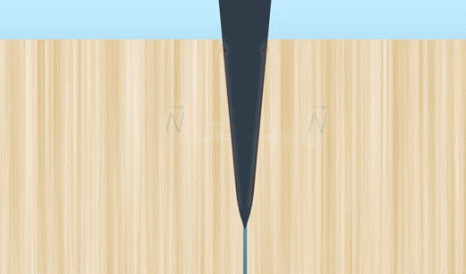
Рис. 21. Клин
Топор является примером ещё одного частного случая наклонной плоскости, который называют клином. И снова получаем выигрыш в силе и проигрыш в перемещении – топор вгоняется в бревно на несколько сантиметров, чтобы разъединить его на несколько миллиметров.
Про все виды наклонной плоскости мы можем сказать, что они дают выигрыш в силе. И чем меньше угол у основания плоскости, тем больше этот выигрыш (см. рис. 13) Известных нам математических инструментов пока не хватает, чтобы точно рассчитать этот выигрыш, но чуть позже мы научимся это делать.
Рычаг
Рассмотрим второй из выделенных нами типов простых механизмов.
Представьте: папа сел на качели (см. рис. 22)
Рис. 22. Качели с человеком
Чтобы его уравновесить, вы сядете на качели подальше от центра (см. рис. 23)
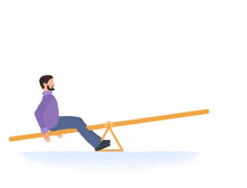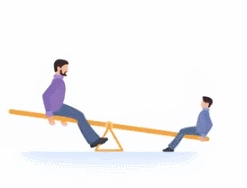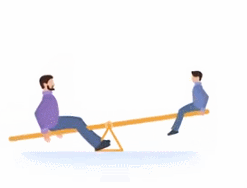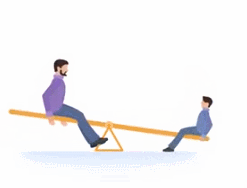
Рис. 23. Уравновешивание качелей
Так вы, давя на качели меньшим весом, уравновесите более тяжелого папу.
Подсознательно вы использовали принцип действия простого механизма – рычага. Рычаг – это твердое тело, которое имеет точку опору и может вращаться вокруг неё. Свойствами рычага мы пользуемся, когда толкаем дверь дальше от петель, чтобы её открыть; когда берём лопату поближе к концу черенка и т.д (см. рис. 24)
Рис. 24. Принцип рычага
Чтобы строго сформулировать используемые нами свойства рычага, введём несколько понятий.
У качелей есть точка, которая остается неподвижной и вокруг которой они вращаются (см. рис. 25)
Рис. 25. Точка опоры
Эта точка называется точкой опоры (в ней качели крепятся к опоре). Для лопаты точкой опоры будет точка (см. рис. 26), для ножниц – винтик и т.д.
Рис. 26. Точка опоры для лопаты и ножниц
Итак, у любого рычага есть одна неподвижная точка, которая называется точкой опоры.
Какие силы действуют на качели (см. рис. 27)?
Рис. 27. Качели
1) В точке опоры действует сила реакции опоры. Из-за этого данная точка остаётся неподвижной (см. рис. 28)
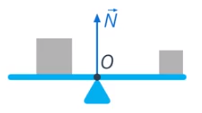
Рис. 28. Сила реакции опоры
2) Папа действует на качели своим весом. Эта сила стремится вращать качели против часовой стрелки (см. рис. 29)
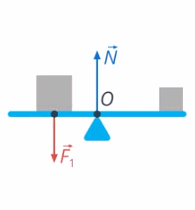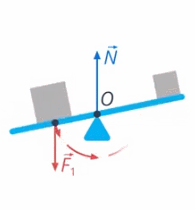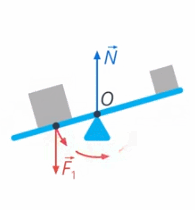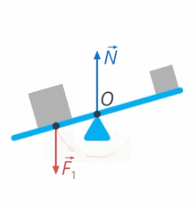
Рис. 29. Вес человека
3) Вы тоже действуете на качели своим весом. Эта сила вращает качели по часовой стрелке (см. рис. 30)
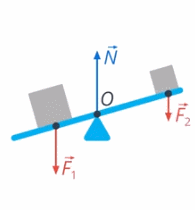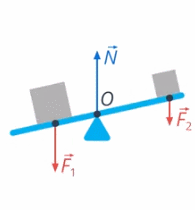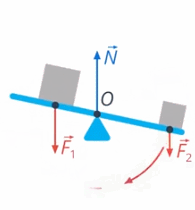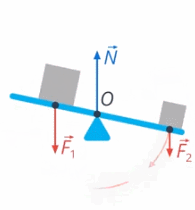
Рис. 30. Вес второго человека
Если использовать для рычага модель материальной точки, то получится, что все силы, которые мы описали, действуют вдоль вертикали (вверх или вниз) (см. рис. 31)
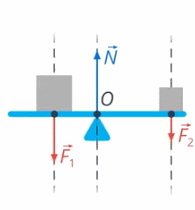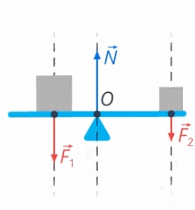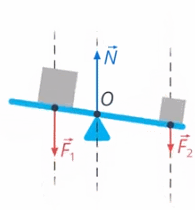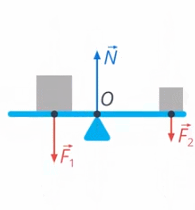
Рис. 31. Модель материальной точки
Тогда движение рычага было бы возможно только вверх или вниз. Но рычаг вращается, значит, модель материальной точки для его описания неприменима.
Поэтому рассмотрим не только силы, действующие на рычаг, но и точки их приложения. Все знают, насколько труднее удерживать груз на вытянутой руке, чем на согнутой (см. рис. 32)
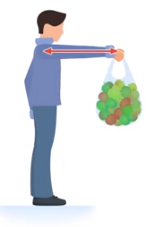
Рис. 32. Удерживание груза на вытянутой и согнутой руке
Можно сделать предположение, что чем ближе точка приложения силы к точке опоры, тем меньше её «вклад» в поворот рычага.
Чтобы определять точку приложения силы, введем понятие плеча силы (по аналогии с плечом руки, которая удерживает груз).
Плечо силы – это минимальное расстояние от заданной точки до прямой, вдоль которой действует сила (см. рис. 33)
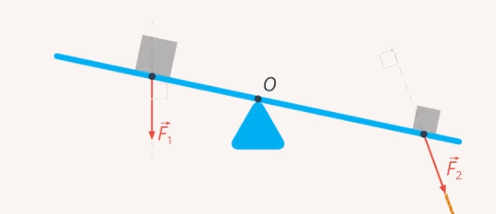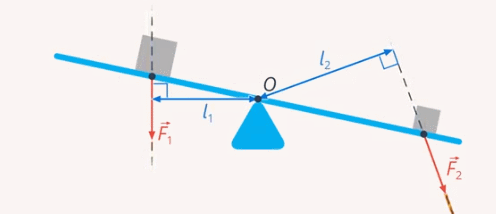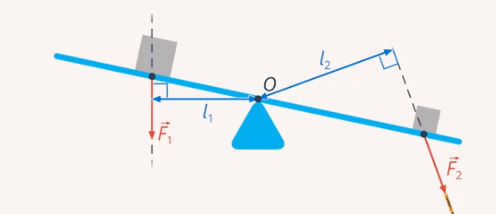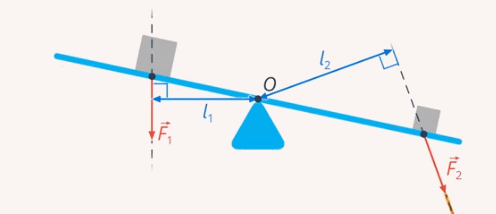
Рис. 33. Плечо силы
В геометрии мы определили такое расстояние, как перпендикуляр, опущенный из точки опоры на прямую, вдоль которой действует сила.
Чаще всего мы будем рассматривать силы, действующие перпендикулярно рычагу, и плечо силы будет равно расстоянию от точки опоры до точки приложения силы (см. рис. 34)
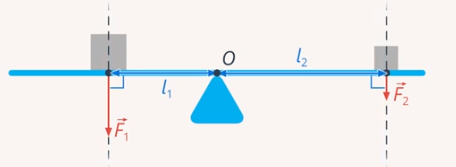
Рис. 34. Силы, действующие перпендикулярно рычагу
Вращение рычага зависит и от значения силы, и от ее плеча – чем больше сила и длиннее её плечо, тем сильнее будет вращающее действие этой силы (см. рис. 35)
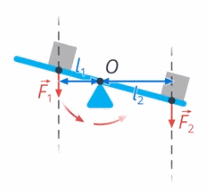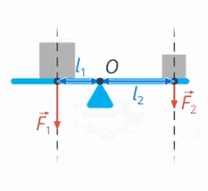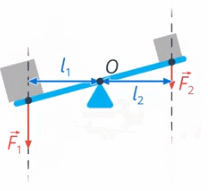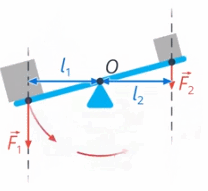
Рис. 35. Вращение рычага
Назовем произведение силы на ее плечо моментом силы.
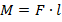
Вспомним, что тело сохраняет свою скорость, если действующие на него силы уравновешены. При вращении тела, то же самое можно сказать про момент силы: если моменты сил уравновешены, то тело вращается равномерно или остается в покое (см. рис. 36)
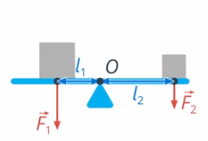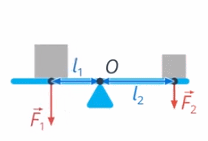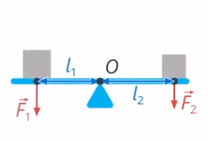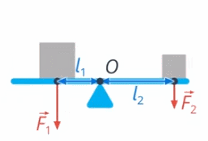
Рис. 36. Моменты сил уравновешены
Вернёмся к примеру с качелями (см. рис. 23): чтобы они уравновесились, моменты двух сил – вашего и папиного веса – также должны быть уравновешены. Момент силы реакции опоры не учитываем: он равен нулю, поскольку плечо этой силы равно нулю (см. рис. 37)
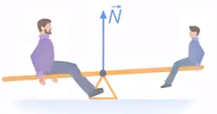
Рис. 37. Момент силы реакции опоры равен 0
Момент веса папы (см. рис. 38):
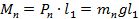
Момент вашего веса (см. рис. 38):
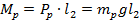
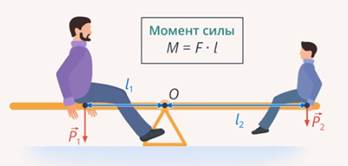
Рис. 38. Моменты силы
Тогда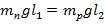 
. Теперь видно: чем больше будет 
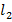, тем меньшего достаточно веса 
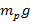. Поэтому, если длина качелей будет достаточной, чтобы взяться подальше от точки опоры, взрослого человека легко уравновесить рукой (см. рис. 39)
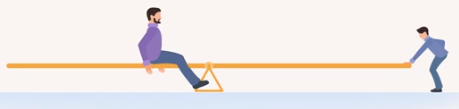
Рис. 39. Достаточная длина качелей
Простые механизмы, работающие по тому же принципу, что и качели, называют рычагами. Примерами рычагов, как мы уже сказали, являются лопата, тачка, плоскогубцы (см. рис. 40)
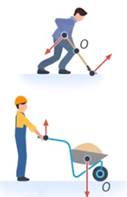
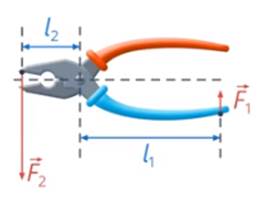
Рис. 40. Примеры рычагов
На примере качелей мы увидели, что с помощью рычага можно получить выигрыш в силе, если увеличить плечо. Вокруг себя вы можете увидеть множество аналогичных примеров:
- дверь вы открываете ближе к краю, а не к петлям: плечо больше, значит, можно прикладывать меньшую силу (см. рис. 41)
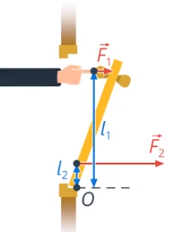
Рис. 41. Открывание двери
- у дверной ручки тоже есть своё плечо, чтобы проще было её поворачивать. А вот круглые ручки поворачивать сложнее (см. рис. 42)
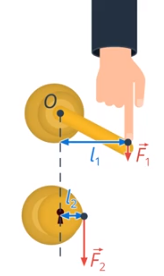
Рис. 42. Дверная ручка