Математическая модель пространственного движения управляемой парашютно-тросовой системы типа «ветролет»
В. М. Чуркин, доктор физико-математических наук, Московский авиационный институт (Национальный исследовательский университет), Москва, Россия
Т. Ю. Чуркина, кандидат технических наук, Московский авиационный институт (Национальный исследовательский университет), Москва, Россия
А. М. Гирин, кандидат технических наук, Московский авиационный институт (Национальный исследовательский университет), Москва, Россия
Замечание (рец. 1)
На рисунке непонятно, где располагается место соединения троса с основным парашютом, показать.
Пожелание (рец. 2)
Показать действенность модели числовым примером, графиком, согласованием с экспериментом, возможно, взятыми из других источников.
Описывается математическое моделирование пространственного движения управляемой парашютно-тросовой системы типа «ветролет». Рассматриваемая система представляется моделью, составленной из основного парашюта и тормозного парашюта, соединенных тросом. Основной парашют считается твердым телом, имеющим две плоскости симметрии, а тормозной парашют – осесимметричным твердым телом. Трос рассматривается как абсолютно гибкая упругая нить, соединенная идеальными шарнирами с основным и тормозным парашютами. Управление основным парашютом осуществляется путем изменения длины управляющих строп, вызывающего деформацию купола и, как следствие, изменение его аэродинамики. При одновременном изменении длины управляющих строп происходит маневрирование основного парашюта в вертикальной плоскости, а при изменении длины управляющих строп с заданной разностью хода – пространственное маневрирование основного парашюта. Составляется система динамических и кинематических уравнений пространственного движения основного парашюта, тормозного парашюта и троса. В случаях, когда основной и тормозной парашюты соединены тросом, массой которого и приложенными к нему силами пренебречь нельзя, его движение представляется уравнениями движения абсолютно гибкой упругой нити в проекциях на оси естественного трехгранника. В результате предлагаемая математическая модель представляется системой обыкновенных дифференциальных уравнений и дифференциальных уравнений в частных производных, для решения которых могут быть использованы различные численные методы или комплексный численно-аналитический подход. Например, при решении методом характеристик аналитическая часть исследования включает нахождение характеристик и запись соответствующих характеристических уравнений с последующим их численным интегрированием.
Ключевые слова: математическая модель, парашютно-тросовая система, управляемый парашют, аэродинамика купола, сила натяжения троса.
Введение
Актуальной проблемой является десантирование полезного груза с точной доставкой в необходимое место земной поверхности и разработка технических решений для этого [1]. Это, например, связано с быстрейшим временем оказания помощи пострадавшим, ликвидацией лесных пожаров в труднодоступных районах, а также с риском потери ценного десантируемого оборудования. Задача регулируемого спуска парашютов различной конфигурации решалась, например, в [2–5]. Еще одна актуальная тема – расчет параметров, необходимых для мягкой посадки спускаемых космических аппаратов (КА) (например, Чуркин В. М., Чуркина Т. Ю. «Математическая модель движения космического аппарата с комбинированной системой мягкой посадки»), или вывода на орбиту аппаратов с помощью тросовых систем [6]. И даже удаление отработавших свой ресурс КА с низких орбит с приземлением в безопасную точку земной поверхности. Одним из технически возможных способов решения такой задачи может быть применение парашютно-тросовой системы (ПТС) типа «ветролет», состоящей из основного парашюта и соединенного с ним тросом тормозного парашюта.
Цель исследования – создание относительно простой математической модели, позволяющей определять траекторию движения ПТС, следовательно, и груза.
Построение математической модели управляемого пространственного движения ПТС типа «ветролет»
Существуют различные подходы моделирования и исследования движения парашютных систем или движения связанных тел [7–9].
Задача о математическом моделировании и исследовании динамики плоского движения ПТС типа ветролет решалась в работе [10], на основании которой построим математическую модель пространственного движения подобной ПТС. Условимся считать основной парашют твердым телом, имеющим две плоскости симметрии, его коуш – идеальным шарниром, трос – абсолютно гибкой невесомой нитью, а тормозной парашют – осесимметричным твердым телом. Допустим, что коуш основного парашюта – центр давления купола – и центр масс лежат на линии пересечения плоскостей его симметрии. Центр давления и центр масс тормозного парашюта лежат в одной точке, расположенной на оси симметрии парашюта, скорость набегающего потока – горизонтальный вектор, модуль которого зависит только от высоты Н, а изменения плотности атмосферы ρ от высоты Н пренебрежимо малы. Управление основным парашютом осуществляется путем изменения длины строп управления, вызывающего деформацию купола и, как следствие, изменение его аэродинамики. При одновременном изменении длины строп управления на величину δ происходит маневрирование основного парашюта в вертикальной плоскости, а при изменении длины строп с разностью хода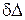 
– пространственное маневрирование основного парашюта.
Для моделирования пространственного движения ПТС (см. рисунок) используются следующие системы координат: абсолютная система XOYZ; система X 1 O 1 Y 1 Z 1, связанная с основным парашютом; система X 2 O 2 Y 2 Z 2, связанная с тросом; система X 3 O 3 Y 3 Z 3, связанная с тормозным парашютом.
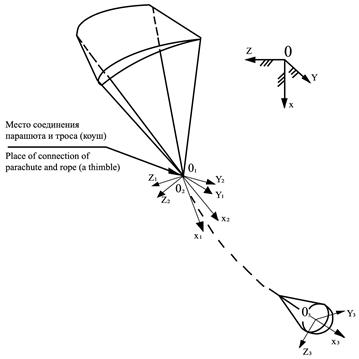
Схема парашютно-тросовой системы типа «ветролет»
Parachute-rope system scheme of the type of a flying machine
Начало системы X 1 O 1 Y 1 Z 1 совместим с коушем основного парашюта, а ось О 1 Х 1 направим вдоль линии пересечения плоскостей симметрии. Начало системы X 2 O 2 Y 2 Z 2 также совместим с коушем основного парашюта, а ось O 2 X 2 направим вдоль прямой, соединяющей точку O 2 с коушем тормозного парашюта. Начало системы X 3 O 3 Y 3 Z 3 расположим в центре масс тормозного парашюта, а ось его симметрии выберем в качестве оси O 3 X 3.
Динамические уравнения ОП в проекциях на оси системы X 1 O 1 Y 1 Z 1 запишем в виде
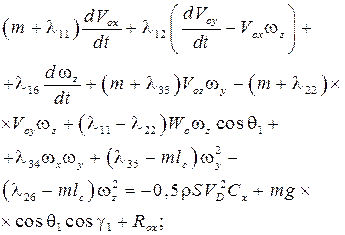
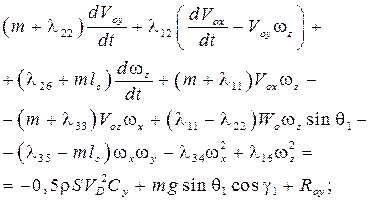
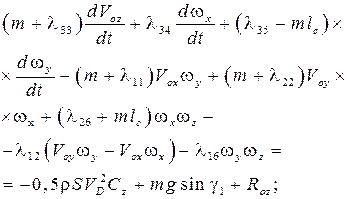
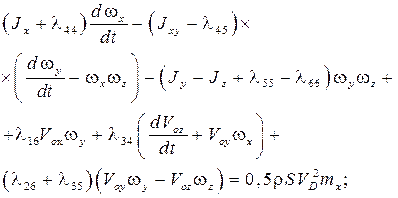
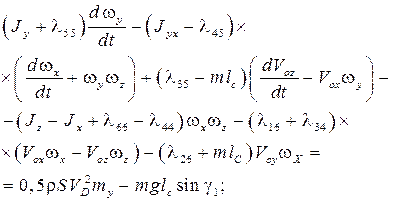
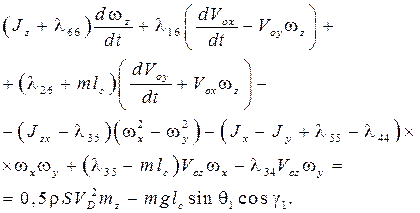
(1)
Здесь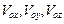 
– проекции вектора скорости коуша основного парашюта; 
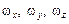– проекции вектора угловой скорости вращения основного пара; 
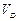– скорость центра давления купола 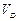относительно набегающего потока;
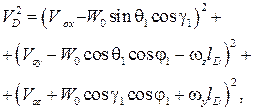
где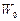 
– скорость ветра на высоте H 0 коуша основного парашюта; m – масса основного парашюта; 
– осевые и центробежные моменты инерции основного парашюта относительно осей связанной системы координат; 
– коэффициенты присоединенных масс купола основного парашюта;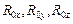 
– проекции вектора силы натяжения троса в коуше основного парашюта;
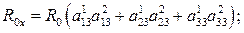
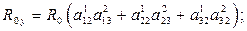
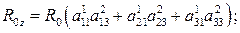
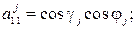
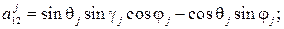
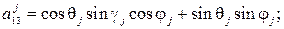
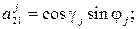
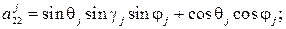
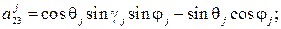
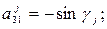
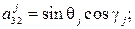
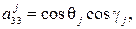
где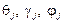 
– углы поворота основного парашюта относительно осей систем 
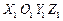при j = 1) и 
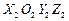при j = 2; 
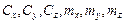– коэффициенты аэродинамических сил и моментов купола основного парашюта;
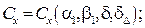
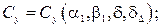
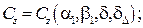
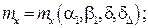
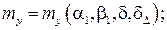
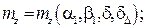
α1, β1 – углы атаки и скольжения купола основного парашюта;
;
,
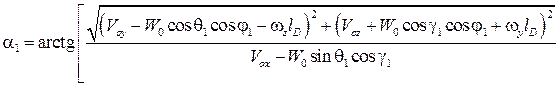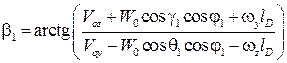где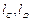 
– расстояния от коуша до центра масс и центра давления купола основного парашюта соответственно; 
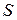– характерная площадь купола основного парашюта; 
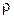– плотность воздуха.
При проведении пробных расчетов по моделированию пространственного движения спускаемого объекта с управляемым парашютом для коэффициентов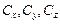 
использовались зависимости, имеющие следующую структуру:
.
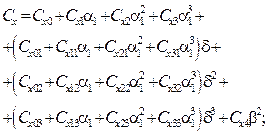
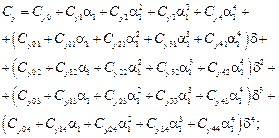
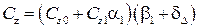Для тормозного парашюта динамические уравнения в проекциях на оси системы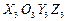 
представим следующим образом:
.
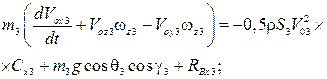
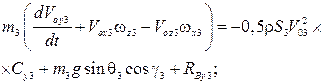
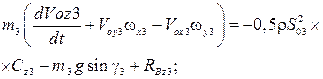
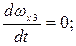
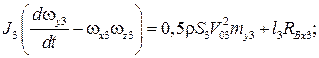
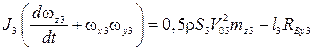(2)
Здесь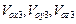 
– проекции вектора скорости центра масс ТП; 
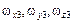– проекции вектора угловой скорости вращения ТП; 
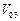– скорость центра масс ТП относительно набегающего потока
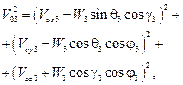
где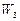 
– скорость ветра на высоте 
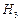центра масс ТП; 
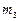– масса ТП; 
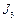– момент инерции ТП относительно осе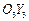й 
и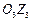 
; 
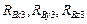– проекции вектора силы натяжения троса в коуше ТП,
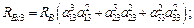
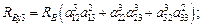
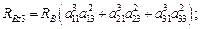
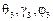– углы поворота ТП относительно системы; 
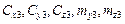– коэффициенты аэродинамических сил и моментов ТП,
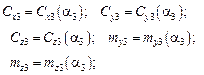
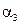– угол атаки ТП,
;
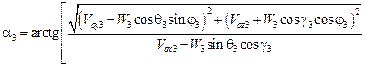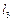– расстояние от коуша ТП до его центра масс; 
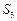– характерная площадь купола ТП.
Динамические уравнения (1) и (2) дополняем следующими кинематическими уравнениями:
, 
.
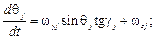
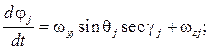
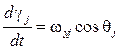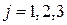(3)
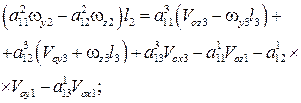
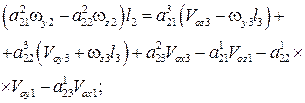
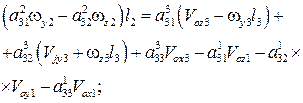
(4)
,
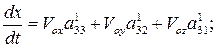
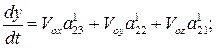
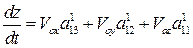(5)
где ;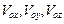 
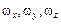– проекции на оси системы 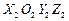вектора скорости коуша основного парашюта и вектора угловой скорости вращение основного парашюта соответственно; 
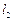– расстояние между коушами основного парашюта и тормозного парашюта; 
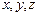– координаты коуша основного парашюта в системе 
.
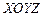В случаях, когда основной и тормозной парашюты соединены длинным тросом, массой которого и приложенными к нему силами пренебречь нельзя, уравнения движения основного и тормозного парашютов дополняются уравнениями движения троса, в качестве которых можно использовать уравнения движения абсолютно гибкой упругой нити, записанные в проекциях на оси естественного трехгранника:
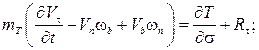
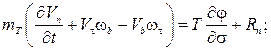
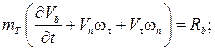
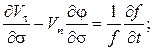
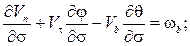
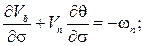
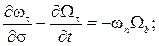
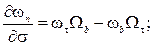
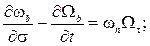
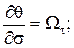
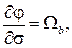
(6)
где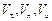 
– проекции вектора абсолютной скорости элемента троса; 
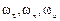– проекции вектора абсолютной угловой скорости элемента троса; 
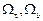– проекции вектора Дарбу; σ – дуговая координата элемента троса; 
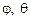– углы кривизны и кручения троса; T – сила натяжения троса; 
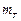– линейная плотность растянутого троса; f – коэффициент растяжения троса,
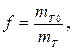
где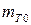 
– линейная плотность нерастянутого троса; 
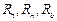– проекции вектора равнодействующей внешних сил, приложенных к тросу.
Если растяжение троса подчиняется закону Гука, то
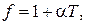
где α – удельное относительное удлинение троса,
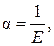
где E – модуль упругости троса.
Уравнения системы (6) должны решаться при граничных условиях, которыми служат уравнения системы (1) при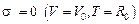 
и уравнения системы (3) при 
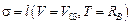, где l – длина троса.
Выводы
1. В работе построена математическая модель пространственного движения ПТС с учетом уравнений движения троса в виде систем нелинейных обыкновенных дифференциальных уравнений и уравнений в частных производных.
2. Составленные системы динамических и кинематических уравнений пространственного движения управляемой ПТС позволяют оценивать основные динамические характеристики проектируемых ПТС и рассчитывать их конструктивные параметры
3. Полученные результаты могут быть использованы для определения параметров мягкой посадки спускаемых космических аппаратов и авиационных парашютных систем, расчета работоспособности элементов конструкции ПТС с учетом динамики нагружения [11].
4. Следует отметить, что наибольшие трудности вызывает исследование движения троса. Решению этой задачи посвящено большое число публикаций как отечественных, так и зарубежных авторов. Причем такая задача возникает при исследовании движения троса в различных средах, и не только для ПТС [12–16]. Расчет тросовых систем, предлагаемых к использованию при спуске отработавших ресурс КА и даже в зеленых энергетических системах [17–20], где излагаются различные методы численного решения уравнений движения троса. Аналитический анализ динамики тросовых систем основан либо на линеаризации уравнений движения троса, либо на их предельном упрощении и замене уравнениями модельных задач математической физики. В ряде работ предлагается использовать комплексный численно- аналитический подход. Наибольшее распространение получил метод характеристик, в котором аналитическая часть исследования включает нахождение характеристик и запись соответствующих характеристических уравнений, а их интегрирование выполняется на ЭВМ.