Определение координат центра тяжести плоской фигуры.
Способы определения координат центра тяжести
1 Аналитический (путем интегрирования).
2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
3 Экспериментальный (метод подвешивания тела).
4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1 + S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны

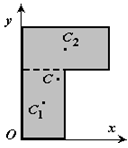
Рисунок 1.8
5 Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):


Центры тяжести простейших фигур

Центр тяжести треугольника
Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок а).
DM = MB, CM = (1/3) AM.
Центр тяжести дуги окружности
Дуга имеет ось симметрии (рисунок б). Центр тяжести лежит на этой оси, т.е. yC = 0.


следовательно:

Центр тяжести кругового сектора
Сектор радиуса R с центральным углом 2 α имеет ось симметрии Ox, на которой находится центр тяжести (рисунок в).
Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса (2/3) R.
Центр тяжести сектора совпадает с центром тяжести дуги AB:

Пример
Определить координаты центра тяжести плоской фигуры, изображённой на рис. № 1 при следующих данных: а=40 см, b=100 см, r=20 см.
Решение. Фигура разбивается на три простейшие части: прямоугольник, треугольник, полукруг, площади которых соответственно равны
 см2,
см2,  см2,
см2,  см2.
см2.
Площадь всей фигуры
 см2.
см2.

Рис. №1
Центры тяжестей рассматриваемых частей фигуры имеют следующие координаты:
для прямоугольника х1=30 см, y1=20 см;
для треугольника х2=60+40/3=73,3 см, y2=40/3=13,3 см;
для полукруга х3=40 см, y3=40-4·20/(3·π)=31,5 см.
Координаты центра тяжести фигуры в целом вычисляются по формулам
 см;
см;
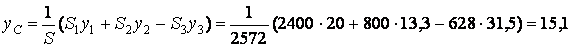 см.
см.
Ответ: xC = 41 см, yC = 15,1 см.
Практическая работа № 6.
Решение задач динамики методом кинематики.
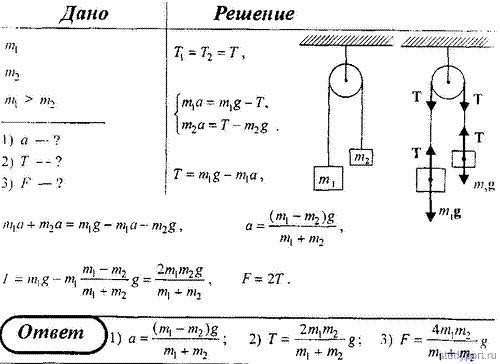
Пример решения
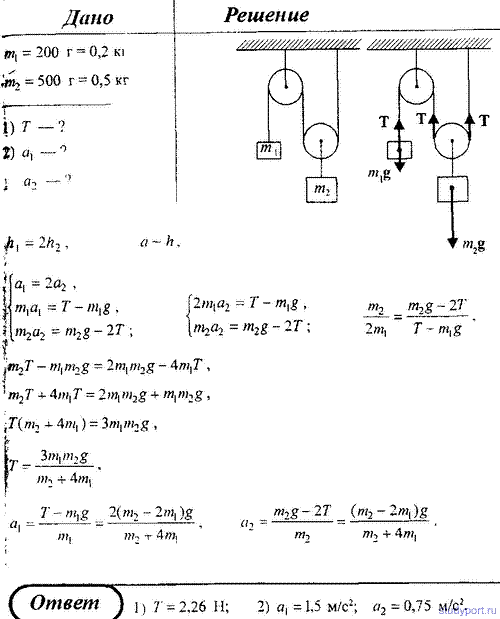
Простейшая машина Аттвуда, применяется для изучения закона равноускоренного движения, представляет собой два груза с не равными массами m1 и m2 (например m1 > m2), которые подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определить: 1) ускорение грузов; 2) силу натяжения T; 3) силу F, действующую на ось блока.
На рисунке изображена система блоков, к которым подвешены грузы массами m1 = 200 г и m2 = 500 г. Считая, что груз m1поднимается, а подвижный блок с m2 опускается, нить и блок невесомы, силы трения отсутствуют, определить: 1) силу натяжения нити Т; 2) ускорение, с которыми движутся грузы.