Расчеты стержней испытывающих деформацию растяжения (сжатия).
Ступенчатый стержень круглого поперечного сечения нагружен силами 
. Принимаем материал стержня МА1, 
, 
, 
.
Решение:
1.Построим эпюры продольных сил.
Схема нагружения стержня представлена на рисунке. Обозначим сечения, в которых приложены силы и меняются размеры стержня буквами, начиная от А до F. Сечениями, где приложены силы, стержень разбивается на три участка, в пределах которых продольная сила постоянная, поэтому для определения ее значений нужно рассечь каждый участок и из условия равновесия отсеченной части, не содержащей заделку, определить величину продольной силы.
Проведем на участке АВ произвольное сечение I-I, отбросим часть стержня, содержащую заделку, и рассмотрим условие равновесия оставшейся правой части. На рассматриваемую часть стержня действует сила Р3 = 20кН и продольная сила N1 в сечении I-I. При определении продольных сил в сечениях предполагаем, что они растягивают рассматриваемую часть стержня, т.е. направлены от сечения.
Проектируя силы на ось Х, получим N1 - Р3 = 0. Откуда N1 =Р3 =20 кН.
Т.к. продольная сила N1 получилась с положительным знаком, то участок стержня АВ растягивается.
Проведем произвольное сечение II-II и рассмотрим равновесие отсеченной части стержня, не содержащей заделку.
,
N2 +Р2 - Р3 = 0
N2 = -Р2 + Р3 =20 -10 = 10 кН.
Положительный знак продольной силы N2 свидетельствует о том, что третий участок испытывает растяжение.
Проведем произвольное сечение III-III и рассмотрим равновесие отсеченной части стержня, не содержащей заделку.
,
N3 - Р1 +Р2 - Р3 = 0
N3 = Р1 - Р2 + Р3 =40 - 10 + 20 = 50 кН.
Положительный знак продольной силы N3 свидетельствует о том, что третий участок испытывает растяжение.
|
|
По найденным значениям продольных сил строим график (эпюру) изменения продольных сил по длине стержня. Проводим базу эпюры параллельно оси стержня и в выбранном масштабе откладываем вверх положительные значения продольных сил и вниз отрицательные.
При правильно построенной эпюре продольных сил в сечениях, где приложены сосредоточенные силы на эпюре будут иметь место скачки на величину приложенной силы.
2 Определим необходимые размеры попречных сечений бруса.
Необходимые размеры поперечних сечений бруса определим исходя из условии прочности при растяжении.
Определим площади сечений на каждом участке
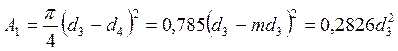
Значение напряжений на каждом участке
Выразим диаметр на участке где продольные силы имеют большее значение.
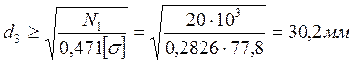
Округляем диаметры до ближайшего целого большего числа.
2 Построение епюр нормальних напряжений
По этим данным строим эпюру нормальных напряжений
3.Построение эпюры перемещений поперечных сечений.
Деформация бруса на каждом участке
Перемещения в сечениях
4.Определим необходимую толщину и диаметр головки стержня
На срез ось рассчитываем по формуле
Принимаем D=41мм
На смятие ось рассчитываем по формуле
Принимаем h=8мм
Практическая работа № 8.
Расчеты при изгибе.
Для балки, изображенной на рис.6.20 построить эпюры поперечной силы Qy и изгибающего момента Mx и определить опасное сечение. Пусть величины P = 10 кН, a = 2 м, b = 3 м.
Решение.
Определим реакции опор. Запишем уравнения равновесия статики. Из этих уравнений получим:
|
|
кН.
кН.
Для проверки правильности определения реакции опор используем уравнение:
; 
.
6 – 10 + 4 = 0,
0 º 0.
Рис.6.20
Значит, реакции определены правильно.
Определим внутренние усилия, возникающие в материале балки. Следует рассмотреть два участка, границами участков являются точки приложения сосредоточенной силы Р и опорных реакций RA и RB. Обозначим границы участков буквами А, С и В.
Рассечем первый участок АС.
Отбросим правую часть, т.к. она сложнее.
Заменим отброшенную часть внутренними усилиями Qy и Mx.
Уравновесим отсеченную часть, запишем уравнения равновесия:
Вычислим Qy и Mx в граничных точках участка:
при z1 = 0, Qy1 = RA = 6 кН, Mx1 = 0;
при z1 = а = 2 м, Qy1 = RA = 6 кН, Mx1 = 12 кНм.
Рассмотрим второй участок СВ. Рассечем его и отбросим левую часть, заменим её внутренними силами. Из уравнений равновесия получим
Вычислим Qy и Mx в граничных точках участка:
при z2 = 0, Qy2 = - RВ = - 4 кН, Mx2 = 0;
при z2 = а = 3 м, Qy2 = - RВ = - 4 кН, Mx2 = 12 кНм.
Построим эпюры Qy и Mx.
По полученным эпюрам определим опасное сечение, оно проходит через точку приложения силы P, так как Mx достигает там наибольшего значения.
Практическая работа № 9
Расчеты при кручении.
К стальному валу постоянного поперечного сечения (рис. 3.8) приложены четыре внешних скручивающих момента: 
кН·м; 
кН·м; 
кН·м; 
кН·м. Длины участков стержня: 
м; 
м, 
м, 
м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при 
кН/см2 и построить эпюру углов закручивания поперечных сечений стержня.
