Лабораторная работа 6.1.
Имеются две выборки показателя невербального интеллекта у студентов:
| Студенты - физики | Студенты - психологи |
Задание 1. Используя «Мастер функций» вычислить основные статистические параметры (среднее значение, моду, медиану, выборочную дисперсию, размах).
Задание 2. Проверить полученные результаты, используя функцию «Описательная статистика».
Алгоритм действий:
1. В меню «Данные» открываем «Анализ» и «Анализ данных».
2. Если в меню отсутствует вкладка «Анализ», «Анализ данных», установить ее, следуя инструкциям:
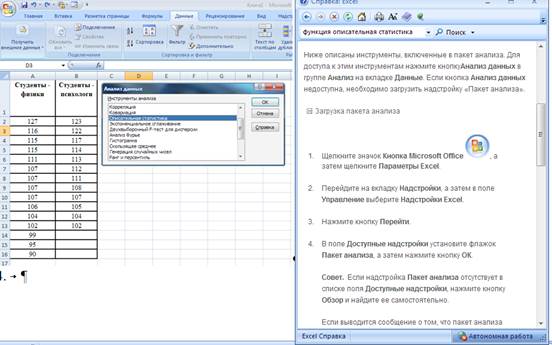
3. В этом меню выбираем «Описательная статистика». 
4. Ставим флажки «Метки в первой строке» и «Итоговая статистика», а также в окошке «Входной интервал» выделяем клетки таблицы, содержащие наши данные:

5. После выбора всех параметров на новом листе будут выведены все результаты, предусмотренные функцией «Описательная статистика»:

Опираясь на полученные данные в ыскажите предположение (гипотезу) о существовании (Н1)/ не существовании (Н0) отличий между выборками (различий в уровне невербального интеллекта у студентов-физиков и студентов-психологов).
Задание 3. Вычислить для наших двух выбороккритерии t-Стьюдента и F-Фишера.
Алгоритм действий:
1. Занесем данные, необходимые для вычисления критериев t-Стьюдента и F-Фишера в таблицу:
| Выборка | Среднее  стандартная ошибка стандартная ошибка

| Стандартное отклонение, Sx | Дисперсия выборки, S2x |
| Студенты - физики | |||
| Студенты - психологи |
2. Вычислим критерии t-Стьюдента и F-Фишера, используя формулы:

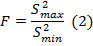
Максимальное и минимальное значение в формуле (2) выбирать с помощью функции «Если»
Задание 4. Проверим полученные результаты для критерия F-Фишера.
Алгоритм действий:
1. В меню «Данные» открываем «Анализ» и «Анализ данных».
2. Находим «Двухвыборочный F-тест для дисперсий»

3. Указываем местонахождение первого и второго массива данных, ставим флажок «Метки» и нажимаем «OK».

4. На новом листе пакета Excel получаем результаты:

Задание 5. Сделаем выводы из проведенных вычислений для критерия F-Фишера.
Из этой таблицы видно, что р – вычисленный уровень значимости, при котором нулевая гипотеза может быть отвергнута, равен 0,16:

Это значит, что различия значимы при 16 % - ном уровне. В психолого-педагогических исследованиях принят 5% уровень значимости. Делаем вывод, что различия между выборками при сравнении дисперсий по F-критерию Фишера не достоверны.
Задание 6. Проверим полученные результаты для критерия t-Стьюдента.
Алгоритм действий:
1. В меню «Данные» открываем «Анализ» и «Анализ данных».
2. Для сравнения выборок по критерию t-Стьюдента выбираем «Двухвыборочный t-тест с различными дисперсиями»:

3. Указываем местонахождение первого и второго массива данных, отмечаем «Метки». В поле «Гипотетическая средняя разность» нужно указать предполагаемую нулевой гипотезой разность средних. Пусть предполагаемая нулевой гипотезой разность средних равна 1.

4. На новом листе пакета Excel получаем результаты:

Задание 7. Сделаем выводы из проведенных вычислений для критерия t-Стьюдента.
Из таблицы видно, что p двухстороннее, т.е. вычисленный уровень значимости, при котором нулевая гипотеза может быть отвергнута, равен 0,095. Это значит, что различия значимы при 9,5 % - ном уровне. В психолого-педагогических исследованиях принят 5% уровень значимости. Делаем вывод, что различия между выборками при сравнении дисперсий по критерию t-Стьюдента также не достоверны.
Задание 8. Построить по данным выборок точечную диаграмму.