Задание множеств.
Множество обычно обозначается заглавными буквами латинского алфавита. Например, A или B. Элементы множества обозначаются маленькими буквами латинского или греческого алфавита. Например, a,b,  и т.д.
и т.д.
Запись A={a,b,c…} означает, что множество состоитиз элементов a, b, c и т.д., заданных тем или иным способом.
§ Конечное множество обычно задается перечислением всех его элементов.
Примеры задания конечных множеств:
1. Множество A путей, идущих из пункта О в пункты, М, N и К состоит из элементов a, b, c так, что
A={a,b,c};
2. Множество углов треугольника
A={30,60,90};
3. Множество букв алфавита
А={a,b,c,…,y,z};
4. Множество дней в году
A={1,2,3…,365};
5. Множество отметок за экзамен
A={2,3,4,5};
6. Множество однозначных чисел
A={1,2,3,…,9};
7. Множество решений уравнения x2-5x+6=0
A={2,3};
8. Множество знаков сравнения
A={  };
};
9. …
10. …
§ Одна из основных форм задания множества – это указание общего свойства объектов, из которых состоит множество.
A={x:P(x)}
Читается «множество всех x таких, что Р(х)...», где Р – свойство, характеризующее элементы данного множества.
Примеры: ///
Такой способ задания множества в системе аксиом ZF носит название аксиомы абстракции.
§ Множество можно задать при помощи предикатов.
Предикат – это математическое соотношение P(x), зависящее от некоторой переменной x, которое превращается в высказывание при подстановке вместе x конкретного значения.
§ При задании множества не важен порядок расположения элементов. Например, множества {a,b,c} и {a,c,b} совпадают, потому что они состоят из одинаковых элементов.
Операции над множествами.
§  Объединением множеств Aи Bназывают множество A
Объединением множеств Aи Bназывают множество A  B, которое состоит из всех элементов множеств Aи B.
B, которое состоит из всех элементов множеств Aи B.

(Объединением двух множеств называют новое множество таких элементов x, которые принадлежат или множеству A, или множеству B, или обоим множествам сразу.)
§  Пересечением множеств A и B называют множество A
Пересечением множеств A и B называют множество A  B, которое состоит из элементов, которые являются общими для A и B.
B, которое состоит из элементов, которые являются общими для A и B.

§ 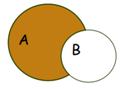 Разностью множеств Aи B называют множество A
Разностью множеств Aи B называют множество A  B, которое состоит из всех тех элементов A, которые не принадлежат B.
B, которое состоит из всех тех элементов A, которые не принадлежат B.

§ Симметрической разностью множеств A и B называют множество A  B, которое состоит из всех элементов множеств A и B, не попадающих в их пересечение.
B, которое состоит из всех элементов множеств A и B, не попадающих в их пересечение.

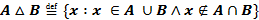
§ Декартовым (прямым) произведением множеств A и B называют множество A 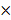 B, состоящее из упорядоченных пар (x,y), первые члены которых принадлежат множеству A, а вторые члены – множеству B. Если A=B=X, то A
B, состоящее из упорядоченных пар (x,y), первые члены которых принадлежат множеству A, а вторые члены – множеству B. Если A=B=X, то A 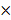 B обозначают X2.
B обозначают X2.

Например, декартовым произведением двух прямых будет плоскость, а окружности и прямой – цилиндр.
Метод математической индукции.
Метод математической индукции применяется для того, чтобы доказать истинность какого-либо математического высказывания: равенства или неравенства выражений.
Этот метод основан на принципе математической индукции (аксиоме индукции), который можно сформулировать следующим образом.
Предположение p(n) считается истинным для всех натуральных значений переменной, если выполняются следующие условия:
1. Предположение p(n) истинно для n=1.
2. Из предположения, что p(n)истинно для n=k (где k-натуральное число), следует, что оно истинно и для следующего значения n=k+1.
Под методом математической индукции понимают следующий способ доказательства. Если требуется доказать истинность предложения p(n) для всех натуральных n, то сначала проверяют истинность высказывания p(1) и заметим, допустив истинность высказывания p(k), доказывают истинность высказывания p(k+1). Если доказательство верно для каждого натурального k, то в соответствии с принципом математической индукции предложение p(n) является истинным для всех значений n.
Примеры:
1. Доказать равенство  .
.
Это равенство представляет собой предложение p(n), заданное на множестве натуральных чисел. Докажем истинность p(n) для всех значений n методом математической индукции.
I. Высказывание p(1) истинно, так как 
II. Предположим, что p(k) истинное, т.е. справедливо равенство

III. Прибавим к обеим частям равенства (k+1)2, получим

Преобразуем правую часть равенства следующим образом:

Следовательно,
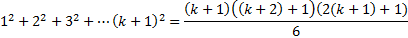
Это значит, что p(k+1) истинно. Таким образом рассуждение верно при любом  . В силу принципа математической индукции исходное равенство верно.
. В силу принципа математической индукции исходное равенство верно.
2. Доказать неравенство Бернулли. 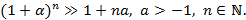
I. При n=1 получаем истинное высказывание. 
II. Предположим, что неравенство верно при n=k, т.е. 
III. Умножив обе части неравенства на 1+a (это можно сделать, т.к. a >–1), получим 
Учитывая, что  приходим к неравенству
приходим к неравенству

Итак, предположив, что данное неравенство верно для n=k, мы доказали, что оно верно и для n=k+1. Доказательство, очевидно, справедливо для каждого значения k. Неравенство доказано.
3. Доказать, что при каждом  число
число  кратно 19.
кратно 19.
I. При n=1 данное утверждение верно. 19  19.
19.
II. Предположим, что оно верно для n=k, т.е. предположим, что 
III. Тогда, так как  , то утверждение верно и при n=k+1. Действительно, первое слагаемое правой части этого равенства делится на 19 в силу индуктивного положения; второе также делится на 19, так как содержит множитель 19.
, то утверждение верно и при n=k+1. Действительно, первое слагаемое правой части этого равенства делится на 19 в силу индуктивного положения; второе также делится на 19, так как содержит множитель 19.
Оба условия принципа математической индукции выполнены. Утверждение доказано.
4. Доказать неравенство. 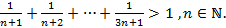
I. При n=1 неравенство справедливо, так как
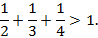
II. Предположим, что неравенство верно для n=k, т.е.
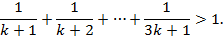
Прибавим к обеим частям неравенства сумму трёх дробей  и перенесём первое слагаемое левой части в правую часть неравенства. Тогда получим
и перенесём первое слагаемое левой части в правую часть неравенства. Тогда получим

Первая часть неравенства больше единицы, так как
 =
= 
Следовательно, левая часть тем более больше единицы, т.е.

Последнее неравенство из исходного неравенства получается при n=k+1.
Итак, предположив истинность неравенства при n=k, мы доказали его истинность при n=k+1. Таким образом, методом математической индукции неравенство доказано.
5. Пусть x1, x2,…, xn – произвольные положительные числа, причем x1x2…xn=1. Доказать, что x1+x2+…xn 
I. Если n=1, то по условию x1=1 и, следовательно, можно написать x1  1, т.е. для n=1 утверждение верно.
1, т.е. для n=1 утверждение верно.
II. Предположим, что утверждение верно для n=k. Пусть x1,x2,…,xk,xk+1 – произвольные положительные числа и x1x2…xkxk+1=1.
Могут представиться два случая: либо все эти числа равны 1, тогда их сумма равна k+1 и неравенство доказано, либо среди этих чисел есть хотя бы одно число, не равное единице, и тогда обязательно есть по крайне мере ещё одно число, не равное единице, причем, если одно из них меньше единицы, то другое больше единицы. Не ограничивая общности, можно считать, что xk>1, а xk+1<1. Рассмотрим теперь k чисел
x1,x2,…,xk-1,(xkxk+1).
Произведение их равно единице, и, следовательно, по индуктивному предположению
x1+x2+…+xk-1+xkxk+1  k.
k.
Прибавим к обеим частям последнего неравенства xk+xk+1, перенесём xkxk+1 направо и преобразуем правую часть неравенства:
x1+x2+…+xk+1  k-xkxk+1 + xk+xk+1=k+1+xk(1-xk+1)+xk+1-1= k+1+xk(1-xk+1)-(1-xk+1)=k+1+(1-xk+1)(xk-1)
k-xkxk+1 + xk+xk+1=k+1+xk(1-xk+1)+xk+1-1= k+1+xk(1-xk+1)-(1-xk+1)=k+1+(1-xk+1)(xk-1)  k+1.
k+1.
Таким образом, из истинности утверждения n=k вытекает его истинность при n=k+1. Утверждение доказано. Из приведенного доказательства следует, что знак равенства в доказываемом соотношении имеет место тогда и только тогда, когда x1=x2=…=xn=1