Текущая сумма единицы (реверсии) – это величина, обратная накопленной сумме единицы. Это текущая стоимость одной ден ед, которая должна быть получена в будущем.
Поскольку целью осуществления инвестиций является получение доходов в будущем, умножение фактора тек стоимости единицы (реверсии) на величину ожидаемого будущего дохода является основой при оценке инвестиций.
При применении фактора тек стоимости используются понятия дисконтирование и ставка дисконта, противоположные понятиям накопление и ставка процента.
На основе формулы наращения получим:
P = F/(1+r)n = F* (1+r)-n=F*FM2(r;n)
Где F – доход, планируемый к получению через n лет;
Р – текущая (приведенная, современная, сегодняшняя) стоимость, т.е. оценка величины F с позиции текущего момента;
r- %-ная ставка.
(1+r)-n называется дисконтным множителем;
1/(1+r)n – коэффициент дисконтирования.
| Пример 1.12. Сумма 5 млн руб выплачивается через 5 лет. Необходимо определить ее современную стоимость при условии, что применяется ставка сложных % = 12% годовых. Дисконтный множитель составит 1,12-5 = 0,565743, т.е. сумма уменьшается (дисконтируется) на 44%. Современная ее величина равна: P = 5 000 000 * 1,12-5 = 2 837 134,28 руб |
- Взнос на амортизацию единицы – 1/FM4
Взнос на амортизацию денежной единицы – это регулярный периодический платеж в погашение приносящего процент кредита. Он определяется как величина, обратная текущей стоимости аннуитета.
= 
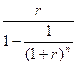
Обратную величину множителя FM 4 называют фактором обычной амортизации, или 6-й функцией сложного %.
Амортизация денежной единицы – это процесс погашения долга в течение определенного времени. Взнос на амортизацию кредита математически определяется как отношение одного платежа к первоначальной сумме кредита.
|
|
Математически взнос на амортизацию кредита определяется как отношение одного платежа к первоначальной основной сумме кредита. Взнос на амортизацию единицы показывает, каким будет обязательный периодический платеж по кредиту, включающий % и выплату основной части суммы и позволяющий погасить кредит в течение установленного срока.
Пример. В банке получена ссуда 20 000 долл на 5 лет под 13% годовых, начисляемых по схеме сложных процентов на непогашенный остаток. Возвращать нужно равными суммами в конце каждого года. Требуется определить величину годового платежа.
В этом случае текущая стоимость аннуитета – это величина депозита с общей суммой причитающихся процентов, ежегодно уменьшающаяся на равные суммы. Эта сумма годового платежа включает в себя начисленные за очередной период проценты, а также некоторую часть основной суммы долга. Таким образом, погашение суммы долга осуществляется постепенно в течение срока действия аннуитета. Структура годового платежа меняется: в начальные периоды в ней преобладают начисленные за очередной период проценты; с течением времени доля процентных платежей постоянно уменьшается и повышается доля погашаемой части основного долга.
Из предыдущих пояснений понятно, что мы имеем дело с аннуитетом постнумерандо, о котором известна его тек стоимость, % ставка и продолжительность действия. Тогда можно воспользоваться формулой:
20 000 = R*FM4(r;n), 20 000 = R*3,5172; R = 5 686 долл
или, используя формулу для амортизации кредита: 1/3,5172 = 0,2843, 0,2843*20 000 = 5686 долл
Динамика платежей
|
.
|
|
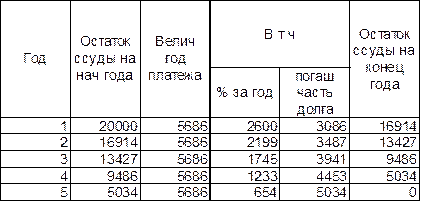
чем выше процентная ставка и/или короче срок амортизации кредита, тем выше должен быть обязательный периодический платеж. Многие кредиты предусматривают ежемесячные, поквартальные или полугодовые платежи. Для того, чтобы учесть это, необходимо разделить номинальную годовую ставку на частоту накопления и умножить число периодов в году на число лет.