Бессрочный аннуитет
Аннуитет (рента) называется бессрочной, если денежные поступления продолжаются достаточно длительное время. Математически это означает, что 
Характерным примером бессрочного аннуитета являются консоли – выпускаемые правительствами некоторых стран облигации, по которым производятся регулярные купонные выплаты, но которые не имеют фиксированного срока. В западной практике к бессрочным аннуитетам относятся аннуитеты, рассчитанные на 50 и более лет. Бессрочный аннуитет называется также вечной рентой.
В этом случае прямая задача (определение будущей стоимости) лишена смысла, однако обратная задача – определение приведенной стоимости – имеет решение.
Современная величина вечной ренты определяется просто. Математически при 
 , тогда
, тогда  (1.40)
(1.40)
Таким образом, современная стоимость вечной ренты зависит только от размера члена ренты и % ставки. Из формулы (1.40) следует, что:
 (1.41),
(1.41),
т.е. член вечной ренты = % от ее капитализированной стоимости.
Под рентой пренумерандо понимается рента с платежами в начале периодов. Различие между рентами пренумерандо и постнумерандо заключается в числе периодов начисления %. Легко понять, что каждый член последней из указанных рента «работает» на один период больше, чем в ренте постнумерандо. Отсюда наращенная сумма ренты пренумерандо, обозначим ее как  , больше в (1+r) раз аналогичной ренты постнумерандо.
, больше в (1+r) раз аналогичной ренты постнумерандо.
 (1.25);
(1.25); 
Точно такая же зависимость наблюдается и между современными стоимостями рент постнумерандо и пренумерандо.
 (1.29);
(1.29);  (1.30). Ясно, что
(1.30). Ясно, что  .
.
Важным частным случаем является рента с платежами в середине периодов. Например, в случаях, когда поступления от производственных инвестиций распределяются более или менее равномерно, применение рент пренумерандо или постнумерандо может привести к некоторым смещениям в значении получаемых показателей. Тогда для уменьшения погрешности рекомендуется суммы поступлений относить к середине периодов. Наращенные суммы и современные стоимости таких рент находим умножением обобщающих характеристик рент постнумерандо на множитель наращения за половину периода. Так, для современных стоимостей находим:
P=1; m=1;  (1.34); р=1; m>1
(1.34); р=1; m>1  (1.35);
(1.35);
p>1; m=1;  (1.36); p>1; m>1
(1.36); p>1; m>1  (1.37)
(1.37)
Отложенные ренты. Начало выплат у отложенной (отсроченной) ренты сдвинуто вперед относительно некоторого момента времени (т.е. 1-й из потока платежей начинает поступать спустя h периодов). Очевидно, что сдвиг во времени никак не отражается на величине наращенной суммы. Иное дело современная стоимость ренты. Пусть рента выплачивается спустя h периодов после некоторого начального момента времени.
Современная стоимость ренты на начало выплат (современная стоимость немедленной ренты) равна  . Современная стоимость на начало периода отсрочки, равного h лет = дисконтированной величине современной стоимости немедленной ренты. Для годовой ренты:
. Современная стоимость на начало периода отсрочки, равного h лет = дисконтированной величине современной стоимости немедленной ренты. Для годовой ренты:
 (1.38)
(1.38)
Пример. Рента постнумерандо характеризуется след параметрами: R=4 млн руб, n=5. При дисконтировании по сложной ставке %, равной 18,5% годовых, получим:
 млн руб
Таким образом, все будущие платежи оцениваются в наст момент в сумме 12,368 млн руб. Иначе говоря, 12,368 млн руб, размещенных под 18,5% годовых, обеспечивают ежегодную выплату по 4 млн руб в течение 5 лет.
Теперь предположим, что рента выплачивается не сразу, а спустя 1,5 года после момента оценки. Современная стоимость отложенной ренты составит в этом случае: млн руб
Таким образом, все будущие платежи оцениваются в наст момент в сумме 12,368 млн руб. Иначе говоря, 12,368 млн руб, размещенных под 18,5% годовых, обеспечивают ежегодную выплату по 4 млн руб в течение 5 лет.
Теперь предположим, что рента выплачивается не сразу, а спустя 1,5 года после момента оценки. Современная стоимость отложенной ренты составит в этом случае:
 млн руб млн руб
|
Если же h, т.е. число периодов отсрочки, целое число, тогда возможен вариант:
 (1.39)
(1.39)
т.е. приведенная стоимость отсроченного аннуитета представляет собой разность приведенных стоимостей аннуитетов с платежами, начиная с 1-го периода. При h=0 аннуитет становится немедленным.
Пример с изменяющейся величиной ар платы (для отложенного аннуит).
Сдан участок в аренду на 10 лет. Ар плата будет осуществляться ежегодно по схеме постнумерандо на следующих условиях: в первые 6 лет по 10 тыс руб., в оставшиеся четыре года по 11 тыс руб. требуется оценить приведенную стоимость этого договора, если % ставка, используемая аналитиком, равна 15%.

Решить данную задачу можно несколькими путями в зависимости от того, какие аннуитеты будут выделены аналитиком. Общая схема потока представлена выше. Естественно, приведенная стоимость денежного потока должна оцениваться с позиции начала 1-го временного интервала.
А) исходный поток можно представить как сумму 2-х рент: первый имеет R=10 и продолжается 10 лет; второй (отсроченный на 6 лет) имеет R=1 и продолжается 6 лет. По форм м оценить приведенную стоимость каждого аннуитета. Однако 2-й аннуитет в этом случае будет оценен с позиций 7-го года, поэтому получ сумму необх дисконтировать к началу 1-го года. В этом случае оценки 2-х рент будут приведены к одному моменту времени, а их сумма даст оценку приведенной стоимости исходного ден потока:
 =10*FM4(15%;10)+1*FM4(15%;4)*FM2 (15%;6) = 10*5,0188+1*2,8550*0,4323 = 51,422 тыс р.
=10*FM4(15%;10)+1*FM4(15%;4)*FM2 (15%;6) = 10*5,0188+1*2,8550*0,4323 = 51,422 тыс р.
Б) исходный поток можно представить как разность 2-х рент: первая имеет R=11 и продолжается 10 лет; второй имеет R=1 и, начавшись в 1-м году, заканчивается в 6-м. в этом случае расчет выглядит так:
 = 11*FM4(15%;10)-1*FM4(15%;6) = 11*5,0188-1*3,7845 = 51,422 тыс руб.
= 11*FM4(15%;10)-1*FM4(15%;6) = 11*5,0188-1*3,7845 = 51,422 тыс руб.
Наращение аннуитетов


 F?
F?
 |
 R=const
R=const
 |
Ежегодный N срочный
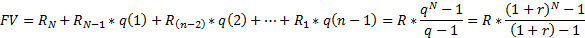

Р-срочный аннуитет (р-количество выплат в году)
F-?

 q=
q= 
(R/p руб/год) руб/р раз
 | |||||||
 | |||||||
 | |||||||
 | |||||||
 F=
F= 
1 2 ………. N*p
Платежи
Срок 1/р 2/р N
Вывод аннуитета при сроке капитализации > года, например, =  .
.
Наращение аннуитетов
| Частоты | Наращение аннуитета FV=R*Q= БС(будущая стоимость - функция Excel) БС=(ставка; кпер; плт; пс) | ||||
| Выплат | капитализации | ||||
| P | m | ||||
 БС=(r %/год; n лет; -R;……)
БС=(r %/год; n лет; -R;……)
| |||||
| m | 
‘эффективная ставка (знаменатель) БС=( Платеж в конце каждого года, а %-ты – m раз в год по ставке r
| ||||
| р |
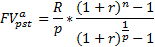 БС=(
БС=(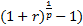 ; n*p;-R/p)) ; n*p;-R/p))
| ||||
| P | m | 
эффектиная ставка за период (знаменатель)
БС=((
| |||
| P=m | P=m |

| |||
| p≠m | p≠m |

| |||
| p-срочная | С непрерывным начислением |

| |||
Р>года, период начисления = 
|
 БС = R*
БС = R* 
| ||||
Дисконтирование аннуитетов

| Частоты | Дисконтирование аннуитета РV=R*Q= ПС(приведенная стоимость - функция Excel) ПС=(ставка; кпер; плт; пс) | |||||||||||
| Выплат | капитализации | |||||||||||
| P | m | |||||||||||

  FV
FV 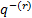 ПС=(r %/год; n лет; -R;……)
ПС=(r %/год; n лет; -R;……)
| ||||||||||||
| m | 
FV ‘эффективная ставка (знаменатель) ПС=( Платеж в конце каждого года, а %-ты – m раз в год по ставке r
| |||||||||||
| р |
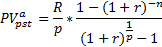 ПС=(
ПС=(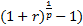 ; n*p;-R/p)) ; n*p;-R/p))
| |||||||||||
| P | m | 
эффектиная ставка за период (знаменатель)
ПС=((
| ||||||||||
| P=m | P=m |

| ||||||||||
| p≠m | p≠m |

| ||||||||||
| p-срочная | С непрерывным начислением |

| ||||||||||

 ; n;-R;……)
; n;-R;……)
 ; n*p; -(r/p))
; n*p; -(r/p))

