Табличные значения производных основных функций

Тема 4.2. Дифференциальное исчисление функции

Одной переменной

Понятие производной функции

 

Рассмотрим функцию у = f (x) при х принадлежащему некоторому отрезку [ a; b ]. Возьмем произвольную точку х₀ из этого отрезка. Для любого значения аргумента х разность х-х₀ называется приращением аргумента х в точке х₀ и обозначается Δх.

Таким образом, Δх = х – х₀.

 

Разность f (x) – f (x₀) называется приращением функции в точке х₀ и обозначается Δf (x₀).

Производной функции f(x) в точке х₀ называется предел отношения приращения функции Δf (x₀) к приращению аргумента Δх при Δх → 0 (если этот предел существует).

 

Таким образом, = =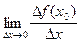

 

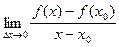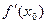
Если этот предел конечный, то функция называется дифференцируемой в точке x_o.

Производная обозначается: y ′ или f′(x) или .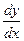

Геометрический и физический смысл производной

Пусть f(x) определена на некотором промежутке (a, b). Тогда 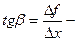тангенс угла наклона секущей МР к графику функции.

 

,

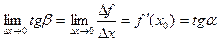где a - угол наклона касательной к графику функции f(x) в точке (x ₀, f (x ₀)).

 

Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

Уравнение касательной к кривой: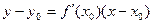

Уравнение нормали к кривой: .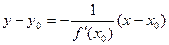

 

у

f(x)

 

 

f(x₀ +Dx) P

Df

f(x₀) M

 

a b Dx

0 x₀ x₀ + Dx x

 

 

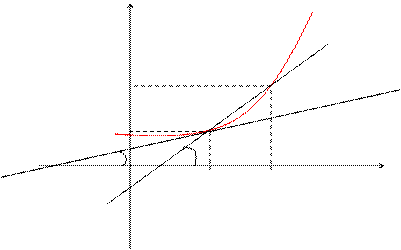
Геометрический смысл производной заключается в следующем: производная функции равна угловому коэффициенту касательной, проведенной к графику функции f (x) в точке с абсциссой x_0.

Фактически производная функции показывает скорость изменения функции, как изменяется функция при изменении переменной.

Физический смысл производной: мгновенная скорость прямолинейного движения есть первая производная от пути по времени.

Соответственно, вторая производная функции - скорость изменения скорости, т.е. ускорение.

Производная сложной функции

 

Пусть y = f(u) где u = g(x), причем область значений функции u входит в область определения функции f, т.е. задана сложная функция.

Если функция y = f(u) дифференцируема по u, а функция u = g(x) дифференцируема по х, то производная сложной функции по независимой переменной х определяется равенством:

 

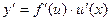
Пусть с - постоянное число, u = u (x), v = v (x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с)' = 0, (cu)' = cu ';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/ v ^2;

5) если y = f (u), u = j (x), т.е. y = f(j(x)) - сложная функция, составленная из дифференцируемых функций j и f, то у′_х = у′_u∙ u′_x.

Табличные значения производных основных функций

1. (uⁿ)' = n × u^n-1 × u' (n Î R)

2. (a^u)' = a^u × lna× u'

3. (e^u)' = e^u × u'

4.(log _a u)' = 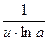× u'

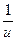5. (ln u)' = × u '

6. (sin u)' = cos u × u'

7. (cos u)' = - sin u× u'

8. (tg 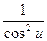u)' = × u'

9. (ctg 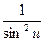u)' = - × u'

10. (arcsin 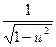u)' = × u'

11. (arccos 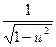u)' = - × u'

12. (arctg 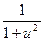u)' = × u'

13. (arcctg 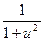u)' = - × u'

Пример. Найти производную функции у = х ⁴ + 2 х ² – 1

Для вычисления данной производной воспользуемся 1 табличным значением:

у ′ = 4 х ^4-1 + 2∙2 х = 4 х ³ +4 х

Пример. Найти производную функции у = 12 х ∙ (х ² – 8)

Для вычисления производной воспользуемся сначала 3 правилом дифференцирования (u = 12 x, v = х ² – 8), затем 1 табличным значением:

у′ = (12 х)′ ∙ (х ² – 8) + 12 х ∙ (х ² – 8)′ = 12 ∙ (х - 8) + 12 х ∙2 х = 12 х – 96 + 24 х ²

Пример. Найти производную функции у = е ^{3-4 х}

Данная функция является сложной, ее производная находится по 5 правилу дифференцирования. Обозначим u = 3 - 4 х, тогда у = е^u. Далее воспользовавшись 3 табличным значением производной, получим:

у ′ = (e^u)' = e^u × u' = е ^{3-4 х} ∙ (3 - 4 х)′ = е ^{3-4 х} ∙ (-4) = - 4 е ^{3-4 х}

Пример. Вычислить производную функции: у =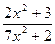

Данная производная вычисляется по 4 правилу дифференцирования (u =2 x ²+3, v =7 x ²+2):

у′ = = =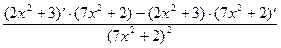

= = -

 

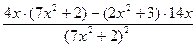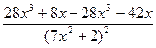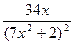
Пример. Вычислить производную функции: у = (5 х ²+3 х -7)⁶

Данная функция является сложной. Обозначим u = 5 х ²+3 х -7, получим функцию у = u⁶, для нахождения производной которой воспользуемся 1 табличным значением:

у ′ = 6 u ⁵ = 6∙(5 х ²+3 х -7)⁵ ∙ (5 х ²+3 х -7)′ = 6∙(5 х ²+3 х -7)⁵ ∙ (10 x +3)

Пример. Вычислить производную функции: у =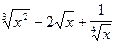

Для нахождения данной производной сначала преобразуем заданную функцию: у = 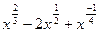. Далее воспользуемся 1 табличным значением:

у ′ = 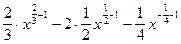= =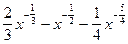