Игры с природой
Любую хозяйственную деятельность человека можно рассматривать как игру с природой. В широком смысле под "природой" понимается совокупность неопределенных факторов; влияющих на эффективность принимаемых решений. Это могут быть действительные природные физические (климатические), биологические, химические, социальные и т.п. процессы, которые сопровождают экономическую деятельность. Под "природой" может также пониматься рынок, противостоящий предпринимателю, конкурирующая среда, монополия и т.п. Безразличие природы к игре (выигрышу) дает возможность получения лицом, принимающим решение (игроком), дополнительной информации о ее состоянии. Это отличает игру с природой от обычной игры, в которой принимают участие два сознательных игрока.
Предположим, что игрок выбирает одно из m возможных управленческих решений. Ситуация, в которой он действует, является неопределенной. Известно лишь, что возможен один из n вариантов развития событий. Если будет принято i -e решение, при этом события будут развиваться по j-му варианту, то фирма, получит доход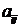 
. Матрица 
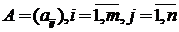называется матрицей последствий или матрицей доходов. Какое же решение следует принять игроку?
Рассмотрим две возможные ситуации: полной и частичной неопределенности.
Принятие решений в условиях полной неопределенности
Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации. В этой ситуации возможны различные стратегии игрока, отличающиеся друг от друга склонностью игрока к риску. Рассмотрим основные из них.
Правило максимакса (правило "розового оптимизма"). В этом случае игрок надеется на самый благоприятный вариант развития событий при любом выборе управленческого решения (стратегии). Поэтому для каждой стратегии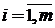 
игрок определяет максимально возможный доход, т.е. находит максимальный элемент в каждой строке матрицы А: 
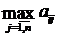. После этого игрок выбирает стратегию (строку), дающую максимально возможный максимальный доход. Таким образом, выбирается стратегия 
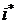, такая, что
|
|
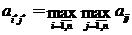. (1)
При благоприятном развитии событий, на которые рассчитывает игрок, его доход составит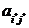 
. Однако, доход может оказаться гораздо меньше, если события будут развиваться не по оптимистичному сценарию.
Пример. Пусть матрица последствий есть
.
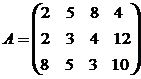Тогда при выборе 1-й стратегии максимально возможный доход составит 8 ден.ед., при выборе 2-й стратегии – 12 ден.ед., при выборе 3-й стратегии – 10 ден.ед.. По правилу максимакса игрок выбирает 2-ю стратегию. При благоприятном стечении обстоятельств (4-й вариант развития событий) игрок получит доход равный 12 ден.ед. Однако, при иных вариантах доход будет меньше. Например, при 1-м варианте развития событий доход составит всего 2 ден.ед..
Правило Вальда (правило крайнего пессимизма). В этом случае игрок настроен пессимистично и рассчитывает только на самый плохой вариант развития событий, т.е. вариант, приносящий минимальный доход. Поэтому для каждого варианта управленческого решения 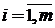игрок определяет минимально возможный доход, иными словами находит минимальный элемент в каждой строке матрицы А: 
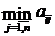. После этого игрок выбирает стратегию (строку), максимизирующую минимально возможный доход. Таким образом, выбирается стратегия 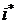, такая, что
|
|
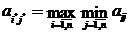. (2)
При данной стратегии игрок при любом развитии событий получит доход, не меньший, чем .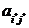
В приведенном выше примере минимально возможный доход при выборе 1-й и 2-й стратегий равен 2 ден.ед., при выборе 3-й стратегии – 3 ден.ед. Максимизируя минимально возможный доход, игрок выберет 3-ю стратегию. При этом доход игрока будет не меньше 3 ден.ед. при любом варианте развитии событий.
Правило Гурвица. Является промежуточным между правилом максимакса и правилом Вальда. В этом случае взвешиваются пессимистический и оптимистический подходы к ситуации. Принимается решение 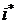, на котором достигает максимума линейная комбинация минимального и максимального дохода
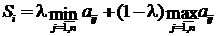, (3)
где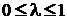 
. Значение 
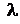называется уровнем пессимизма и выбирается из субъективных соображений. Если 
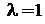, то правило Гурвица превращается в правило Вальда, а при 
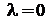, становится правилом «розового оптимизма».
Используем правило Гурвица с уровнем пессимизма 0,5 для матрицы доходов приведенного выше примера.
Для 1-й стратегии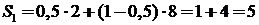 
;
для 2-й стратегии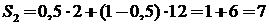 
;
для 3-й стратегии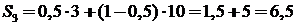 
.
Действуя по правилу Гурвица, игрок выберет 2-ю стратегию.
Правило Сэвиджа (правило минимального риска). Предположим, что произойдет j-й вариант развития событий. Если бы игрок это знал, то он получил бы доход
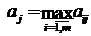. (4)
В реальности игрок не знает, какой вариант развития будет иметь место, поэтому принятая им i-я стратегия может принести меньший доход 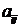. Значит принятие i-го решения несет риск недобрать
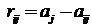. (5)
Матрица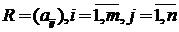 
называется матрицей рисков. Построим матрицу рисков для нашего примера. Максимально возможный доход при 1-м варианте развития событий – 8 ден.ед., поэтому элементы первого столбца матрицы рисков вычислим по формуле 
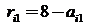. Максимально возможный доход при 2-м варианте развития событий – 5 ден.ед., поэтому элементы второго столбца матрицы рисков вычислим по формуле 
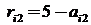. Аналогично вычислим элементы третьего и четвертого столбцов. Получим матрицу рисков
|
|
.
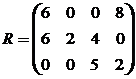При применении правила Сэвиджа анализируется матрица рисков. Для каждого варианта управленческого решения 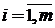игрок определяет максимально возможный риск, т.е. находит максимальный элемент в каждой строке матрицы R: 
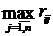. После этого игрок выбирает стратегию (строку), минимизирующую максимально возможный риск. Таким образом, выбирается стратегия 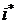, такая, что
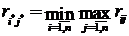. (6)
Возвращаясь к примеру, видим, что максимально возможный риск при выборе 1-й стратегии – 8 ден.ед., при выборе 2-й – 6 ден.ед, при выборе 3-й – 5 ден.ед. Минимизируя максимально возможный риск, выбираем 3-ю стратегию.
Правило Лапласа. Применяя это правило, игрок рассчитывает средний доход для каждой стратегии, предполагая, что все варианты развития событий равновероятны:
, 
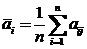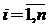. (7)
После этого игрок выбирает стратегию, максимизирующую средний доход. Таким образом, выбирается стратегия 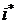, такая, что 
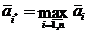. В нашем примере средний доход при выборе 1-й стратегии составит 
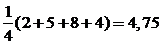ден.ед. Аналогично, вторая стратегия дает средний доход 5,25 ден.ед., третья стратегия – 6,5 ден.ед. Таким образом, действуя по правилу Лапласа, игрок выберет третью стратегию.