Предположим, что в рассматриваемой схеме известны вероятности 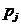 того, что реальная ситуация развивается по j-му варианту,
того, что реальная ситуация развивается по j-му варианту, 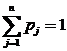 . Именно такое положение называется частичной неопределенностью. В этом случае есть несколько правил принятия решений.
. Именно такое положение называется частичной неопределенностью. В этом случае есть несколько правил принятия решений.
Правило максимальной вероятности. Согласно этому правилу игрок предполагает, что наступит наиболее вероятный исход развития событий. Для этого варианта он выбирает стратегию, дающую максимальный доход. Предположим, что в рассматриваемом примере вероятности различных вариантов заданы таблицей
| Вариант | ||||
| Вероятность | 0,2 | 0,1 | 0,3 | 0,4 |
Тогда игрок будет рассчитывать на 4-й вариант развития событий, как на наиболее вероятный, и из всех элементов 4-го столбца матрицы последствий А выберет наибольший. Соответственно, игрок предпочтет 2-ю стратегию, дающую максимальный доход 12 ден.ед.
Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации i-й стратегии, является случайной величиной 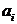 с рядом распределения
с рядом распределения
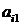
| 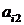
| … | 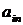
|
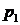
| 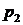
| … | 
|
Математическое ожидание
 (8)
(8)
и есть средний ожидаемый доход, обозначаемый 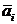 . Правило рекомендует принять решение
. Правило рекомендует принять решение 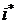 , приносящее максимальный средний ожидаемый доход
, приносящее максимальный средний ожидаемый доход 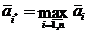 . Заметим, что в случае, когда все варианты развития событий равновероятны, правило максимизации среднего ожидаемого доходасовпадает с правилом Лапласа.
. Заметим, что в случае, когда все варианты развития событий равновероятны, правило максимизации среднего ожидаемого доходасовпадает с правилом Лапласа.
Рассчитаем средние ожидаемые доходы для рассматриваемой нами матрицы последствий А и указанных выше вероятностях:
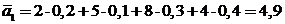 ;
;
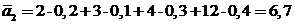 ;
;
 .
.
Максимальный средний ожидаемый доход равный 7 ден.ед., соответствует третьей стратегии.
Правило минимизации среднего ожидаемого риска. Риск фирмы при реализации i-й стратегии, является случайной величиной 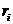 с рядом распределения
с рядом распределения
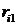
| 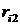
| … | 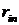
|
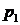
| 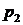
| … | 
|
Математическое ожидание
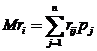 (9)
(9)
и есть средний ожидаемый риск, обозначаемый также 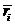 . Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.
. Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.
Вычислим средние ожидаемые риски для нашего примера при указанных выше вероятностях. Получим:
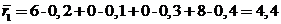 ;
;
 ;
;
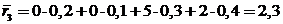 .
.
Минимальный средний ожидаемый риск равен 2,3, он соответствует третьей стратегии.
Правило, учитывающее средний ожидаемый доход и стандартное отклонение. Если принимать во внимание только ожидаемую прибыль, то наилучшей стратегией для рассматриваемого примера является 3-я стратегия. Это означает, что если бы решение о выборе стратегии принималось много раз при одних и тех же условиях, то тогда доход в среднем был бы максимально возможным и составил бы 7 ден.ед. Однако правило максимизации ожидаемого дохода не учитывает риск, связанный с выбором стратегии, т.е. «разброс» возможных вариантов развития событий. Этот риск может быть определен с помощью дисперсии и стандартного отклонения дохода. Дисперсия дохода для i-й стратегии может быть вычислена по формуле
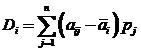 . (10)
. (10)
Стандартное отклонение представляет собой корень из дисперсии
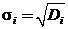 . (11)
. (11)
Проведем расчет дисперсий дохода для каждой стратегии из рассматриваемого нами примера:
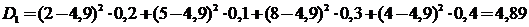 ;
;
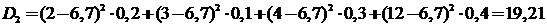 ;
;
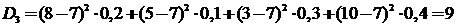 .
.
Стандартные отклонения для трех стратегий составят
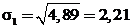 ;
; 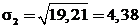 ;
; 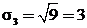 .
.
На рисунке представлены три точки, соответствующие трем стратегиям.
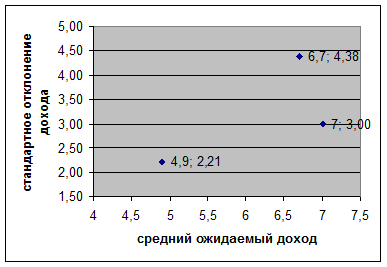
Горизонтальная координата точек – средний ожидаемый доход, вертикальная – стандартное отклонение дохода. Очевидно, что из двух стратегий игрок предпочтет ту, для которой средний ожидаемый доход больше, а риск (стандартное отклонение) меньше. Так третья стратегия предпочтительнее второй, так как имеет больший ожидаемый доход (7 ден.ед. против 6,7 ден.ед.) и меньшее стандартное отклонение (3 ден.ед. против 4,38 ден.ед.). Выбор между 1-й и 3-й стратегией не столь однозначен. С одной стороны, третья стратегия дает больший ожидаемый доход (7 ден.ед. против 4,9 ден.ед.). С другой стороны, она более рискованная, так как стандартное отклонение дохода для 3-й стратегии равно 3 ден.ед., а для 1-й стратегии – 2,21 ден.ед. Также неоднозначен выбор между 1-й и 2-й стратегией.
Понятно, что если среди всех точек на графике найдется точка, лежащая одновременно правее и ниже всех других точек, то именно эта точка и определяет наилучшую стратегию. Если таких точек нет (как в нашем примере), то среднему ожидаемому доходу и среднему ожидаемому риску присваиваются определенные веса. В результате каждое решение будет характеризоваться одной величиной, по которой и определяется наилучшая стратегия. Например, 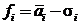 или
или 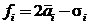 . Первая формула говорит о том, что риск и доход одинаково важны для игрока. Вторая формула предполагает, что доход ценится в два раза больше, чем риск. Выберем оптимальную стратегию для нашего примера исходя из критерия максимума
. Первая формула говорит о том, что риск и доход одинаково важны для игрока. Вторая формула предполагает, что доход ценится в два раза больше, чем риск. Выберем оптимальную стратегию для нашего примера исходя из критерия максимума 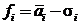 . Имеем:
. Имеем:
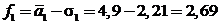 ;
;
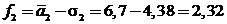 ;
;
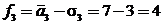 .
.
Игрок выбирает третью стратегию.
Решение типовой задачи
Задание 1. Себестоимость пирожка с яблоками, выпускаемого в кондитерской «1000 калорий», составляет 13 руб. Розничная цена свежего пирожка составляет 17 руб., а невостребованные за день пирожки передаются в организации помощи неимущим по оптовой цене 3 руб. за штуку. Сколько пирожков надо производить в день, если известно, что спрос на них составляет от 2 до 6 штук ежедневно?
1. Решите задачу при помощи методов, применяемых в условиях полной неопределенности:
- правила максимакса,
- правила Вальда,
- правила Сэвиджа,
- правила Лапласа,
- критерия Гурвица при уровне пессимизма 0,3.
2. Предположим, что известна статистика продаж за 50 дней:
| Продано пирожков в день | |||||
| Частота |
Решите задачу при помощи методов, применяемых в условиях частичной неопределенности:
- правила максимальной вероятности,
- правила максимизации ожидаемого дохода,
- правила минимизации возможных потерь;
- правила, учитывающего средний ожидаемый доход и стандартное отклонение.