| Продано пирожков в день | |||||
| Частота | |||||
| Относительная частота (вероятность) | 0,3 | 0,3 | 0,22 | 0,14 | 0,04 |
Наиболее часто продается 2 или 3 пирожка в день (вероятность 0,3 для каждого случая). Поэтому по правилу максимальной вероятности следует выпускать 2 или 3 пирожка.
9. Расчет ожидаемых прибылей для каждого объема производства по формуле 8. Оформление результата в виде таблицы. В ячейках таблицы разместим произведение прибыли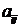 
на вероятность соответствующего спроса 
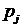, далее просуммируем элементы в каждой строке.
Таблица 6
Ожидаемые прибыли
| Объем производства | Возможные исходы: спрос пирожков в день | Ожидаемая прибыль | ||||
| 2,4 | 2,4 | 1,76 | 1,12 | 0,32 | ||
| -0,6 | 3,6 | 2,64 | 1,68 | 0,48 | 7,8 | |
| -3,6 | 0,6 | 3,52 | 2,24 | 0,64 | 3,4 | |
| -6,6 | -2,4 | 1,32 | 2,8 | 0,8 | -4,08 | |
| -9,6 | -5,4 | -0,88 | 1,4 | 0,96 | -13,52 |
Наибольший ожидаемый доход 8 рублей получается при выпуске 2 пирожков. Поэтому по правилу максимизации ожидаемого дохода следует выпускать 2 пирожка.
10. Расчет ожидаемых рисков для каждого объема производства по формуле 9. Оформление результата в виде таблицы. В ячейках таблицы разместим произведение риска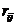 
на вероятность соответствующего спроса 
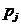, далее просуммируем элементы в каждой строке.
Таблица 7
Ожидаемые риски
| Объем производства | Возможные исходы: спрос пирожков в день | Ожидаемый риск | ||||
| 2,4 | 3,52 | 3,36 | 1,28 | 10,56 | ||
| 2,7 | 1,76 | 2,24 | 0,96 | 7,66 | ||
| 5,4 | 2,7 | 1,12 | 0,64 | 9,86 | ||
| 8,1 | 5,4 | 1,98 | 0,32 | 15,8 | ||
| 10,8 | 8,1 | 3,96 | 1,26 | 24,12 |
Наименьший ожидаемый риск 7,66 рублей получается при выпуске 3 пирожков. Поэтому по правилу минимизации ожидаемого риска следует выпускать 3 пирожка.
11. Расчет дисперсий и стандартных отклонений для каждого объема производства по формулам 10 и 11. Оформление результата в виде таблицы. В ячейках таблицы разместим произведение квадрата отклонения прибыли от ожидаемого значения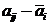 
на вероятность соответствующего спроса 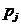, далее просуммировав элементы в каждой строке, получим дисперсии.
Таблица 8
Дисперсии и стандартные отклонения
| Объем производства | Возможные исходы: спрос пирожков в день | Дисперсия | Стандартное отклонение | ||||
| 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | 0,00 | |
| 28,81 | 5,29 | 3,88 | 2,47 | 0,71 | 41,16 | 6,42 | |
| 71,15 | 0,59 | 34,93 | 22,23 | 6,35 | 135,24 | 11,63 | |
| 96,34 | 4,61 | 22,35 | 81,18 | 23,19 | 227,67 | 15,09 | |
| 102,45 | 6,02 | 19,94 | 77,45 | 56,31 | 262,17 | 16,19 |
12. Построение точечной диаграммы.
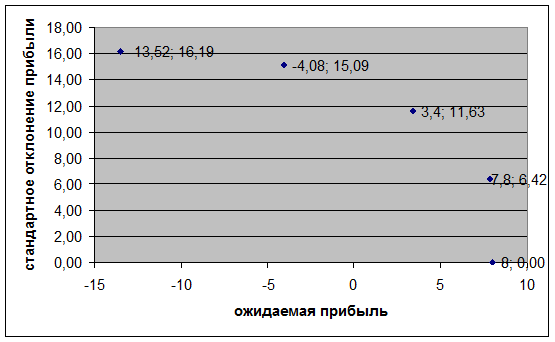
Анализ диаграммы показывает, что наилучшим решением является выбор объема производства 2 пирожка, так как при этом достигается наибольшая ожидаемая прибыль и наименьшее стандартное отклонение, т.е. наименьший риск.
Задание 2.
Себестоимость пончика, выпускаемого в супермаркете «Реал», составляет 9 руб. Розничная цена свежего пончика составляет 16 руб., а невостребованное за день сдается на свиноферму по оптовой цене 1 руб. за штуку.
Сколько пончиков надо производить в день, если известно, что спрос на них составляет от 7 до 11 штук ежедневно?
1. Решите задачу при помощи методов, применяемых в условиях полной неопределенности:
- правила максимакса,
- правила Вальда,
- правила Сэвиджа,
- правила Лапласа,
- критерия Гурвица при уровне пессимизма 0,4.
2. Предположим, что известна статистика продаж за 50 дней:
| Продано пончиков в день | |||||
| Частота |
Сколько пирожков надо производить в день?
Решите задачу при помощи методов, применяемых в условиях частичной неопределенности:
- правила максимальной вероятности,
- правила максимизации ожидаемого дохода,
- правила минимизации возможных потерь;
- правила, учитывающего средний ожидаемый доход и средний риск.
Задание 3.
Себестоимость медовика, выпускаемого кондитерским цехом «Царь-продукт», составляет 11 руб. Розничная цена свежего медовика составляет 19 руб., а невостребованное за день передается в филиал по оптовой цене 2 руб. за штуку. Сколько медовиков надо производить в день, если известно, что спрос на них составляет от 80 до 100 штук ежедневно?
1. Решите задачу при помощи методов, применяемых в условиях полной неопределенности:
- правила максимакса,
- правила Вальда,
- правила Сэвиджа,
- правила Лапласа,
- критерия Гурвица при уровне пессимизма 0,3.
2. Предположим, что известна статистика продаж за 180 дней:
| Продано в день | |||||||||||
| Частота | |||||||||||
| Продано в день | |||||||||||
| Частота |
Сколько медовиков надо производить в день?
Решите задачу при помощи методов, применяемых в условиях частичной неопределенности:
- правила максимальной вероятности,
- правила максимизации ожидаемого дохода,
- правила минимизации возможных потерь;
- правила, учитывающего средний ожидаемый доход и средний риск.
Задание 4. Сельскохозяйственное предприятие может реализовать некоторую продукцию:
А1) сразу после уборки;
А2) в зимние месяцы;
А3) в весенние месяцы.
Прибыль зависит от цены реализации в данный период времени, затратами на хранение и возможных потерь. Размер прибыли, рассчитанный для разных состояний-соотношений этих факторов (S1, S2 и S3), в течение всего периода реализации, представлен в виде матрицы (млн. руб.)
| S1 | S2 | S3 | |
| A1 | -3 | ||
| A2 | -1 | ||
| A3 | -7 | -3 |
Определить наиболее выгодную стратегию по всем критериям (максимакса, Вальда, Сэвиджа, Лапласа, Гурвица, максимального ожидаемого дохода, минимального ожидаемого риска, критерия, учитывающего средний ожидаемый доход и средний риск), если вероятности состояний: 0,2; 0,5; 0,3; коэффициент пессимизма 0,6.
Задание 5. Магазин продает скоропортящуюся продукцию по 50 рублей за ящик, закупая ее у поставщиков по 20 рублей за ящик. Непроданная в течение дня продукция реализуется в конце дня по 5 рублей за ящик. Суточный спрос на продукцию колеблется от 0 до 10 ящиков.
1) Сколько ящиков продукции должен закупать у оптовиков магазин ежедневно, если других сведений о спросе нет? Для решения применить правила максимакса, Вальда, Сэвиджа, Лапласа, Гурвица с уровнем пессимизма 0,7.
2) Сколько ящиков продукции должен закупать у оптовиков магазин ежедневно, если известны данные о продажах за последние пятьдесят дней?
| Количество проданных ящиков | |||||||||||
| Количество дней продаж |
Для решения применить правила максимизации ожидаемого дохода, минимизации ожидаемого риска и правила, учитывающего ожидаемый доход и риск.
Задание 6. Условия задачи конкретизируются по двум последним цифрам номера зачетной книжки. Предпоследняя цифра «k», последняя «m».
Себестоимость единицы продукции, выпускаемой фирмой, составляет (20+k) у.е., цена продажи – (32+m) у.е. Непроданную в течение дня продукцию можно реализовать по цене ниже себестоимости на 10 у.е.Суточный спрос на продукцию колеблется от (40+2k) до (52+2k) единиц.
1) Сколько единиц продукции должна производить фирма ежедневно, если других сведений о спросе нет? Для решения применить правила максимакса, Вальда, Сэвиджа, Лапласа, Гурвица с уровнем пессимизма m/10.
2) Сколько единиц продукции должна производить фирма ежедневно, если на основе данных предшествующего периода о величине спроса распределение спроса оценивается таблицей:
| Количество проданных изделий | 40+2k | 43+2k | 46+2k | 49+2k | 52+2k |
| Частота (вероятность) | 0.11 | 0.22 | 0.30 | 0.25 | 0.12 |