6.1. Перечень компетенций выпускников образовательной программы с указанием результатов обучения (знаний, умений, владений), характеризующих этапы их формирования, описание показателей и критериев оценивания компетенций на различных этапах их формирования.
ОПК-2. Способностью использовать в профессиональной деятельности базовые знания фундаментальных разделов математики, создавать математические модели типовых профессиональных задач и интерпретировать полученные результаты с учетом границ применимости моделей
| Планируемые результаты обучения*(показатели достижения заданного уровня освоения компетенций) | Критерии оценивания результатов обучения по семибалльной шкале | ||||||
| Плохо | Неудовлетворительно | Удовлетворительно | Хорошо | Очень хорошо | Отлично | Превосходно | |
| У1 (ОПК-2) Уметьрешать в рамках профессиональной деятельности задачи, требующие знания основ моделирования геометрических объектов | Отсутствие умений | Фрагментарное присутствие умений без положительного результата решения типовой задачи в рамках дисциплины | Успешная демонстрация умений лишь для некоторых базовых задач в рамках дисциплины | Успешная демонстрация умений для всех базовых задач в рамках дисциплины | Успешная демонстрация умений для всех базовых и некоторых дополнительных задач в рамках дисциплины | Успешная демонстрация умений для всех базовых и дополнительных задач в рамках дисциплины | Успешная демонстрация умений для всех базовых и дополнительных задач, в том числе повышенной трудности |
| З1 (ОПК-2) Знать границы применимости и возможности использования моделей геометрических объектов | Отсутствие знаний | Фрагментарные знания без положительного результата решения типовой задачи в рамках дисциплины | Успешная демонстрация знаний лишь для некоторых базовых задач в рамках дисциплины | Успешная демонстрация знаний для всех базовых задач в рамках дисциплины | Успешная демонстрация знаний для всех базовых и некоторых дополнительных задач в рамках дисциплины | Успешная демонстрация знаний для всех базовых и дополнительных тем дисциплины | Успешная демонстрация знаний для всех базовых и дополнительных тем дисциплины, в том числе повышенной трудности |
| В1 (ОПК-2) Владеть навыками, требующимися для решения задач моделирования геометрических объектов | Отсутствие навыков | Фрагментарные навыки без положительного результата решения типовой задачи в рамках дисциплины | Успешная демонстрация навыков решения задач лишь для некоторых базовых задач в рамках дисциплины | Успешная демонстрация навыков решения для всех базовых задач в рамках дисциплины | Успешная демонстрация навыков решения для всех базовых и некоторых дополнительных задач в рамках дисциплины | Успешная демонстрация навыков решения всех базовых и дополнительных задач в рамках дисциплины | Успешная демонстрация навыков решения всех базовых и дополнительных задач в рамках дисциплины, в том числе повышенной трудности |
| М1 (ОПК-2) Учебная активность и сформированность мотивации к овладению аналитической геометрии как фундаментальным разделом математики | Отсутствие положительной мотивации | Фрагментарные проявления положительной мотивации без положительного результата решения типовой задачи в рамках дисциплины | Успешная демонстрация проявления положительной мотивации лишь для некоторых базовых задач в рамках дисциплины | Успешная демонстрация проявления положительной мотивации для всех базовых задач в рамках дисциплины | Успешная демонстрация проявления положительной мотивации для всех базовых и некоторых дополнительных задач в рамках дисциплины | Успешная демонстрация проявления положительной мотивации для решения всех базовых и дополнительных задач в рамках дисциплины | Успешная демонстрация проявления положительной мотивации для решения всех базовых и дополнительных задач в рамках дисциплины, в том числе повышенной трудности |
|
|
|
|
6.2. Описание шкал оценивания.
Промежуточной аттестацией для дисциплины «Аналитическая геометрия» является устный экзамен, по итогам которого выставляется оценка по семибалльной шкале: оценки «Плохо» и «Неудовлетворительно» означают отсутствие аттестации, оценки «Удовлетворительно», «Хорошо», «Очень хорошо», «Отлично» и «Превосходно» выставляются при успешном прохождении аттестации.
6.3. Критерии и процедуры оценивания результатов обучения по дисциплине, характеризующих этапы формирования компетенций
Промежуточной аттестацией для дисциплины «Аналитическая геометрия» является устный экзамен, на котором обучаемые представляют развернутый ответ на теоретический вопрос, содержащийся в списке «Контрольные вопросы», приведённом ниже в разделе 6.4.1. настоящей программы, и решение задачи, типовые примеры для которой приведены в разделе 6.4.2. настоящей программы. Кроме того, обучающиеся отвечают на один-два дополнительных вопроса экзаменатора. Критериями для выставления оценки являются следующие индикаторы:
|
|
· Знание обучающимися основных теоретических положений дисциплины, умение представить их грамотное изложение в виде основных формул, теорем и поясняющих чертежей;
· Умение обучающихся представить вывод тех или иных теоретических положений, теорем и результатов курса;
· Навыки обучающихся в решении практических задач той или иной степени сложности.
В зависимости от успешности выполнения данных критериев на промежуточной аттестации (устном экзамене) выставляется одна из следующих оценок:
«Плохо» - обучающийся не продемонстрировал никаких знаний об основных теоретических разделах курса и не показал никаких практических навыков решения основных задач.
«Неудовлетворительно» - обучающийся не продемонстрировал представления об основных теоретических разделах курса и не показал удовлетворительных практических навыков решения основных задач.
«Удовлетворительно» - обучающийся продемонстрировал изложение только формулировок основных теоретических положений курса без их обоснования и с использованием наводящих вопросов от экзаменатора, и успешно продемонстрировал практических навыков решения лишь самых простых задач
«Хорошо» - обучающийся продемонстрировал связное изложение основных теоретических положений курса и их обоснование, и незначительными наводящими вопросами экзаменатора, и успешно продемонстрировал практические навыки решения задач, но не смог ответить на дополнительный вопрос или решить дополнительную задачу.
«Очень хорошо» - обучающийся продемонстрировал самостоятельно изложение всех теоретических положений курса и их обоснование, успешно продемонстрировал практические навыки решения задач, но не смог ответить на дополнительный вопрос или решить дополнительную задачу повышенной трудности.
«Отлично» - обучающийся продемонстрировал высокий уровень в самостоятельном изложении всех теоретических положений курса и их обосновании, успешно продемонстрировал практические навыки решения задач, и смог ответить на дополнительный вопрос или решить дополнительную задачу повышенной трудности.
«Превосходно» - обучающийся продемонстрировал выдающийся уровень знаний в самостоятельном изложении всех теоретических положений курса и их обосновании, успешно продемонстрировал практические навыки решения задач, и смог ответить на дополнительный вопрос или решить дополнительную задачу повышенной трудности.
6.4. Типовые контрольные задания или иные материалы, необходимые для оценки результатов обучения, характеризующих этапы формирования компетенций и (или) для итогового контроля сформированности компетенции.
6.4.1. При проведении промежуточной аттестации обучающимся предлагаются следующие контрольные вопросы, охватывающие программу дисциплины «Аналитическая геометрия»:
- Декартовы координаты на плоскости. Деление отрезка в заданном отношении. Уравнение кривой на плоскости.
- Полярные координаты на плоскости. Цилиндрические и сферические координаты в пространстве.
- Определители и системы линейных уравнений 2-го и 3-го порядков. Формулы Крамера.
- Понятие вектора. Линейные операции. Линейная независимость и базис.
- Переход от одного базиса к другому на плоскости и в пространстве.
- Скалярное произведение векторов. Ортонормированный базис.
- Векторное и смешанное произведение векторов.
- Условия компланарности и коллинеарности векторов.
- Уравнения первой степени: прямая линия на плоскости и плоскость в пространстве.
- Уравнения прямой линии на плоскости. Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.
- Расстояние от точки до прямой на плоскости. Основные задачи на прямую на плоскости. Пучок прямых.
- Плоскость и прямая в пространстве. Координатные и векторные уравнения.
- Параллельность плоскостей в пространстве. Прямая как линия пересечения двух плоскостей.
- Основные задачи на плоскость и прямую в пространстве. Расстояние от точки до плоскости и от точки до прямой.
- Алгебраические линии и поверхности. Цилиндры и конусы.
- Конические сечения, уравнения в полярных координатах.
- Канонические уравнения эллипса, гиперболы и параболы. Вывод из уравнений в полярных координатах.
- Эллипс, гипербола и парабола как алгебраические линии второго порядка.
- Основные свойства эллипса, гиперболы и параболы. Фокусы и директрисы.
- Касательные к эллипсу, гиперболе и параболе.
- Параметрическое уравнение эллипса. Эллипс как проекция окружности на плоскость и эллипс как сечение круглого цилиндра.
- Пересечение кривой второго порядка и прямой. Асимптотические направления.
- Поверхности второго порядка. Центр поверхности.
- Стандартное упрощение уравнения поверхности второго порядка через поворот системы координат.
- Классификация центральных поверхностей второго порядка.
- Классификация нецентральных поверхностей второго порядка.
- Прямолинейные образующие поверхностей второго порядка.
6.4.2. Примеры задач для практических занятий, самостоятельной работы студентов, а также для проведения контрольных работ, промежуточной аттестации:
1. Введение. Метод координат.
1.1.Даны точки 
и 
. Определить координаты точки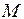 
, симметричной точке 
относительно точки 
, и координаты точки 
, симметричной точке 
относительно точки 
.
1.2.Составить уравнение геометрического места точек, равноудалённых от двух данных точек 
и 
.
1.3.Точка 
со скоростью 
равномерно движется по прямой 
, которая равномерно вращается вокруг точки 
(начала координат) с постоянной угловой скоростью 
. Траектория точки 
на плоскости 
называется спиралью Архимеда. Составить её уравнение в полярных координатах.