Определение вектора в пространстве ничем не отличается от определения вектора на плоскости.
& Определение 1. Вектором называется направленный отрезок, т.е. отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Векторы обозначаются  и т. п. и на чертеже изображаются стрелкой.
и т. п. и на чертеже изображаются стрелкой.
& Определение 2. Длиной (или модулем) вектора  называется длина отрезка
называется длина отрезка  .
.
Длина векторов  обозначается
обозначается  .
.
Любая точка пространства также считается вектором, который называется нулевым. Начало такого вектора совпадает с его концом, а длина равна нулю. Обозначения нулевого вектора: 
& Определение 3. Векторы  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если ненулевые векторы 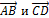 лежат на параллельных прямых (следовательно, в одной плоскости), причём лучи
лежат на параллельных прямых (следовательно, в одной плоскости), причём лучи 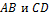 лежат в одной полуплоскости, границей которой является прямая
лежат в одной полуплоскости, границей которой является прямая  , то векторы
, то векторы 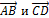 называются сонаправленными; в случае же, когда эти векторы принадлежат одной прямой, они называются сонаправленными, если один из лучей
называются сонаправленными; в случае же, когда эти векторы принадлежат одной прямой, они называются сонаправленными, если один из лучей  или
или  целиком содержится в другом.
целиком содержится в другом.
Нулевой вектор будем считать сонаправленным с любым вектором в пространстве.
Сонаправленные векторы, в силу их определения, коллинеарны. Если два коллинеарных вектора не сонаправлены, то они называются противоположно направленными.
Обозначения:  (векторы сонаправлены),
(векторы сонаправлены),  (векторы противоположно направлены).
(векторы противоположно направлены).
& Определение 4. Векторы  называются равными, если
называются равными, если 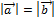 и
и  (т.е. если векторы сонаправлены и их длины равны).
(т.е. если векторы сонаправлены и их длины равны).
& Теорема 1. От любой точки пространства можно отложить вектор, равный данному, и притом только один.
Доказательство этой теоремы аналогично доказательству соответствующей планиметрической теоремы.
& Операции над векторами и их свойства.
Пусть даны два вектора  . В силу теоремы 1 от произвольной точки . В силу теоремы 1 от произвольной точки 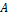 пространства можно отложить вектор пространства можно отложить вектор  , а от точки , а от точки  — вектор — вектор  , тогда вектор , тогда вектор  называется по определению суммой векторов называется по определению суммой векторов  , а описанное правило построения суммы двух векторов — правилом треугольника. , а описанное правило построения суммы двух векторов — правилом треугольника.
| 
|
& Теорема 2. Сумма  векторов
векторов  не зависит от выбора точки
не зависит от выбора точки 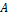 , от которой при сложении откладывается вектор
, от которой при сложении откладывается вектор  .
.
Правило треугольника можно сформулировать и так: для любых трёх точек  пространства выполняется равенство
пространства выполняется равенство 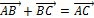 .
.
Кроме того, сумму двух неколлинеарных векторов с общим началом можно построить и по правилу параллелограмма:  , где , где  — вектор, модуль которого равен длине диагонали параллелограмма, построенного на векторах — вектор, модуль которого равен длине диагонали параллелограмма, построенного на векторах  , причём вектор , причём вектор  откладывают от той же точки, что и векторы откладывают от той же точки, что и векторы  .
Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве: .
Все свойства операции сложения векторов, справедливые на плоскости, остаются справедливыми и в пространстве:


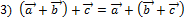 , где , где  произвольные векторы в пространстве. произвольные векторы в пространстве.
| 
|
& Определение 5. Два ненулевых вектора называются противоположными, если их длины равны и эти векторы противоположно направлены.
Вектор, противоположный данному ненулевому вектору  , обозначается , обозначается  .
& Определение 6. Разностью двух векторов .
& Определение 6. Разностью двух векторов  называется вектор называется вектор  такой, что его сумма с вектором такой, что его сумма с вектором  равна вектору равна вектору  .
Разность векторов .
Разность векторов  обозначается обозначается  . Таким образом, по определению . Таким образом, по определению  , если , если  .
Разность векторов .
Разность векторов  можно найти по формуле можно найти по формуле  .
(докажите эту формулу самостоятельно). .
(докажите эту формулу самостоятельно).
| 
| |
| Замечание. Так же как и на плоскости, для сложения нескольких векторов в пространстве можно использовать правило многоугольника, только в последнем случае этот многоугольник будет пространственным (т.е. не все векторы, его составляющие, лежат в одной плоскости). Из законов сложения векторов следует, что сумма нескольких векторов не зависит от порядка слагаемых. | 
| |
& Определение 7. Произведением ненулевого вектора  на действительное число
на действительное число  называется вектор
называется вектор  , длина которого равна произведению длины вектора
, длина которого равна произведению длины вектора  на модуль числа k,
на модуль числа k,
причём вектор  сонаправлен с вектором
сонаправлен с вектором  при k > 0 и противоположно направлен вектору
при k > 0 и противоположно направлен вектору  при
при  .
.
Таким образом, по определению,  , если
, если  , причём
, причём  при
при  и
и  при
при  . Ясно, что векторы
. Ясно, что векторы  коллинеарны. Если же
коллинеарны. Если же  или k = 0, то
или k = 0, то  и
и 
& Свойства умножения вектора на число:


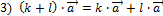 , где
, где  произвольные векторы, а
произвольные векторы, а  - произвольные числа.
- произвольные числа.
Справедлива также лемма о коллинеарных векторах: если векторы  коллинеарны и
коллинеарны и 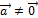 , то существует такое действительное число
, то существует такое действительное число  , что,
, что,  .
.
& Теорема 3. Пусть  , где , где  - некоторое действительное число, отличное от - некоторое действительное число, отличное от  , тогда точки , тогда точки  принадлежат одной прямой. Для произвольной точки принадлежат одной прямой. Для произвольной точки  пространства справедливо равенство: пространства справедливо равенство:

| 
|
Следствие 1. Если 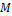 — середина отрезка — середина отрезка  , то для любой точки , то для любой точки  пространства справедливо пространства справедливо
 (в данном случае
(в данном случае  ). ).
| 
|
Следствие 2. Если точка 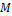 делит отрезок делит отрезок  в отношении в отношении  , т.е. , т.е.  , то для любой точки , то для любой точки  пространства пространства
 (в данном случае
(в данном случае  ). ).
| 
|
Следствие 3. Если точки  делят соответственно отрезки делят соответственно отрезки 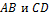 в равных отношениях, т. е. в равных отношениях, т. е.  , то , то
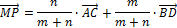 Как видим, почти все определения и утверждения, рассмотренные выше (за исключением, быть может, правила сложения нескольких векторов), аналогичны соответствующим определениям и утверждениям планиметрии.
Как видим, почти все определения и утверждения, рассмотренные выше (за исключением, быть может, правила сложения нескольких векторов), аналогичны соответствующим определениям и утверждениям планиметрии.
| 
|
1. Дано: 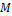 – точка пересечения медиан
– точка пересечения медиан  . Докажите, что
. Докажите, что 
2. Дано: 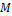 – точка пересечения медиан
– точка пересечения медиан  ,
,  – любая точка пространства. Докажите, что
– любая точка пространства. Докажите, что 
3. Повторение упр. 299.
4. Упр. 321, 322.
5. Дано:  – тетраэдр,
– тетраэдр,  точки пересечения медиан (центроиды) граней
точки пересечения медиан (центроиды) граней  соответственно. Докажите, что:
соответственно. Докажите, что: 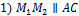 ;
;  .
.
6. Дано:  параллелепипед. На диагонали
параллелепипед. На диагонали  грани
грани  взята такая точка
взята такая точка 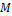 , что
, что  , на диагонали
, на диагонали  параллелепипеда – такая точка
параллелепипеда – такая точка  , что
, что  . Докажите, что:
. Докажите, что:  лежат на одной прямой; 2) найдите отношение, в котором точка
лежат на одной прямой; 2) найдите отношение, в котором точка  делит
делит  .
.
7. Даны два параллелограмма  и
и  Точки
Точки  середины соответственно
середины соответственно  . Докажите, что отрезки
. Докажите, что отрезки 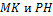 пересекаются в одной точке и делятся ею пополам.
пересекаются в одной точке и делятся ею пополам.