Сущность аналитических методов решения задачи линейного программирования позволяет истолковать ее геометрическое представление.
Заметим, что геометрическое изображение задачи можно дать одно-, двух- и трехмерных случаев.
Однако полученные выводы можно распространить на n -мерный случай.
Для построения решения задачи линейного программирования графическим методом следует четко представить себе понятие вектора - градиента как направления наискорейшего возрастания формы F.
Строим область решений системы ограничений задачи, которая представляет собой выпуклый многогранник Ω (в случае ее совместности), и, например, нулевой уровень линейной формы F (F=0).
Находим вектор градиент gradF =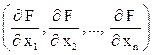 
.
Будем иметь ввиду, что оптимальные решения, если они существуют, достигаются в вершинах многогранника Ω.
При этом могут представиться следующие случаи:
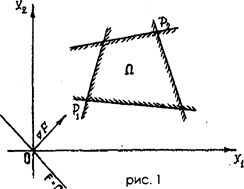min F=F(P1); max F= F(P2)
Решение задачи минимизации - координаты вершины Р1, максимизации -координаты вершины Р2.
min F=F(P2); max F= F(P1)
Решение задачи минимизации - координаты вершины Р2, максимизации -координаты вершины Р1.
рис.5
Пример:
Найти Fmах и Fmin:
F = х1 + 1.5х2,
2х1 + Зх2 
6
х1 + 4х2 4
х1 
0
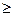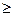х2 0
Уравнения границ многоугольника решений:
(1) 2х1 + 3х2 =6 (1) 
Прямая F=0 параллельна отрезку Р1Р2, min F достигается в каждой точке отрезка Р1Р2, уравнение которого
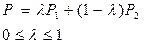
Итак, задача имеет бесчисленное множество точек минимума. Максимум достигается в точке P3.
На рис. 4 изображен случай неограниченности снизу линейной формы F на многогранникеΩ.
На рис. 5 изображен случай несовместимости системы ограниченной задачи.
(II) x1 + 4x2 =4 или (II)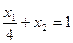 
(III) x1 = 0 (III) x1 = 0
(IV) x2 = 0 (IV) x2 = 0
Строим границы по закону соответствующего неравенства отмечаем штриховой полуплоскость - решение данного неравенства.
Далее строим нулевой уровень линейной формы F = x1 +1,5х2 =0, при этом gradF ==(1; 1,5).
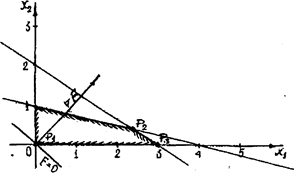
Fmin = F (P1)
P1 (0; 0)
Итак, точка минимума x1 = 0, x2 = 0.
Очевидно, (F=0)║ P2P3.
Задача имеет бесчисленное множество точек максимума.
Найдем координаты точки P2 (x'1, x'2) и P3 (x''1, x''2).
Точка Р2 лежит на пересечении прямых I и II. Решаем совместно эти уравнения.
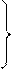2x1 + 3x2 = 6
x'1 = 2,4; x'2= 0,4
x1 +4x2 = 4
Точка P3 лежит на пересечении прямых I и IV.
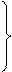2x1 + 3x2 = 6
x''1 = 3; x''2= 0
x2 = 0
F max = F(P2) = F(P3) = F(P)
где Р - произвольная точка отрезка P2P3
Fmax =xi +1,5х2 =3
Пользуясь геометрической интерпретацией задачи линейного программирования, можно сделать выводы:
1. Если оптимальное решение задачи линейного программирования существует, то оно достигается в вершине многогранника решения Ω.
2. Если оптимальное решение достигается в более чем одной вершине, то оно достигается в любой точке их выпуклой линейной комбинации.
3. Для существования оптимального решения необходимо и достаточно, чтобы многогранник решений Ω содержал хотя бы одну точку и максимизируемая линейная форма была бы ограничена сверху.
Задачи для самостоятельного решения
| х |
Следующие задачи линейного программирования решить графически (или убедиться в их неразрешимости).
| 1) | 
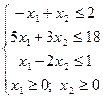
| 2) | 
| |
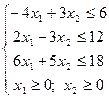
| 3) |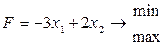 
| 4) | 
| |
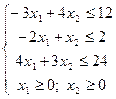
| 5) |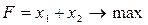 
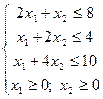
| 6) | 
| |
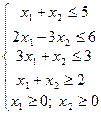
| 7) | 
| 8) |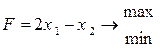 
| |
| 9) |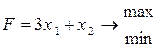 
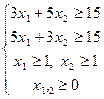
| 10) | 
| |
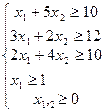
| 11) | 
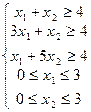
| 12) |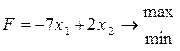 
| |
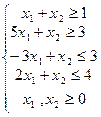
| 13) | 
| 14) |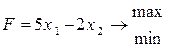 
| |
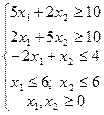
| 15) |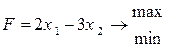 
| 16)0) | 
| |
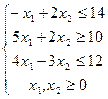
| 17)0) |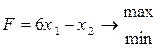 
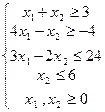
| 18) | 
| |
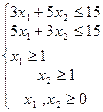
| 19) |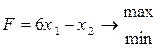
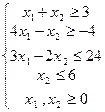
| 20) |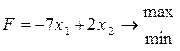
| |
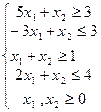
| 21) |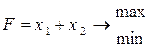 
| 22) | 
| |
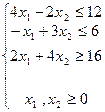
| 23) |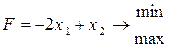 
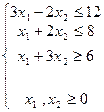
| 24) | 
|
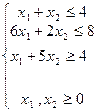
Cимплекс метод
Рассмотрим основную задачу линейного программирования (1.4) - (1.6). Пусть система (1.5) совместна и ее ранг равен r<m.
Выделим базисные и свободные неизвестные и выразим базисные неизвестные через свободные, целевую функцию также выразим через свободные неизвестные.
Пусть х1,х2,...,хк - свободные неизвестные, xk+1,хk+2,..., хn – базисные неизвестные. Тогда
xk+1 = β1 + α'11x1 + … + α'1јxј + … + α'1kxk
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
xk+l = βl + α'l1x1 + … + α'lјxј + … + α'lkxk
- - - - - - - - - - - - - - - - - - - - - - - - - - -
xk+i = βi + α'i1x1 + … + α'iјxj + … + α'ikxk
- - - - - - - - - - - - - - - - - - - - - - - - - - -
xn = βr + α'r1x1 + … + α'rјxj + … + α'rkxk
- - - - - - - - - - - - - - - - - - - - - - - - - - -
F = γ0 + γ'1x1 + … +γ'jxj + …+ γ'kxk.
Пусть все свободные члены системы βl 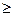0 (l = 
).
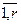Полагаем все свободные неизвестные равными нулю,
т.е. x1 = x2 =…= xk =0.
Тогда базисные неизвестные xk+l = βl (l = 1,2, …, r) и форма F = γ0.
Рассмотрим вопрос об увеличении формы F.
Если все свободные неизвестные х1, x2,..., xk в выражении для F входят с неположительными коэффициентами γ'j 
0 (j = 1, 2,..., k), увеличить форму нельзя, и выбранное решение xj =0 (j = 1, 2, …, k), xk+l = βl (l = 1, 2, …, r) является оптимальным, причем Fmax = γ0.
Предположим теперь, что некоторые γ'j > 0. В этом случае F можно увеличить за счет увеличения свободной неизвестной xj.
Будем увеличивать xj, оставив остальные свободные неизвестные равными нулю. При этом будем иметь:
хk+l = βl + α'lјxј
(l = 1, 2, …, r)
При увеличении хj те базисные неизвестные, для которых α'lј <0 могут только увеличиваться. Если же α'lј <0, при увеличении xj базисная неизвестная xk+l уменьшается, при некотором значении x она становится равной нулю, а затем меньше нуля, нарушая допустимость решения.
Поэтому увеличивать xj. можно лишь до тех пор, пока какая-нибудь базисная неизвестная не обратится в нуль. Пусть это будет xk+i, для которой α'lј <0 и
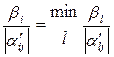
Переведем обратившуюся в нуль базисную неизвестную хk+i в число свободных, а свободную xj – в число базисных.
Снова анализируем форму. Если среди коэффициентов формы нет положительных- достигнут максимум. В противном случае следует повторить изложенную процедуру.
Симплекс метод основан на переходе от одного опорного плана к другому.
Пример. Максимизировать линейную форму F = —х4+ х5 при ограничениях:
x1 + x4 - 2x5 = 1
x2 - 2x4 + x5 = 2
x3 + 3x4 + x5 = 3
Данная система уравнений-ограничений совместна, так как ранги матрицы системы
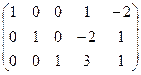
и расширенной матрицы
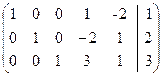
Cовпадают и равны 3. Следовательно, система уравнений совместна и три переменные (базисные) можно линейно выразить через две свободные переменные
x1 = 1 - x4 + 2x5
x2 = 2 + 2x4 - x5
x3 = 3 - 3x4 - x5
Линейную форму выражаем через свободные переменные x4 и x5. (В данном примере уже выражена).
Положив x4 = 0, x5 = 0, найдем значения базисных переменных: x1 =1, x2 =2, x3= 3. Таким образом, первое допустимое решение (1, 2, 3, 0, 0). При этом F1 =0.
Увеличим F1 за счет х5, х5 можно увеличить до 2. Таким образом получим следующее решение (5, 0, 1,0, 2). При этом F2 =2.
Далее примем за свободные переменные х2, x4, то есть переменные, которые в новом решении имеют нулевые значения.
Тогда
x1 = 5 - 2x2 + 3x4
x3 = 1 + x2 +5 x4
x5 =2 - 3x2 + x4
F2=2 - x2 + x4
Будем увеличивать x4, x4 можно увеличить до 1/5.
При этом допустимое решение (23/5, О, О, 1/5, 12/5); F3=11/5
Выразим x1, x4, x5, через свободные переменные x2 и x3:
x1 = 28/5 -3/5x3 - 7/5x2
x4 = 1/5 - 1/5x3 + 1/5x2
x5 = 12/5 - 2/5x3 - 4/5x2
F = 11/5 - 1/5x4 - 4/5x2
Так как в последней линейной форме обе свободные переменные входят с отрицательными элементами, то решение (28/5, О, О, 1/5, 12/5) является оптимальным и Fmax = 11/5.