Постановка задачи
Каждой задаче линейного программирования можно поставить в соответствие другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой:
Прямая:
F(x)=c1x1+ c2x2+…+ cnxn→max
a11x1+ a12x1+…+ a1nxn≤b1,
a21x1+ a22x1+…+ a2nxn≤b2,
………………………………
ak1x1+ ak2x1+…+ aknxn≤bk,
ak+1,1x1+ ak+1,2x1+…+ ak+1,nxn=bk+1,
………………………………
am1x1+ am2x1+…+ amnxn=bm,
Двойственная:
F*(Y)=b1y1+ b2y2+…+ bmym→min
a11y1+ a21y2+…+ am1ym≥c1,
a12y1+ a22y2+…+ am2ym≥c2,
………………………………
a1ly1+ a2ly1+…+ amlym≤cl,
a1,l+1y1+ a2,l+1y2+…+ am,l+1ym=cl+1,
………………………………
a1ny1+ a2ny1+…+ amnym=cm,
Двойственная задача по отношению к исходной составляется согласно правилам:
1. Целевая функция исходной задачи задается на максимум, а двойственной на минимум.
2. Матрица из коэффициентов при неизвестных исходной задачи и аналогичная матрица двойственной задачи получаются друг из друга транспонированием.
3. Число переменных в двойственной задаче равно числу соотношений в системе ограничений исходной задачи, а число ограничений двойственной задачи - числу переменных в исходной задаче.
4. Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе исходной задачи, а правыми частями в системе ограничений двойственной задачи - коэффициенты при неизвестных в целевой функции исходной задачи.
5. Если переменная хj исходной задачи может принимать только лишь положительные значения, то j- e условие в системе ограничений двойственной задачи является неравенством вида " ≥ ". Если же переменная хj может принимать и отрицательные значения, то j -e соотношение в двойственной задаче будет равенством. Если i -e соотношение в исходной задаче является неравенством, то і- я переменная двойственной задачи yi≥0. В противном случае yi может принимать как положительные, так и отрицательные значения.
Двойственные пары задач подразделяются на симметричные и несимметричные. В симметричной паре двойственных задач ограничения прямой и двойственной задач могут принимать лишь неотрицательные значения.
Связь между решениями прямой и двойственной задач.
Если основная задача линейного программирования имеет оптимальный план Х*, то Y*= Cδ . 
является оптимальным планом двойственной задачи. Здесь Cδ - вектор-строка коэффициентов целевой функции при базисных переменных оптимальной симплекс-таблицы прямой задачи, а - матрица обратная матрице, составленной из компонентов векторов, входящих в последний базис, при котором получен оптимальный план. Если прямая задача приведена к единичному базису при неотрицательных свободных членах уравнений, вычисление обратной матрицы не требуется, так как будет состоять из столбцов оптимальной симлекс-таблицы, полученных на месте единичных столбцов исходной таблицы.
Пример 1.
Задана прямая задача:
х1, х2≥0
Составить двойственную задачу.
Решение:
Прежде всего третье ограничение умножим на "-1", так как оно имеет знак «≥». Это ограничение примет вид
-5х1+3х2-6х3≤-19
Матрица из коэффициентов при неизвестных в ограничениях будет:
Запишем транспонированную к ней матрицу:
Тогда двойственная задача запишется:
у1, у3≥0
Так как в прямой задаче второе ограничение имеет знак "=", то переменная y2 не имеет ограничения на знак. Третье ограничение двойственной задачи имеет знак "=" так как переменная х3 не имеет ограничения на знак.
Пример 2.
Прямая задача
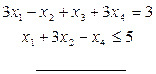
х1, х4≥0
Двойственная задача
| Баз. вект | Сбаз | А0 | ||||||
| А1 | А2 | А3 | А4 | А5 | ||||
| А3 | -1 | |||||||
| ← | А5 | -1 | ||||||
| ∆ | -1 | -5 | -3 | |||||
| ↑ |
| Баз. вект | Сбаз | А0 | ||||||
| А1 | А2 | А3 | А4 | А5 | ||||
| ← | А3 | 14/3 | 10/3 | 8/3 | 1/3 | |||
| А2 | 5/3 | 1/3 | -1/3 | 1/3 | ||||
| ∆ | 34/3 | 5/3 | -14/3 | 5/3 | ||||
| ↑ |
↑
| Баз. вект | Сбаз | А0 | |||||
| А1 | А2 | А3 | А4 | А5 | |||
| А4 | 7/4 | 5/4 | 3/8 | 1/8 | |||
| А2 | 9/4 | 3/4 | 1/8 | 3/8 | |||
| ∆ | 78/4 | 15/2 | 7/4 | 9/4 |
Из последней таблицы получим оптимальный план:
Хопт=(0, 9/4, 0, 7/4);
Данные этой же таблицы используются для определения оптимального решения двойственной задачи.
Вектор Сопт=(С4, С2)=(6,4). Матрица Ах состоит из векторов А4А2, взятых из ограничений по которым составляется двойственная задача:
Ах=(А4А2)= 
Обратная матрица будет:
Тогда: 
Fmin = 
Примечание: Так как исходная задача приведена к единичному базису при неотрицательных свободных членах уравнений, то обратная матрица Ах-1 состоит из компонентов векторов А3 и А5 последней симплекс- таблицы.
3. Варианты заданий
К данной задаче составить сопряженную, решить одну из них и по найденному решению получить решение второй.
| 1) | F=x1+x2→max
| 2) | F=3x1+x2→min
| |
| 3) | F=3x1+3x2→min
| 4) | F=6x1-5x2→max
| |
| 5) | F=8x1+2x2→max
| 6) | F=x1+2x2→max
| |
| 7) | F=14x1+10x2+14x3+14x4→max
| 8) | F=2x1+3x2→min
| |
| 9) | F=5x1+4x2+6x3→max
| 10) | F=-7x1+2x2→min
| |
| 11) | F=6x1+4x2→min
| 12) | F=-x1-2x2→min
| |
| 13) | F=3x1+3x2→max
| 14) | F=-2x1-x2→min
| |
| 15) | F=7x1-2x2→max
| 16)0) | F=3x1+x2+2x3→max
| |
| 17)0) | F=6x1-x2→min
| 18) | F=-3x1-2x2→max
| |
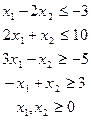
| 19) | F=2x1+x2-3x3→max
| 20) | F=2x1+x2-3x3→max
| |
| 21) | F=x1+2x2→max
| 22) | F=3x1-2x2+x3→max
| |
| 23) | F=5x1-2x2→max
| 24) | F=5x1-2x2→max
| |
| 25) | F=3x1+3x2→max
| 26) | F=5x1+6x2-2x3+3x4→min
| |
| 27) | F=4x1-4x2-4x3+3x4+3x5→min
| 28) | F=3x1+42x2+6x3-4x4→min
|