Симплекс-метод основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает.
Рассмотри расширенную форму ОЗЛП (1.4)-(1.6). Систему уравнений (1.5) запишем в векторной форме
x1P1 + x2P2 + … + xnPn + xn+1Pn+1 + …+ xn+mPn+m = P0 (1.8)
; 
; 
; 
; 
; 
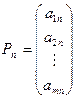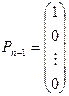В качестве опорного выбирается план x =(0; 0;... 0; b1; b2;...; bm), определяемый системой единичных векторов Pn+1, Pn+2, …, Pn+m, которые образуют базис m -мерного пространства.
Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, составив симплексную таблицу 1.1.
Таблица 1.1
| i | Базис | Сб | ро | С1 | С2 | … | Сr | … | Сn | Cn+1 | … | Се | … | C n+m |
| P1 | P2 | … | Pr | … | Pn | Pn+1 | … | Pе | … | P n+m | ||||
| 1 | Pn+1 | Cn+1 | b1 | a11 | a12 | … | a1r | … | a1n | 1 | … | 0 | … | 0 |
| 2 | Pn+2 | Cn+2 | b2 | a21 | a22 | … | a2r | … | a1n | 0 | … | 1 | … | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| r | Pn+r | Cn+r | br | ar1 | ar2 | … | arr | … | arn | 0 | … | 1 | … | 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| m | Pn+m | Cn+m | bm | am1 | am2 | … | amr | … | amn | 0 | … | 0 | … | 1 |
| m+1 | F0 | ∆1 | ∆2 | ∆r | ∆n | ∆n+1 | … | ∆e | … | ∆n+m |
В столбце Сб той таблицы записываются коэффициенты при неизвестных целевой функции, имеющей те же индексы, что и векторы данного базиса.
В столбце Р0 записываются положительные компоненты исходного плана. В нем же в результате вычислений получают положительные компоненты оптимального плана.
Первые m строк определяются исходными данными задачи, а показатели (т+1)-й строки вычисляют.
f0 - значение целевой функции, которое она принимает при данном опорном плане.
(1.9)
После заполнения таблицы исходный опорный план проверяют на оптимальность. Здесь возможен один из трех случаев:
1. Если все 
неотрицательные, то и найденный опорный план оптимален.
2. <0 для некоторого j, и все соответствующие этому индексу
величины aij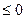 
(i= 
). В этом случае целевая функция не ограничена сверху на множестве планов, поэтому задача неразрешима.
3. <0 для некоторых индексов j, и для каждого такого по крайней мере одно из чисел аij положительно. В этом случае можно перейти от исходного плана к опорному плану, при котором значение целевой функции увеличивается.
Переход от одного опорного плана к другому осуществляется выводом из исходного базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вектора, вводимого в базис, можно взять любой из векторов Рj, для которого <0.
Для определенности выбираем Рj с наибольшим по абсолютной величине отрицательным числом . Пусть это будет при j=k. Тогда в базис вводится вектор Рk..
Для определения вектора подлежащего исключению из базиса, находят min(bi/aik) для всех aik >0. Пусть этот минимум достигается при i=r. Тогда из базиса исключают вектор Рn+г число аrk называют разрешающим элементом.
Столбец и строку, на пересечении которых находится разрешающий элемент, называют направляющими. После выделения направляющей строки и направляющего столбца находят новый опорный план,
компоненты которого вычисляются по формулам:
b'i = 
(1.10)
и коэффициенты a'ij = 
(1.11)
После этого составляют новую симплексную таблицу и вычисляют элементы (m+1)- й строки F'0 и Δj´ по формулам (1.9), в которых все элементы берутся из новой таблицы. Полученный новый опорный план проверяется на оптимальность по знакам Δj. Процесс составления новых планов продолжается до получения оптимального плана или до выяснения неразрешимости задачи.
Пример. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общего количества сырья каждого вида, которое может быть использовано предприятием, приведены в таблице 1.2.
Таблица 1.2.
| Вид сырья | Нормы затрат сырья, кг | Общее кол-во сырья, кг | ||
| А | В | С | ||
| I | ||||
| II | ||||
| III | ||||
| Цена одного изд. |
Изделия А, В и С могут производиться в любых отношениях, но производство ограничено выделенным предприятию сырьем для каждого вида.
Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.
Решение. Обозначим искомый выпуск изделий А через х1, изделий В через х2, изделий С через х3.
Переменные х1, х2, х3 должны удовлетворять следующей системе неравенств (ввиду ограничений на выделяемый фонд сырья):
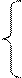18х1 + 15x2+12х3 ≤ 360,
6х1+ 4х2+8x3 ≤ 192, (1.12)
5x1+3х2+3хз ≤ 180.
Общая стоимость произведенной предприятием продукции:
F=9x1 +10x2+16x3 (1.13)
По своему экономическому содержанию переменные х1, х2, х3 могут принимать только лишь неотрицательные значения:
х1, х2, х3 ≥ 0 (1.14)
Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (1.12) требуется найти такое, при котором функция (1.13) принимает максимальное значение.
Перейдем к расширенной форме задачи линейного программирования, введя дополнительные переменные. Получим ограничения в виде равенств
 |
18х1 + 15x2+12х3 + x4 = 360,
6х1+ 4х2+8x3 +x5 = 192,
5x1+3х2+3хз + x6= 180.
Преобразованную систему уравнений запишем в векторной форме:
x1P1+x2P2 + x3P3 + x4P4 + x5P5 + x6P6 =P0,
где
Трехмерные единичные векторы P4, P5, P6 образуют базис трехмерного векторного пространства.
Опорным является план x = (0; 0; 360; 192; 180).
Составляем симплексную таблицу и проверяем исходный план на оптимальность (таблица 1.3).
Таблица 1.3
| i | базис | Сб | Р0 | ||||||
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | ||||
| Р4 | |||||||||
| Р5 | |||||||||
| Р6 | |||||||||
| -9 | -16 |
Значения 4-й строки таблицы подсчитываем по формулам (1.9).
Как видно из таблицы 1.3, значения всех основных переменных х1, х2, х3 равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому "плану", при котором ничего не производится и значение целевой функции равно нулю.
Так как максимальное по абсолютной величине число Δj. стоит в 4-й строке столбца вектора Рз, то в новый базис введем вектор Р3. С экономической точки зрения мы включаем в план производства изделия С.
Определим вектор, подлежащий исключению из базиса. Для этого находим
min (
) для ai3> 0, т.е.
min (
) = 
= 24
т.е. ограничивающим фактором для производства изделий С является имеющийся объем сырья 2-го вида (табл. 1.4). С учетом его наличия предприятие может изготовить 24 изделия С. Следовательно, вектор Р5, подлежит исключению из базиса. Элемент 8, стоящий на пересечении 2-й строки и столбца вектора Р3, является разрешающим. Таким образом, r = 2, k = 3.
Таблица 1.4.
| i | базис | Сб | Р0 | ||||||
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | ||||
| Р4 | -3/2 | ||||||||
| Р3 | 3/4 | 1/2 | 1/8 | ||||||
| Р6 | 11/4 | 3/2 | -3/8 | ||||||
| -2 |
Сначала заполняем строку вектора, вновь введенного в базис, т.е. строку, номер которой совпадает с номером направляющей (2-й) строки. Элементы этой строки получаются из соответствующих элементов предыдущей таблицы делением их на разрешающий элемент. При этом в столбце Cб записываем коэффициент Сз =16, стоящий в столбце вводимого в базис вектора Р3. Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.
Остальные элементы таблицы 1.4 вычисляют по формулам (1.10), (1.11).
По окончании всех расчетов элементов таблицы 1.4 в ней получен новый опорный план: х = (0; 0; 24; 72; 0; 108), который тоже не является оптимальным, поскольку в столбце вектора P2 этой строки стоит отрицательное число -2. Значит, в базис следует ввести вектор Р2, т.е. в новом плане предусмотреть выпуск изделий В.
Для нахождения вектора подлежащего исключению, определяем
min (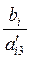
) для a'ir> 0, т.е.
min (
) = 
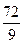= 8
Следовательно, исключению из базиса подлежит вектор Р4. Столбец вектора Р2 и 1-я строка являются направляющими, а число 9 - разрешающий элемент. Отсюда следует, что r = l, k=2.
Составляем таблицу для III итерации (таблица 1.5).
Таблица 1.5
| i | базис | Сб | Р0 | 9 | 10 | 16 | 0 | 0 | 0 |
| Р1 | Р2 | Р3 | Р4 | Р5 | Р6 | ||||
| Р2 | 1/9 | -1/6 | |||||||
| Р3 | 1/4 | -1/18 | 5/24 | ||||||
| Р6 | 5/4 | -1/6 | -1/8 | ||||||
| 2/9 | 5/3 |
В таблице 1.5 сначала заполняем элементы 1-й строки, которая представляет собой строку вновь вводимого в базис вектора Р2. Элементы этой строки получаем из элементов 1-й строки таблицы 1.4 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце Сб данной строки записываем С2=10.
Затем заполняем элементы столбцов вектора базиса и по формулам (3.10), (3.11) вычисляем элементы остальных столбцов. В результате получаем новый план х = (0; 8; 20; 0; 0; 96) и соответствующие значения Δ"j и F0". Среди чисел Δ"j нет отрицательных. Это означает, что найденный опорный план является оптимальным и Fmax =400.
Следовательно оптимальный план включает в себя изготовление 8 изделий В, 20 изделий С и не предусматривает изготовление изделий вида А. При данном плане полностью используется сырье 1 и 2-го видов и остается неиспользованным 96 кг. сырья 3-го вида. Стоимость произведенной продукции равна 400 руб.
Варианты заданий
В задачах 1-25 найти maxF при указанных ограничениях:
| 1) | F=3x1+2x2-6x3
xi≥0; (i=  )
| 2) | F=2x1+3x2-x3
xi≥0; (i= )
| |
| 3) | F=8x1+7x2+x3
xi≥0; (i= )
| 4) | F=x1+3x2-5x3
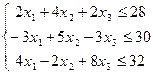xi≥0; (i= )
| |
| 5) | F=x1+2x2-x3
x1, x2, x3≥0
| 6) | F=x1+2x5-5x6
xi≥0; (i=  )
| |
| 7) | F=8x1-3x2+x3+6x4-5x5
xi≥0; (i=1,5)
| 8) | F=2x1-3x2+4x3+5x4-x5+8x6
xi≥0; (i= )
| |
| 9) | F=-3x1+5x2-3x3+x4-x5+8x6
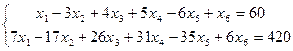xi≥0; (i= )
| 10) | F=5x1-x2+8x3+10x4-5x5+x6
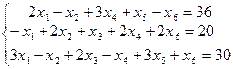xi≥0; (i= )
| |
| 11) | F=10x1+14x2+12x3
xi≥0; (i= )
| 12) | F=4x1+x2-4x3
xi≥0; (i= )
| |
| 13) | F=x1-2x2+5x3
xi≥0; (i= )
| 14) | F=3x1-3x2-4x3
xi≥0; (i= )
| |
| 15) | F=6x1-x2+3x3
xi≥0; (i= )
| 16)0) | F=-2x1-5x2-4x3
xi≥0; (i= )
| |
| 17)0) | F=-3x1+4x2-6x3
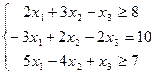xi≥0; (i= )
| 18) | F=x1+2x2-x3
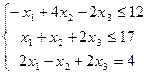xi≥0; (i= )
| |
| 19) | F=10x1+14x2+12x3
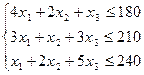xi≥0; (i= )
| 20) | F=9x1+6x2+4x3+7x4
xi≥0; (i=  )
| |
| 21) | F=3x1-7x2-4x4
xi≥0; (i= )
| 22) | F=x1+3x2-5x4
xi≥0; (i= )
| |
| 23) | F=27x1+10x2+15x3+28x4
xi≥0; (i=  )
| 24) | F=3x1+2x2-6x3
xi≥0; (i= )
| |
| 25) | F=3x1+2x5-5x6
xi≥0; (i=  )
|