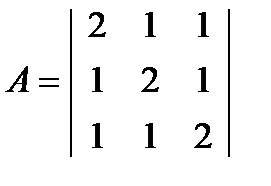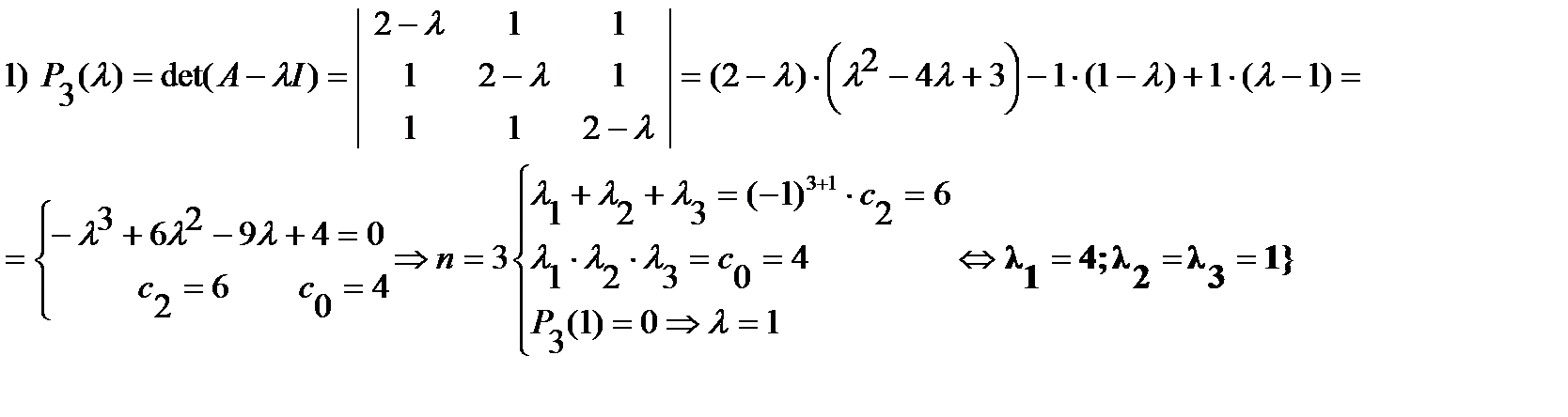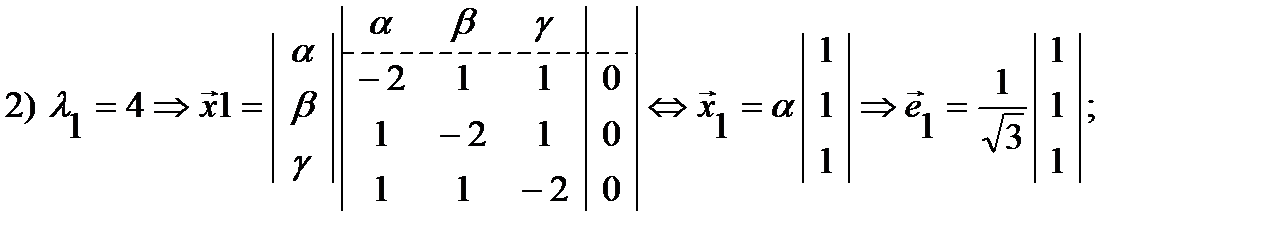Собственные значения вещественной симметричной матрицы.

Собственные значения квадратной матрицы.

Пусть A_n квадратная матрица и X_n - вектор. Очевидно, что матрица A_n отображаетвектор 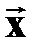в вектор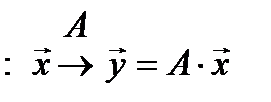

Например,

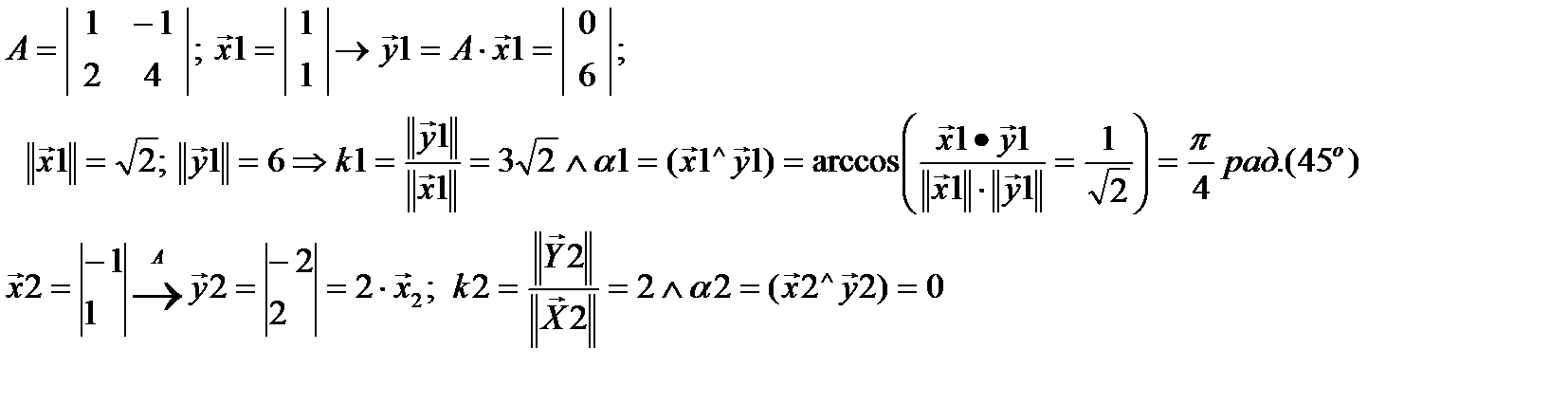
α1

y1

X1

X2

Y2

В общем случае, отображению 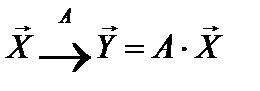соответствуют два геометрических преобразования вектора:

" поворот" на угол α и " растяжения " с коэффициентом растяжения k=||Y|| / ||X||.

Однако, для матрицы А_n существуют "особенные векторы", которые отображаются матрицей в коллинеарные векторы:

 

Известно, что:
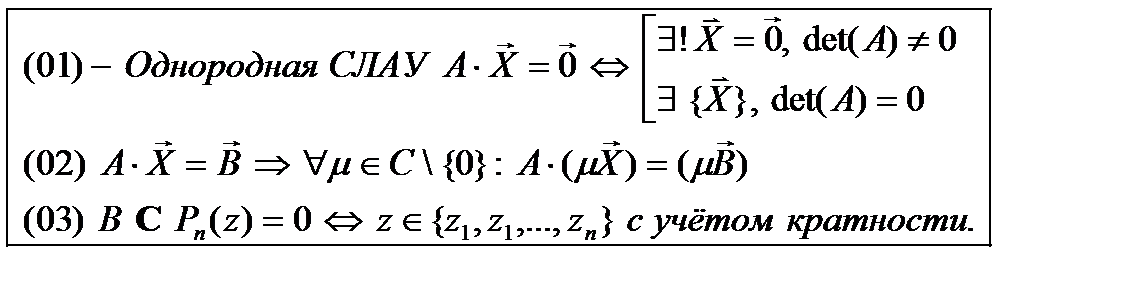(0)

Определение Ч исло λ ÎС(R) и ненулевой вектор X_λ≠0 называются собственными значениями квадратной матрицы А_n (собственным числом λ и соответствующим ему собственным вектором X_λ матрицы ), если они удовлетворяют уравнению

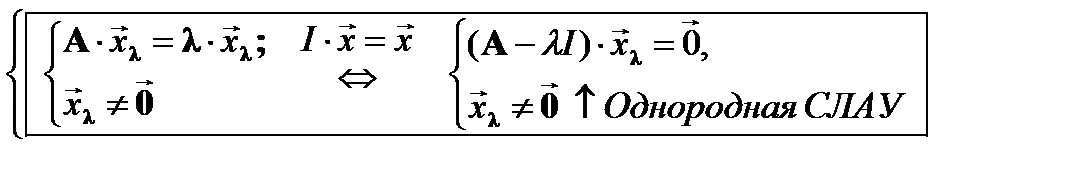(1)

è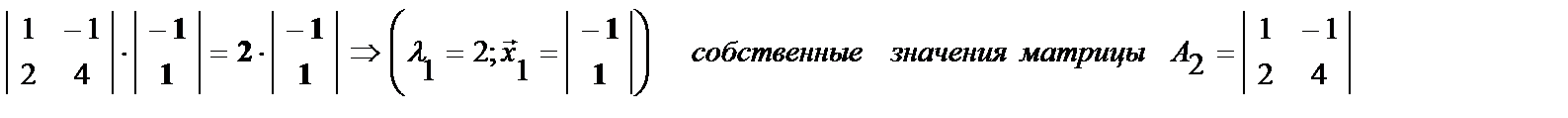

ЭКЗ-9. Доказать, что V1=[1,-1,1]^t и V2=[-3,3,-3]^t - собственные векторы матрицы 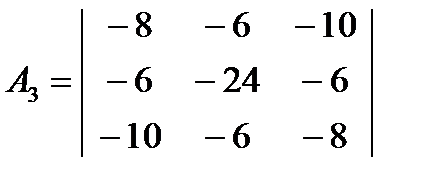. Каким собственным числам они соответствуют?

(1) è 1) ∀A_n∃ (λ,x_λ)? →2) С колько ∃ λ?,x_λ? →3) Как найти множество {(λ,x_λ)}?

 

Ответы следуют из определения (1) и теоремы Крамера (03) для Однородной СЛАУ:

Следствия ( Общие свойства собственных значений матрицы ).

1. Из (1) и (01) следует, что матрица A_n имеет собственные значения, если det(A – λI_n)=0.

2. {λ_A?} è СОБСТВЕННЫЕ ЧИСЛА матрицы находятся из уравнения

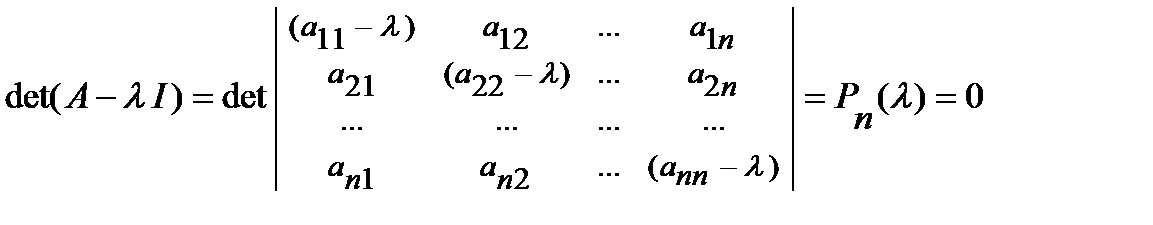, (2)

 

как корни «характеристического полинома 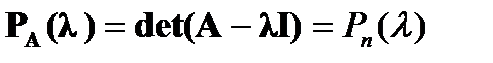матрицы A».
(03) è В С матрица A_n имеет n собственных чисел (с учётом равных (кратных) корней полинома).
(2) è Собственные числа треугольной матрицы равны её диагональным элементам:

 

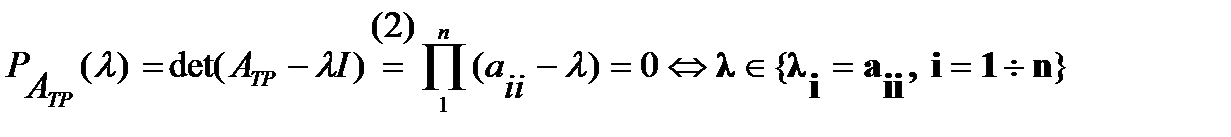
Замечание.

Из представления полинома 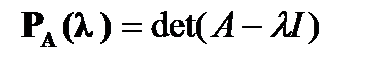в виде суммы степеней 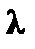и в виде произведения

 

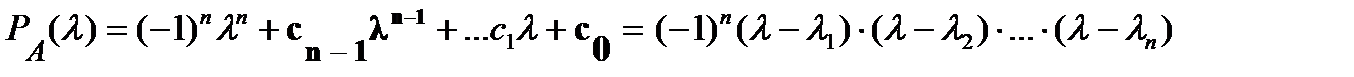
следуют формулы для суммы и произведения собственных чисел матрицы А:

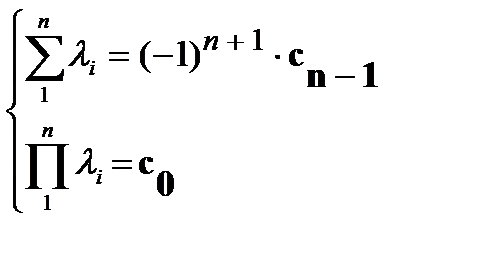
3. {x_λ?} СОБСТВЕННЫЕ ВЕКТОРЫ 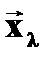, соответствующие собственному числу λ, как ненулевые решения Однородной СЛАУ с вырожденной матрицей

находятся неоднозначно: если 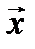- собственный вектор, соответствующий собственному числу λ, то (02)⇒ 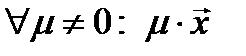- собственный вектор, соответствующий собственному числу λ.

 

èВ дальнейшем в качестве собственного вектора, соответствующего собственному числу λ, будем рассматривать соответствующий единичный собственный вектор

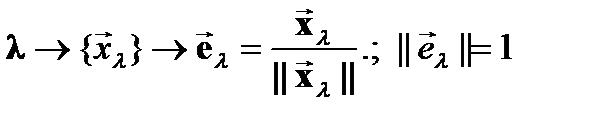
ПРИМЕР

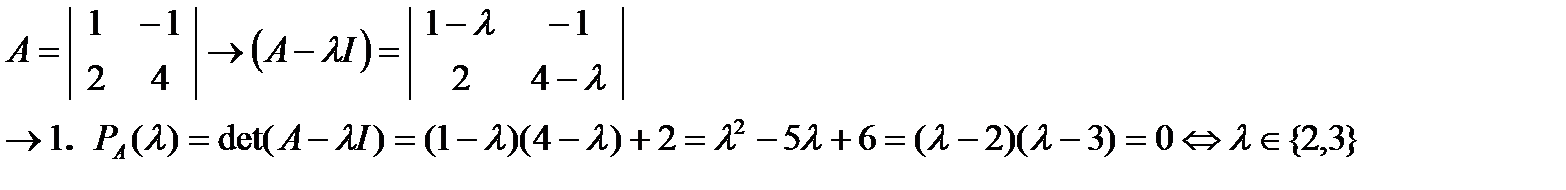
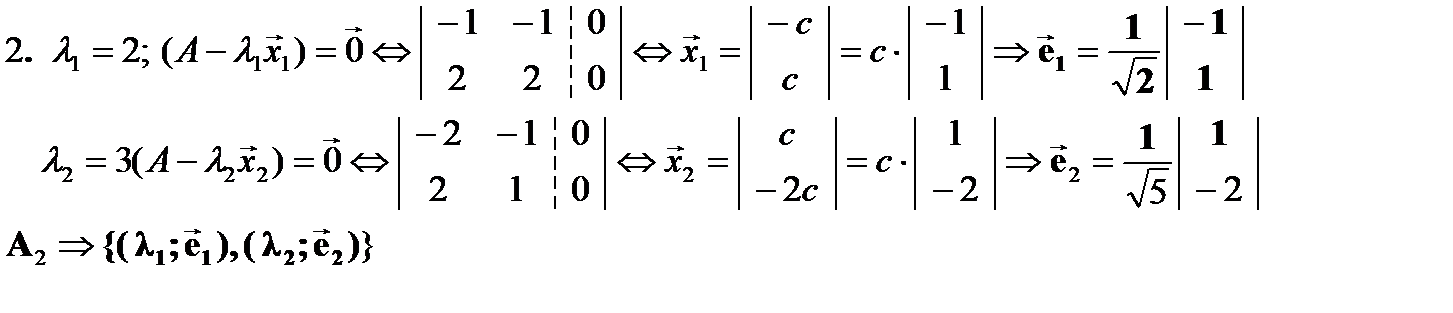
Собственные значения вещественной симметричной матрицы.

Теорема. Если A_n = [a_ik=a_ki∊R]- вещественная симметричная матрица и

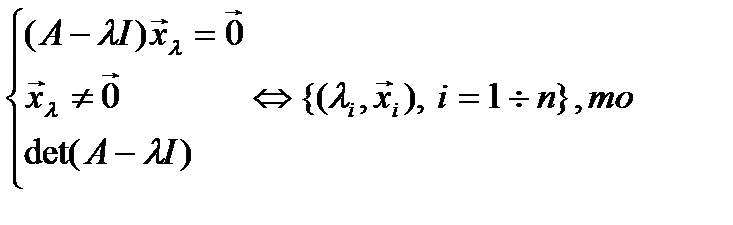
1] Собственные числа матрицы вещественны - λ _i ÎR; i=1:n
2] Собственные векторы, соответствующие различным собственным числам, попарно ортогональны: λ _i ≠ λ_k: (e_{i ∗}e_k)=0.
3] Если матрица A_n имеет "n" различных собственных чисел, то соответствующие единичные собственные векторы матрицы образуют ортонормированный базис ЛВП Rⁿ

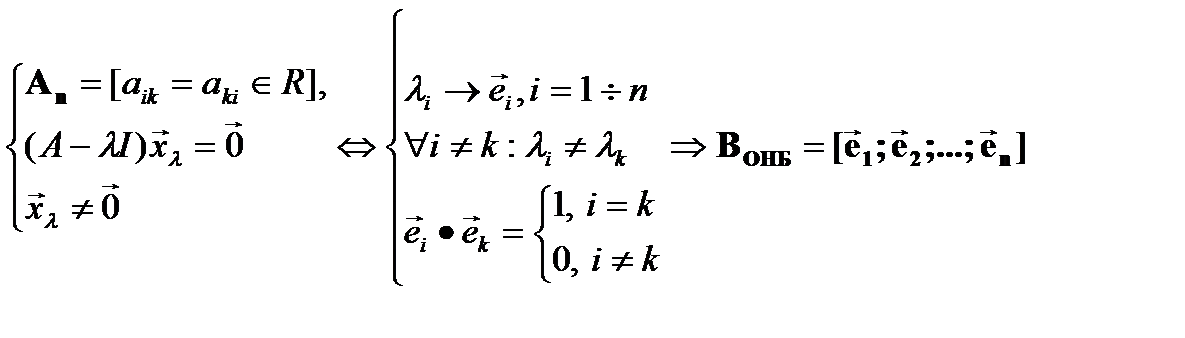
и определяют в Rⁿ (новую) прямоугольную систему координат ;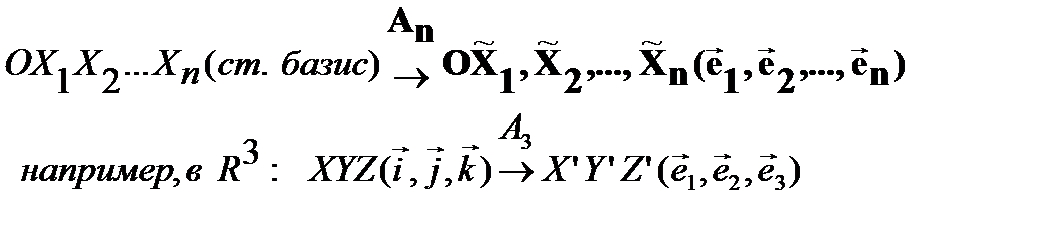

4] Связь координат точки в двух прямоугольных системах координат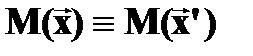
определяется разложениями ее радиус-вектора по соответствующим ОН базисам:

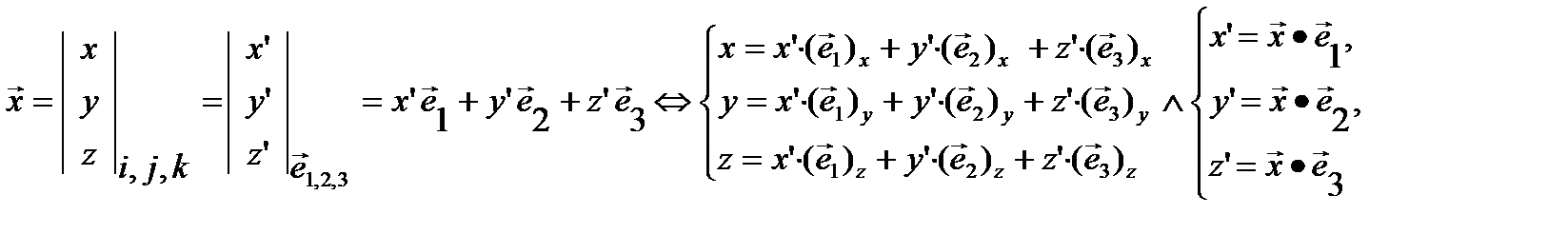
ПРИМЕР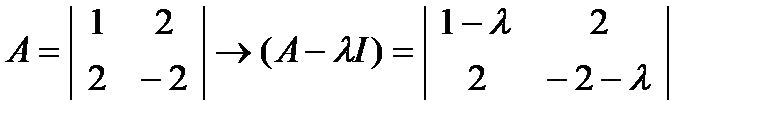

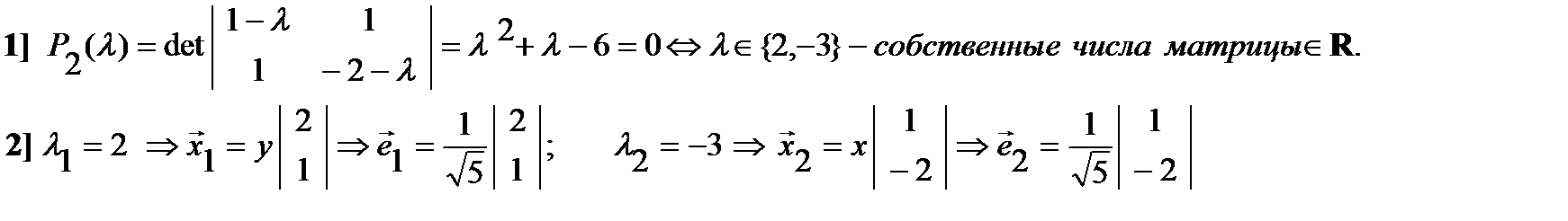
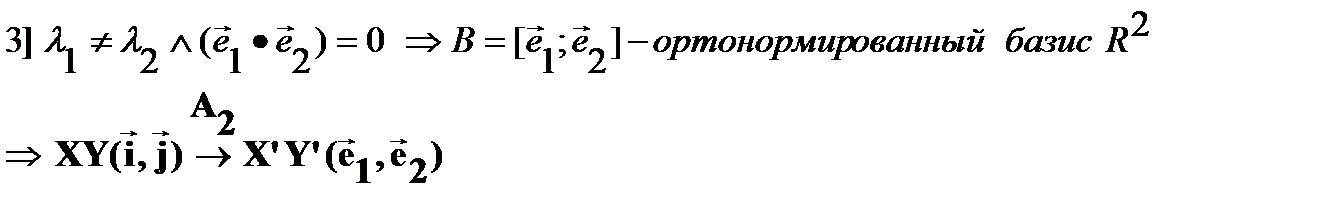
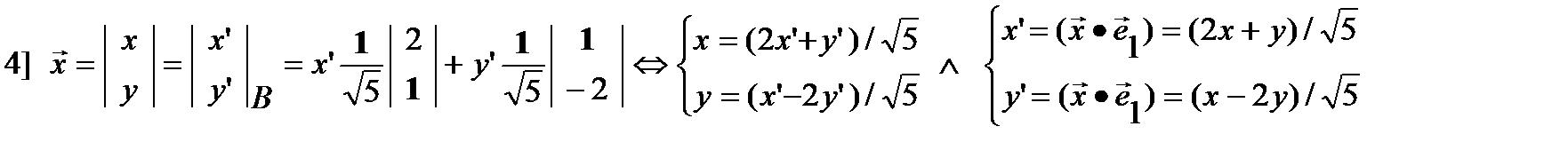
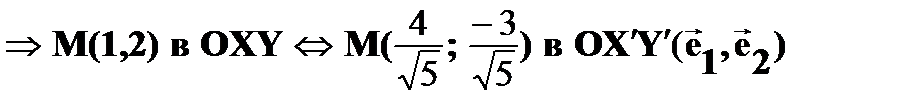
e2

e1

x

y’

x’

y

X’

Y’

X

Y

MM(x’,y’)

M(x,y)

Пример «приложения». Уравнение 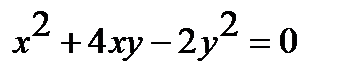в системе координат ОХУ(i,j).

Найдём вид этого уравнения в системе координат ОX’Y’(e₁,e₂).

 

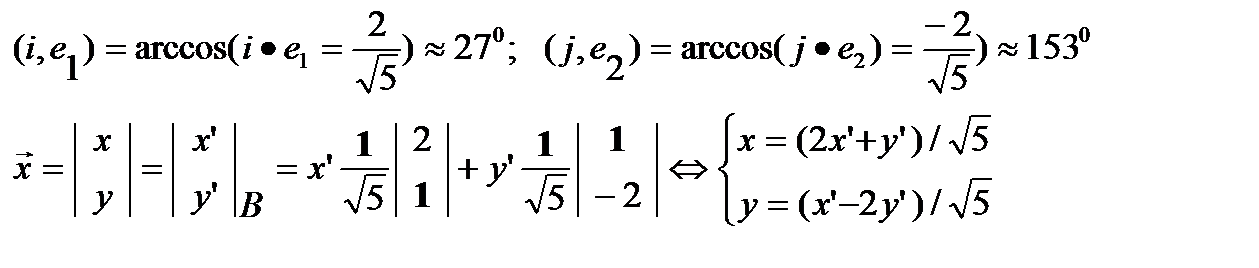
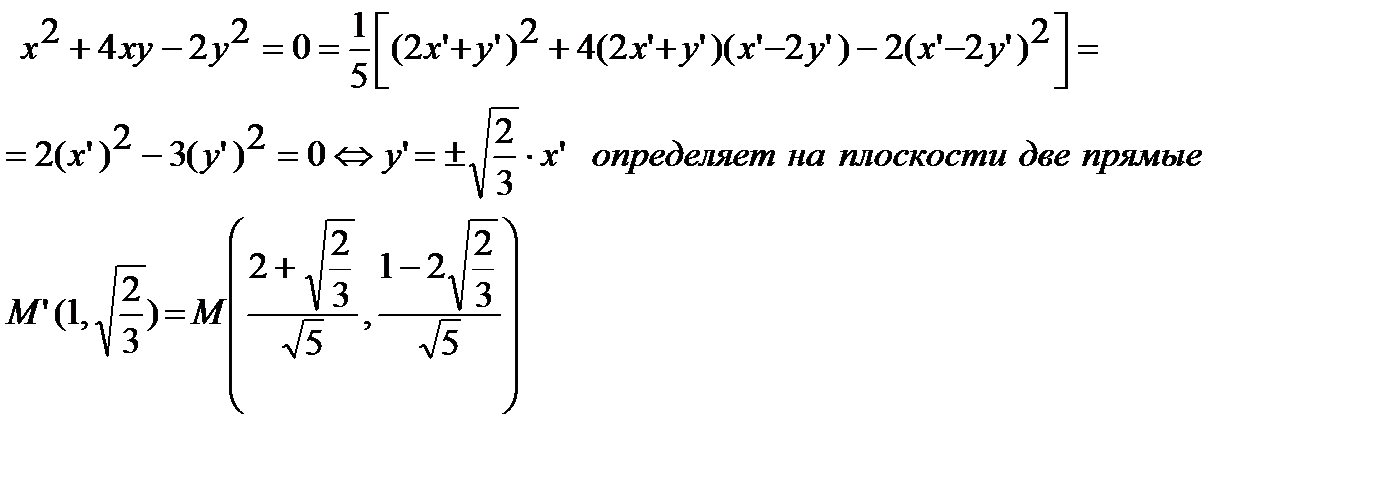
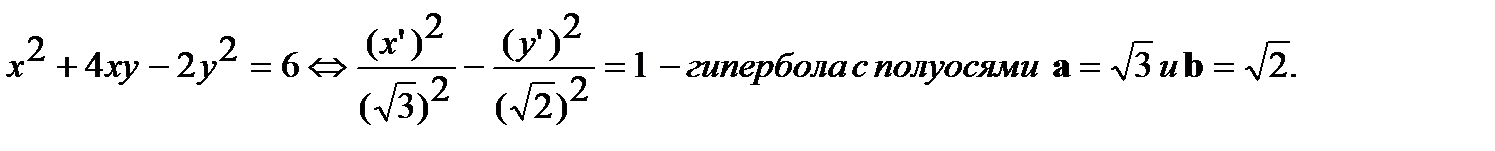
-b

b\b

-a

a

--------------------------------------------------------------------------------------

Замечание. Если матрица имеет кратные собственные числа, существуют (можно выбрать для каждого собственного числа) n попарно ортогональных собственных векторов матрицы, образующих ортонормированный базис и определяющих в Rⁿ прямоугольную систему координат.

Пример Найти ортонормированный базис из собственных векторов симметричной матрицы