Как в состав САР, так и в состав ее элементов могут входить элементарные звенья, поведение которых в статике и динамике является стандартным и может быть описано соответствующими математическими зависимостями. Возможно выделить следующие так называемые т и п о в ы е э л е м е н т а р н ы е з в е н ь я, на которые можно расчленить любую САР или ее синтезировать, используя эти звенья:
1 – идеальное звено;
2 – апериодическое звено;
4 – колебательное звено;
5 – интегрирующее звено;
6 – дифференциальное звено;
7 – звено чистого запаздывания.
Идеальное звено. Предполагается, что масса звена нулевая, а жесткость абсолютная. Примером такого звена является рычаг (усилительное звено) или нагруженная силой F (выходная координата y) пружина в результате перемещения ее свободного конца (рис. 5.20, а). Движение звена подчиняется второму закону Ньютона, но в силу поставленных условий для идеального звена уравнение статики и динамики будут одинаковы: y = k•x, где
 и
и 
.
Временная характеристика звена (переходный процесс) показана на рис. 5.20,б. Из-за отсутствия инерционности звена и абсолютной его жесткости входная координата преобразуется в выходную для любого значения времени.
При подаче на вход идеального (безынерционного) звена периодических синусоидальных воздействий с амплитудой А на выходе звена устанавливаются колебания с амплитудой а, для которых независимо от частоты  отношение амплитуд равно коэффициенту статической передачи (усиления) (рис. 5.20, в). По фазе эти колебания совпадают с колебаниями входной координаты, поэтому сдвиг по фазе
отношение амплитуд равно коэффициенту статической передачи (усиления) (рис. 5.20, в). По фазе эти колебания совпадают с колебаниями входной координаты, поэтому сдвиг по фазе  .
.
Зависимость 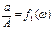 для звена, определенную при изменении частоты колебаний от нуля до бесконечности (
для звена, определенную при изменении частоты колебаний от нуля до бесконечности ( ), называют а м п л и т у д н о - ч а с т о т н о й х а р а к т е р и с т и к о й (А Ч Х).
), называют а м п л и т у д н о - ч а с т о т н о й х а р а к т е р и с т и к о й (А Ч Х).
Для идеального звена 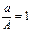 . Зависимость сдвига фаз
. Зависимость сдвига фаз 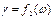 для звена, определенную в диапазоне
для звена, определенную в диапазоне  , называют ф а з о в о й ч а с т о т н о й х а р а к т е р и с т и к о й (Ф Ч Х).
, называют ф а з о в о й ч а с т о т н о й х а р а к т е р и с т и к о й (Ф Ч Х).
Часто применяют понятие амплитудно-фазовая частотная характеристика (АФЧХ), которая одновременно отражает изменение амплитуды и фазовый сдвиг между входной и выходной координатами звена.

Рисунок 5.20. Идеальное звено и его динамические характеристики
Для построения АФЧХ законы синусоидальных колебаний 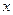 и
и  выражают в векторной форме с помощью комплексно-сопряженных чисел. Синусоидальные колебания представляют в виде изменения проекции вектора на мнимую ось при его вращении против часовой стрелки вокруг начала координат с угловой скоростью
выражают в векторной форме с помощью комплексно-сопряженных чисел. Синусоидальные колебания представляют в виде изменения проекции вектора на мнимую ось при его вращении против часовой стрелки вокруг начала координат с угловой скоростью  , т.е.
, т.е.
 ,
,
 .
.
Отсюда получим  .
.
Таким образом, АФЧХ – это изменение вектора передаточной функции W(iω) при изменении  в диапазоне
в диапазоне 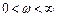 по величине и направлению, конец вектора описывает при этом кривую (годограф).
по величине и направлению, конец вектора описывает при этом кривую (годограф).
Вектор  в общем случае может быть записан как
в общем случае может быть записан как
 .
.
Угол  откладывается против часовой стрелки, если
откладывается против часовой стрелки, если  (запаздывание), или по часовой стрелке, если
(запаздывание), или по часовой стрелке, если 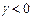 (опережение). В системах автоматического регулирования, как правило, имеет место запаздывание. Величина вектора
(опережение). В системах автоматического регулирования, как правило, имеет место запаздывание. Величина вектора  совпадает с передаточной функцией звена
совпадает с передаточной функцией звена  , если
, если  . Например, если для звена
. Например, если для звена  , то АФЧХ можно представить как
, то АФЧХ можно представить как
 .
.
Для любого идеального (см. рис. 5.20, в) звена АФЧХ вырождается в точку по оси  (здесь откладываются значения
(здесь откладываются значения  ), для любого значения
), для любого значения 
 .
.
Апериодическое звено. Апериодическое звено - самое распространенное
звено в САР. Оно описывается уравнением:
 ,
,
где Т- постоянная времени; у - выходная величина; k - коэффициент усиления;
х - входная величина.
К таким звеньям относятся электрические генераторы, двигатели, электронные и магнитные усилители, проходные четырехполюсники с индуктивностью и емкостью, исполнительные механизмы.
В качестве обобщенного примера рассмотрим звено в виде некоего объема жидкости, ограниченного со всех сторон стенкой, в центре помещен точечный источник энергии 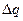 с температурой t0вх. Требуется найти зависимость изменения температуры жидкости t0вых у стенки
с температурой t0вх. Требуется найти зависимость изменения температуры жидкости t0вых у стенки
Таким образом, это аналог системы охлаждения двигателя. Источник энергии – рабочий процесс в цилиндре со средней интегральной температурой в объеме сгорающей топливовоздушной смеси (рис. 5.21).
Подведенное тепло идет на аккумулирование энергии  в объеме жидкости, связанной с повышением температуры, и часть энергии рассеивается (диссипирует) в окружающей объем среде
в объеме жидкости, связанной с повышением температуры, и часть энергии рассеивается (диссипирует) в окружающей объем среде  . Уравнение баланса энергии
. Уравнение баланса энергии  . Если рассматривать процесс в интервале времени
. Если рассматривать процесс в интервале времени  , стремящемся к нулю, то уравнение запишется как
, стремящемся к нулю, то уравнение запишется как
 .
.
С целью упрощения задачи будем считать, что вследствие теплоизоляции стенок диссипация энергии отсутствует и 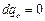 . Используя простейшие зависимости тепловой физики, определим
. Используя простейшие зависимости тепловой физики, определим  и
и  как
как
 и
и 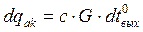 ,
,
где  - коэффициент теплопередачи от источника энергии в жидкость;
- коэффициент теплопередачи от источника энергии в жидкость;
 -среднеинтегральная площадь теплопередачи;
-среднеинтегральная площадь теплопередачи;
 -теплоемкость жидкости;
-теплоемкость жидкости;
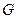 -масса жидкости в объеме.
-масса жидкости в объеме.
Раскроем уравнение баланса энергии

или
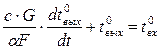 .
.

Рисунок 5.21. Схематичное представление одноемкостного
апериодического звена 1-го порядка
Удобнее производить запись уравнения через приращения переменных, что соответствует переносу начала координат в точку, с которой начинается процесс изменения температуры
 .
.
После введения относительных координат
 и
и 
получим так называемые уравнения движения (динамики) звена
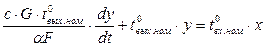
или  ,
,
где  - коэффициент, так называемое время звена;
- коэффициент, так называемое время звена;
 – коэффициент статической передачи (усиления) звена.
– коэффициент статической передачи (усиления) звена.
Часто уравнение движения представляют в ином виде:
 или
или  ,
,
где  – время разгона объекта;
– время разгона объекта;
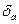 – коэффициент самовыравнивания или коэффициент неравномерности звена.
– коэффициент самовыравнивания или коэффициент неравномерности звена.

Рисунок 5.22. Временная характеристика звена
Коэффициент передачи такого звена в комплексном виде представляет собой уравнение

Передаточная функция

 .
.
Колебательное звено (рис. 5.23) - это звено, в котором при скачкообразном изменении входной величины выходная величина стремится к новому установившемуся значению, совершая затухающие колебания. Его передаточная функция

где ε - степень затухания.
Постоянная времени Т связана с резонансной частотой ω0(Т -1: ω0) и в 2 π раз меньше периода т. е. Т = 1: ω0 = 2 πТ.

Рисунок 5.23. Примеры колебательных звеньев:
а) электрическая схема; б) механическая система; в) временная характеристика.
Интегрирующее звено. Простейшее интегрирующее звено представлено на рис.5.24. Зависимость между входной и выходной координатами определяется уравнением
 .
.

Рисунок 5.24. Переходный процесс интегрирующего звена
и его характеристики
Переходный процесс интегрирующего звена и его характеристики приведены на рис.5.24. Так, при «скачкообразном» возмущении, например, при 

 .
.

Отклонение выходной величины пропорционально интегралу отклонения входной координаты  , поэтому такие звенья называют интегрирующими.
, поэтому такие звенья называют интегрирующими.
Передаточную функцию интегрирующего звена получим из уравнения, записанного в операторной форме
 и
и  .
.
АФЧХ при подстановке в 
 определится при условии
определится при условии 
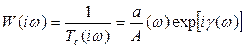 .
.
Выделив  и
и  , получим
, получим 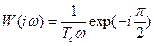 .
.
Дифференцирующее звено. В идеальном дифференцирующем звене (см. рис.5.25,а) зависимость между входной и выходной координатами определяется уравнением
 .
.
В операторной форме уравнение движения  .
.
Передаточная функция  , откуда
, откуда



 .
.




 |  |
АФЧХ АЧХ ФЧХ
Уравнение движения дифференцирующего звена показывает, что при «ступенчатом» возмущении (см. рис.5.25, б) переходный процесс начинается мгновенным импульсом бесконечной (теоретически) амплитуды. Но так как длительность времени изменения входной координаты стремится к нулю, то сразу же за установлением  выходная координата также принимает нулевое значение
выходная координата также принимает нулевое значение  .
.
Звено состоит из катаракта 1 и пружины 2 (см. рис.5.25, а). В технике такое звено принято называть изодромом. Если через изодром (дифференцирующее звено) проходит обратная связь, то ее называют изодромной или гибкой обратной связью (ГОС).

Рисунок 5.25. Дифференцирующее звено, его переходный процесс и характеристики
Звено чистого запаздывания. Звеном чистого запаздывания называется звено, в котором изменения выходной координаты  полностью повторяют изменения входной координаты
полностью повторяют изменения входной координаты  , но смещены относительно ее во времени, т.е. происходят с некоторым запаздыванием
, но смещены относительно ее во времени, т.е. происходят с некоторым запаздыванием  (рис. 5.26, а).
(рис. 5.26, а).
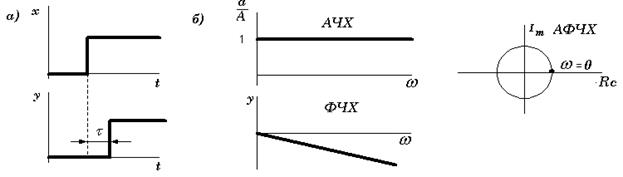
Рисунок 5.26. Переходный процесс звена чистого запаздывания
и его характеристики
Реально такое звено не существует. Путем искусственного введения в цепочку САР звеньев запаздывания удается приблизить их математическое описание к реальным процессам, например, двигателя, можно учесть тепловое и химическое запаздывание между процессом ввода топлива и сгоранием, дискретность топливоподачи, наличие люфтов и зазоров в передаче сигнала от регулятора к топливной аппаратуре и т.п. Зависимость между входной и выходной координатами записывается следующим уравнением:  , где
, где 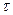 - временное запаздывание.
- временное запаздывание.
Передаточная функция имеет вид
 .
.
Амплитудная фазовая частотная характеристика имеет вид
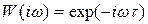 .
.
Переходный процесс звена чистого запаздывания и его характеристики приведены на рис. 5.26.