Любые операции в ЭВМ выполняются над числами, которые представляются специальными двоичными кодами. Применение этих кодов позволило обрабатывать знаковые разряды чисел так же как и значащие разряды, т.е. определять знак результата и переполнение разрядной сетки машины. Благодаря этим кодам, все арифметические операции сводятся к операции сложения.
Различают прямой, обратный и дополнительный коды двоичных чисел, которые используются для представления отрицательных чисел. Положительное число в прямом, обратном и дополнительном кодах не меняет своего изображения.
Прямой код отрицательного числа А(2) = -0, а1 а2... апв форме с фиксированной точкой (запятой) имеет следующее машинное изображение:
(2)
Обратный код имеет следующее важное свойство: сумма положительного числа А с его отрицательным значением в обратном коде дает так называемую машинную единицу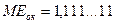 
, которая состоит из единиц как в знаковом, так и в значащих разрядах числа.
Пусть 
- положительное число;
- отрицательное значение числа А(2) в обратном коде.
Сумма 
: (3)
|
Дополнительный код отрицательного числа получают добавлением единицы в самый младший разряд обратного кода числа (20 - для целых чисел, 2-k - для дробных). Основные свойства дополнительного кода:
· сумма дополнительного кода положительного числа А и его отрицательного значения представляет собой машинную единицу дополнительного кода при добавлении единицы к младшему разряду: МЕДК =
= МЕОК + 20 = 10,000...00, т.е. в результате получается число 10(2) = 2(10);
· представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕОК.
Пример:
Дано число А(2) = 1.01011001. Необходимо представить его в прямом, обратном и дополнительном кодах.
Преобразование в обратный код (при записи над цифрой проводится черта, которая указывает на инверсное значение символа):
.
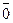
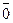
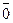
Преобразование в дополнительный код:
+
Все арифметические операции в ЭВМ приводятся к операции сложения. Операция вычитания приводится к операции сложения путем представления отрицательного числа в обратном (или дополнительном) коде. В таблице 2 представлена процедура выполнения операции алгебраического сложения при 
и 
.
Таблица 2 – Преобразование кодов при алгебраическом сложении
| Выполняемая операция | Необходимое преобразование |
| А + В | А + В |
| А - В | А + (- В) |
| - А + В | (- А) + В |
| - А - В | (- А) + (- В) |
Если число указано в скобках, то необходимо заменить операцию вычитания на операцию сложения с обратным или дополнительным кодом числа.
При выполнении операций сложения необходимо выполнять такие правила:
· слагаемые должны иметь равное число разрядов. Для приведения в соответствие слагаемым возможно приписывать незначащие нули к целой части числа слева, а к дробной справа;
· со знаковыми разрядами чисел при сложении выполняются действия, подобные значащим разрядам;
· над приписанными незначащими нулями выполняются все действия по общему правилу;
· сложение в прямом коде выполняется только над числами одного знака. Знак результата соответствует знаку любого операнда (числа);
· числа с разными знаками суммируются в обратном или дополнительных кодах;
· сумма обратных кодов чисел есть обратный код результата;
· если при сложении обратных кодов чисел возникает перенос из знакового разряда, то он добавляется к младшему разряду цифровой части;
· сумма дополнительных кодов есть дополнительный код результата;
· если при сложении дополнительных кодов возникает перенос из знакового разряда, то он отбрасывается,т.е. теряется.
Пример.
Рассмотрим процесс сложения в двоичном коде чисел:
А(10) = 0,51 и В(10) = -0,39.
Представим числа в двоичном коде, пользуясь любым из известных правил преобразования целых чисел:
А(2) = 0,10000 В(2) = -0,01100
Выполним сложение в обратных кодах. Так как число А положительное, то обратный код будет совпадать с его исходным изображением:
[ A ]обр = 0 10000
Для отрицательного числа В обратный код получаем инверсией исходного изображения и записью единицы в знаковый разряд:
[ B ]обр = 1 10011
На следующем этапе находим сумму. Процедуру сложения начинаем с младшего разряда:
[ A ]обр = 0 10000
+
[ B ]обр = 1 10011
_______________
1 0 00011
 |
При сложении возникла единица переноса из знакового разряда, которую необходимо добавить в самый младший разряд цифровой части:
0 00011
+ 1
0 00100
Сложим числа, представленные в дополнительном коде:
[ A ]доп = 0 10000
Преобразуем в дополнительный код число В:
[ B ]доп = [ B ]обр + 1 мл.р. (4)
[ B ]обр = 1 10011
+ 1
[ B ]доп = 1 10100
Выполним операцию сложения дополнительных кодов:
[ A ]доп = 0 10000
+
[ B ]доп = 1 10100
1 0 00100
Возникшая единица переноса отбрасывается. В полученной сумме в дополнительном коде знаковый разряд равен 0, результат также равен положительному числу 0,00100.