14.1. Производная произведения 
равна …
; 
; 
; 
.
14.2. Производная частного 
равна …
; 
; 
; 
.
14.3. Производная частного 
равна …
; 
; 
; 
.
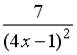14.4. Производная функции 
равна…
; 
; 
; 
.
14.5. Производная функции 
равна…
; 
; 
; 
.
Производные высших порядков.
15.1. Значение производной третьего порядка функции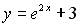 
в точке 
равно:…0; 1; 4; 8.
15.2. Значение производной второго порядка функции 
в точке равно:…- 1; 1; - 25; 25.
15.3. Значение производной второго порядка функции 
в точке 
равно: …0; 6; 9; 1.
15.4. Значение производной второго порядка функции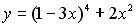 
в точке равно: …16; 108; 12; 112.
15.5. Производная второго порядка функции 
имеет вид…
; 
; 
; 
.
Приложения дифференциального исчисления ФОП.
16.1. Наименьшее значение функции 
на отрезке 
равно …(1).
16.2. Наименьшее значение функции 
на отрезке 
равно …(1).
16.3. Наименьшее значение функции 
на отрезке 
равно (2).
16.4. Наименьшее значение функции 
на отрезке равно …(1).
16.5. Наибольшее значение функции 
на отрезке 
равно …(7).
Дифференциальное исчисление ФНП.
17.1. Частная производная функции 
по переменной 
в точке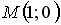 
равна…: 1; 0; 2; 3.
17.2. Частная производная функции 
по переменной 
в точке 
равна…: 
; 
; 
; 
.
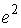17.3. Частная производная функции 
по переменной в точке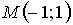 
равна…: – 3; ; 1; 3.
17.4. Линиями уровня функции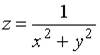 
являются …:
прямые; эллипсы; гиперболы; окружности.
17.5. Линиями уровня функции 
являются …:
эллипсы; гиперболы; параболы; прямые.
Приложения определённого интеграла.
18.1. Площадь фигуры, изображенной на рисунке,
определяется интегралом…
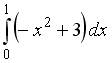
18.2. Площадь фигуры, изображенной на рисунке, определяется интегралом…
18.3. Площадь фигуры, изображенной на рисунке, определяется интегралом…
18.4. Площадь фигуры, изображенной на рисунке, определяется интегралом…
18.5. Площадь фигуры, ограниченной параболой 
и прямой 
:
вычисляется с помощью интеграла …
Типы дифференциальных уравнений.
19.1. Среди перечисленных дифференциальных уравнений уравнениями первого порядка являются:
; 
; 
19.2. Среди перечисленных дифференциальных уравнений уравнениями первого порядка являются:
; 
; 
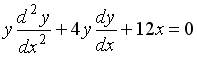
19.3. Среди перечисленных дифференциальных уравнений уравнениями второго порядка являются:
; 
; 
19.4. Среди перечисленных дифференциальных уравнений уравнениями второго порядка являются:
; 
; 
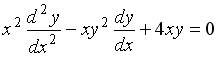
19.5. Из данных дифференциальных уравнений уравнениями Бернулли являются…
; 
; 
ДУ первого порядка.
20.1. Дано дифференциальное уравнение 
. Тогда его решением является функция:… 
; 
; 
; 
.
20.2. Дано дифференциальное уравнение 
. Тогда его решением является функция:…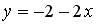 
; 
; 
; 
.
20.3. Дано дифференциальное уравнение 
при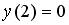 
. Тогда интегральная кривая, которая определяет решение этого уравнения, имеет вид…
A
D
C
B
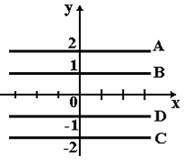20.4. Дано дифференциальное уравнение 
при 
. Тогда интегральная кривая, которая определяет решение этого уравнения, имеет вид…
C
B
D
A
20.5. Общее решение дифференциального уравнения 
имеет вид …
; 
; 
; 
.
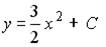ДУ высших порядков.
21.1. Общее решение дифференциального уравнения 
имеет вид …
; 
;
; 
.
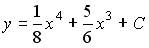21.2. Общее решение дифференциального уравнения 
имеет вид …
; 
;
; 
.
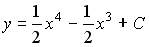21.3. Общее решение дифференциального уравнения 
имеет вид …
; 
;
; 
.
21.4. Общее решение дифференциального уравнения 
имеет вид …
; 
;
; 
.
21.5. Общее решение дифференциального уравнения 
имеет вид …
; 
;
; 
.