ДАС
1.Вычисление определителей.
2.Матрицы, основные понятия и определения.
3.Линейные операции над матрицами.
4.Умножение матриц.
5.Системы линейных уравнений, основные понятия.
6.Системы линейных уравнений, методы решения.
7.Основные задачи аналитической геометрии на плоскости.
8.Прямая на плоскости.
9.Кривые второго порядка.
10.Прямая и плоскость в пространстве.
11.Функции, основные понятия и определения.
12.Предел функции.
13.Геометрический и физический смысл производной.
14.Производные первого порядка.
15.Производные высших порядков.
16.Приложения дифференциального исчисления ФОП.
17.Дифференциальное исчисление ФНП.
18.Приложения определённого интеграла.
19.Типы дифференциальных уравнений.
20.ДУ первого порядка.
21.ДУ высших порядков.
22.Линейные дифференциальные уравнения 2-го порядка.
Вычисление определителей.
1.1. Установите соответствие между матрицей и ее определителем.
1. 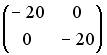 ; 2.
; 2.  ; 3.
; 3. 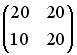
0; 400; - 400; 200; - 200.
1.2. Установите соответствие между  и значениями определителей
и значениями определителей 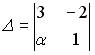 .
.
1.  4 2.
4 2. 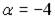 4 3.
4 3. 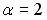 ;4.
;4.  .
.
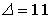 ;
; 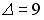 ;
; 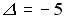 ;
; 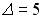 ;
; 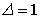 ;
; 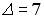 .
.
1.3. Установите соответствие между 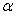 и значениями определителей
и значениями определителей 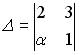 .
.
1.  ; 2.
; 2. 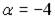 ; 3.
; 3. 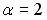 ; 4.
; 4.  .
.
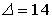 ;
; 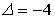 ;
; 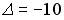 ;
; 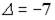 ;
; 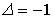 ;
; 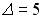 .
.
1.4. Установите соответствие между 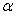 и значениями определителей
и значениями определителей 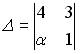 .
.
1.  ; 2.
; 2. 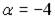 ; 3.
; 3. 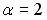 ; 4.
; 4.  .
.
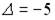 ;
; 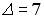 ;
; 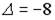 ;
; 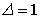 ;
; 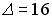 ;
; 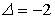 .
.
1.5. Установите соответствие между 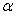 и значениями определителей
и значениями определителей 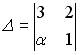 .
.
1.  ; 2.
; 2. 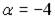 ; 3.
; 3. 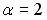 ; 4.
; 4.  .
.
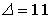 ;
; 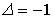 ;
; 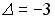 ;
; 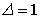 ;
; 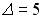 ;
; 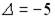 .
.
2.Матрицы, основные понятия и определения.
2.1. Даны матрица 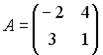 и транспонированная матрица
и транспонированная матрица 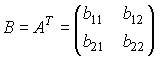 . Установите соответствие между элементами транспонированной матрицы
. Установите соответствие между элементами транспонированной матрицы 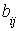 и элементами матрицы А
и элементами матрицы А
1. 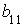 ; 2.
; 2. 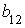 ; 3.
; 3. 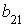 ; 4.
; 4. 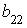 . – 3; - 2; 3; 2; 1; 4.
. – 3; - 2; 3; 2; 1; 4.
2.2. Установите соответствие между матрицами и их рангами.
1)  ; 2)
; 2) 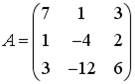 ; 3)
; 3) 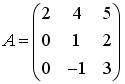 ; 4)
; 4) 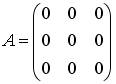 .
.
1; 0; 5; 2; 3; 4.
2.3. Установите соответствие между матрицами и их рангами.
1)  ; 2)
; 2) 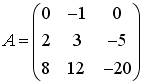 ; 3)
; 3) 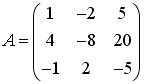 ; 4)
; 4) 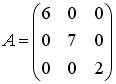
4; 2; 5; 1; 0; 3.
2.4. Установите соответствие между матрицами и их рангами.
1) 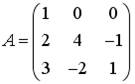 ; 2)
; 2)  ; 3)
; 3) 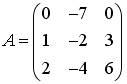 ; 4)
; 4) 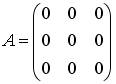
1; 2; 5; 4; 3; 0.
2.5. Дана матрица  . Установите соответствие между указанными элементами и их алгебраическими дополнениями.
. Установите соответствие между указанными элементами и их алгебраическими дополнениями.
1) 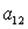 ; 2)
; 2) 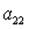 ; 3)
; 3) 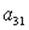 ; 4)
; 4) 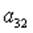 .
.
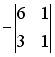 ;
; 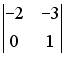 ;
; 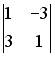 ;
; 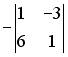 ;
;  ;
;  .
.
Линейные операции над матрицами.
3.1. Даны матрицы 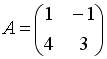 и
и 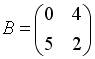 . Тогда решением матричного уравнения
. Тогда решением матричного уравнения 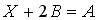 является матрица …
является матрица …
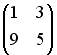 ;
; 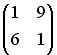 ;
; 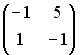 ;
; 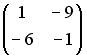 .
.
3.2. Даны матрицы 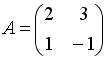 и
и 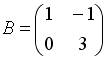 . Тогда решением матричного уравнения
. Тогда решением матричного уравнения 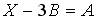 является матрица …
является матрица …
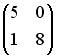 ;
; 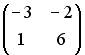 ;
; 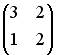 ;
; 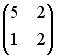 .
.
3.3. Если 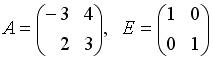 , то значение определителя матрицы
, то значение определителя матрицы 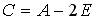 равно …: 3; - 14; - 3; - 13.
равно …: 3; - 14; - 3; - 13.
3.4. Даны матрицы 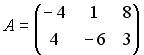 и
и 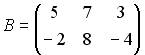 . Тогда матрица
. Тогда матрица 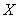 , являющаяся решением уравнения
, являющаяся решением уравнения 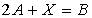 , равна …
, равна …
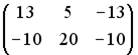 ;
; 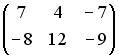 ;
; 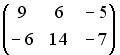 ;
; 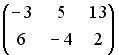 .
.
3.5. Даны матрицы 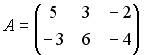 и
и 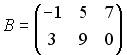 . Тогда матрица
. Тогда матрица 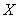 , являющаяся решением уравнения
, являющаяся решением уравнения 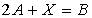 , равна …
, равна …
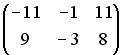 ;
;  ;
; 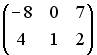 ;
; 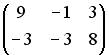 .
.
Умножение матриц.
4.1. Операция произведения матриц правильно определена для матричного умножения вида …
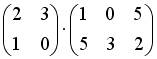 ;
; 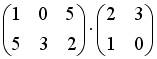 ;
; 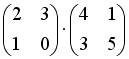 ;
; 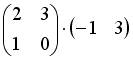
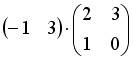
4.2. Операция произведения матриц правильно определена для матричного умножения вида …
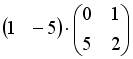 ;
; 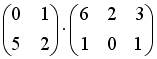 ;
; 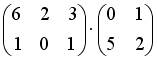 ;
; 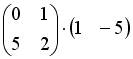
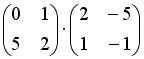
4.3. Для матриц 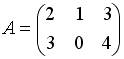 и
и 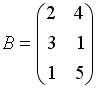 и транспонированных к ним определены произведения …
и транспонированных к ним определены произведения … 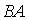 ;
; 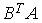 ;
; 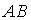 ;
; 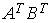 ;
; 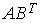
4.4. Для матриц 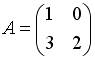 и
и 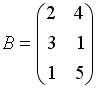 и транспонированных к ним определены произведения …
и транспонированных к ним определены произведения … 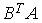 ;
; 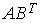 ;
; 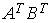 ;
; 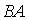 ;
; 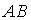
4.5. Для матриц 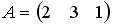 и
и 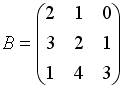 и транспонированных к ним определены произведения …
и транспонированных к ним определены произведения … 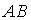 ;
; 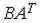 ;
; 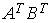 ;
; 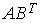 ;
; 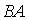
5.Системы линейных уравнений, основные понятия.
5.1. Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. 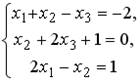 ;2.
;2. 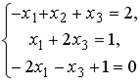 ;3.
;3. 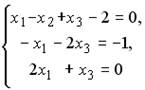 ;4.
;4. 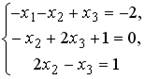
 ;
;  ;
;  ;
;  ;
;  ;
; 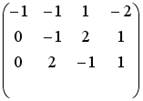 .
.
5.2. Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. 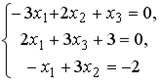 2.
2. 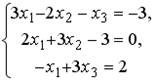 3.
3. 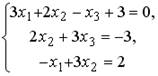 4.
4. 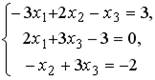
 ;
;  ;
;  ;
;  ;
;
 ;
;  .
.
5.3. Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. 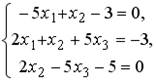 ;2.
;2. 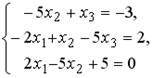 ;3.
;3. 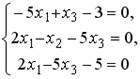 ;4.
;4. 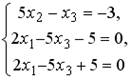
 ;
; 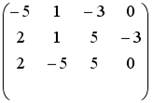 ;
; 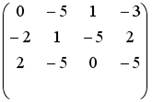 ;
; 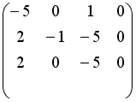 ;
;
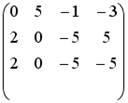 ;
; 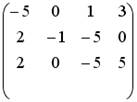 .
.
5.4. Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. 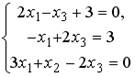 ;2.
;2. 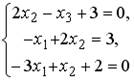 ;3.
;3. 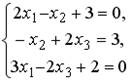 ;4.
;4. 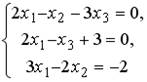
 ;
;  ;
;  ;
;  ;
;
 ;
;  .
.
5.5. Установите соответствие между системой линейных уравнений и ее расширенной матрицей.
1. 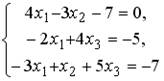 ;2.
;2. 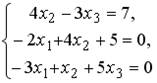 ;3.
;3. 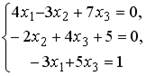 ;4.
;4. 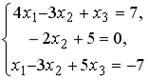
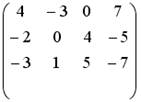 ;
;  ;
;  ;
;  ;
;
 ;
;  .
.
Системы линейных уравнений, методы решения.
6.1. Если 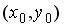 – решение системы линейных уравнений
– решение системы линейных уравнений 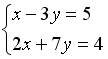 , то
, то 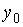 может определяться по формуле…
может определяться по формуле…
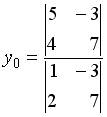 ;
; 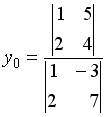 ;
; 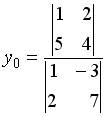 ;
; 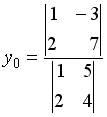 .
.
6.2. Дана система линейных уравнений 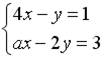 . Система не имеет решений при а равном:…-8; 8; 5; -5.
. Система не имеет решений при а равном:…-8; 8; 5; -5.
6.3. Пусть 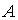 и
и 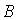 – обратимые квадратные матрицы одного порядка. Тогда решением матричного уравнения
– обратимые квадратные матрицы одного порядка. Тогда решением матричного уравнения 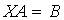 является матрица…
является матрица…
 ;
; 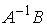 ;
; 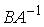 ;
;  .
.
6.4. Система линейных уравнений 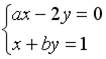 имеет решение
имеет решение 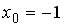 ,
, 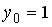 при …
при …
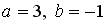 ;
; 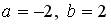 ;
; 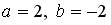 ;
; 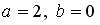 .
.
6.5. Система линейных уравнений 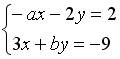 имеет решение
имеет решение 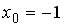 ,
, 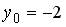 при:
при: 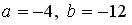 ;
; 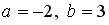 ;
; 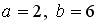 ;
; 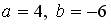 .
.